标签:cpp less tar [] put parallel 意思 const jline
转自http://www.cnblogs.com/xdruid/archive/2012/06/20/2555536.html
这道题算是很好的一道凸包的题吧,做完后会加深对凸包的理解。
题意很关键。。。这英语看了好几遍才差不多看明白了。意思就是给你一堆点,这堆点本来就是某个凸包上的部分点,问你这堆点是否能确定唯一的凸包(大概这意思吧。。。)。后来搜了一下,发现这种凸包叫做稳定凸包。
首先来了解什么是稳定的凸包。比如有4个点:
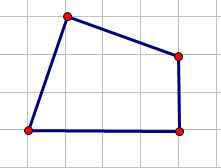 这四个点是某个凸包上的部分点,他们连起来后确实还是一个凸包。但是原始的凸包可能不是这样。比如:
这四个点是某个凸包上的部分点,他们连起来后确实还是一个凸包。但是原始的凸包可能不是这样。比如: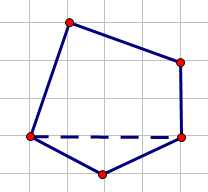
即这四个点构成的凸包不算做“稳定”的。我们发现,当凸包上存在一条边上的点只有端点两个点的时候,这个凸包不是稳定的,因为它可以在这条边外再引入一个点,构成一个新的凸包。但一旦一条边上存在三个点,那么不可能再找到一个点使它扩展成一个新的凸包,否则构成的新多边形将是凹的。
下面是一个典型的稳定凸包:
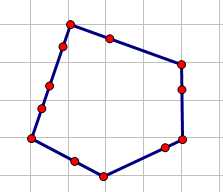
那么这道题的做法终于明确了。即求出给定这堆点的新的凸包,然后判断凸包上的每条边上是否至少有3个点存在,假如有一条边不符合条件,则输出NO。否则YES。
写的时候又遇到几个小问题了。。。一个是要修改一下凸包模板,大多数人的模板都是不包括共线点的。然后,如果输入的点数n小于6,那么直接输出NO。当然,也可以直接按极角排序进行比较。至于判断一条边上是否至少有三个点,我是这样做的,假设要判断的边i,那么判断边i和边i-1,边i和边i+1的夹角是否都为0(180)。
#include<iostream>
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<math.h>
#include<algorithm>
#include<queue>
#include<vector>
using namespace std;
const double eps=1e-9;
int cmp(double x)
{
if(fabs(x)<eps)return 0;
if(x>0)return 1;
else return -1;
}
const double pi=acos(-1.0);
inline double sqr(double x)
{
return x*x;
}
struct point
{
double x,y;
point (){}
point (double a,double b):x(a),y(b){}
void input()
{
scanf("%lf%lf",&x,&y);
}
friend point operator +(const point &a,const point &b)
{
return point(a.x+b.x,a.y+b.y);
}
friend point operator -(const point &a,const point &b)
{
return point(a.x-b.x,a.y-b.y);
}
friend bool operator ==(const point &a,const point &b)
{
return cmp(a.x-b.x)==0&&cmp(a.y-b.y)==0;
}
friend point operator *(const point &a,const double &b)
{
return point(a.x*b,a.y*b);
}
friend point operator*(const double &a,const point &b)
{
return point(a*b.x,a*b.y);
}
friend point operator /(const point &a,const double &b)
{
return point(a.x/b,a.y/b);
}
double norm()
{
return sqrt(sqr(x)+sqr(y));
}
};
struct line
{
point a,b;
line(){};
line(point x,point y):a(x),b(y)
{
}
};
double det(const point &a,const point &b)
{
return a.x*b.y-a.y*b.x;
}
double dot(const point &a,const point &b)
{
return a.x*b.x+a.y*b.y;
}
double dist(const point &a,const point &b)
{
return (a-b).norm();
}
point rotate_point(const point &p,double A)
{
double tx=p.x,ty=p.y;
return point(tx*cos(A)-ty*sin(A),tx*sin(A)+ty*cos(A));
}
bool parallel(line a,line b)
{
return !cmp(det(a.a-a.b,b.a-b.b));
}
bool line_joined(line a,line b,point &res)
{
if(parallel(a,b))return false;
double s1=det(a.a-b.a,b.b-b.a);
double s2=det(a.b-b.a,b.b-b.a);
res=(s1*a.b-s2*a.a)/(s1-s2);
return true;
}
bool pointonSegment(point p,point s,point t)
{
return cmp(det(p-s,t-s))==0&&cmp(dot(p-s,p-t))<=0;
}
void PointProjLine(const point p,const point s,const point t,point &cp)
{
double r=dot((t-s),(p-s))/dot(t-s,t-s);
cp=s+r*(t-s);
}
struct polygon_convex
{
vector<point>P;
polygon_convex(int Size=0)
{
P.resize(Size);
}
};
bool comp_less(const point &a,const point &b)
{
return cmp(a.x-b.x)<0||cmp(a.x-b.x)==0&&cmp(a.y-b.y)<0;
}
polygon_convex convex_hull(vector<point> a)
{
polygon_convex res(2*a.size()+5);
sort(a.begin(),a.end(),comp_less);
a.erase(unique(a.begin(),a.end()),a.end());//删去重复点
int m=0;
//cout<<a.size()<<endl;
for(int i=0;i<a.size();i++)
{
while(m>1&&cmp(det(res.P[m-1]-res.P[m-2],a[i]-res.P[m-2]))<0)--m;
res.P[m++]=a[i];
}
int k=m;
for(int i=int(a.size())-2;i>=0;--i)
{
while(m>k&&cmp(det(res.P[m-1]-res.P[m-2],a[i]-res.P[m-2]))<0)--m;
res.P[m++]=a[i];
}
res.P.resize(m);
if(a.size()>1)res.P.resize(m-1);
return res;
}
bool is_convex(vector<point> &a)
{
for(int i=0;i<a.size();i++)
{
int i1=(i+1)%int(a.size());
int i2=(i+2)%int(a.size());
int i3=(i+3)%int(a.size());
if((cmp(det(a[i1]-a[i],a[i2]-a[i1]))*cmp(det(a[i2]-a[i1],a[i3]-a[i2])))<0)
return false;
}
return true;
}
int containO(const polygon_convex &a,const point &b)
{
int n=a.P.size();
point g=(a.P[0]+a.P[n/3]+a.P[2*n/3])/3.0;
int l=0,r=n;
while(l+1<r)
{
int mid=(l+r)/2;
if(cmp(det(a.P[l]-g,a.P[mid]-g))>0)
{
if(cmp(det(a.P[l]-g,b-g))>=0&&cmp(det(a.P[mid]-g,b-g))<0)r=mid;
else l=mid;
}else
{
if(cmp(det(a.P[l]-g,b-g))<0&&cmp(det(a.P[mid]-g,b-g))>=0)l=mid;
else r=mid;
}
}
r%=n;
int z=cmp(det(a.P[r]-b,a.P[l]-b))-1;
if(z==-2)return 1;
return z;
}
bool circle_in_polygon(point cp,double r,polygon_convex &pol)
{
polygon_convex pp=convex_hull(pol.P);
if(containO(pp,cp)!=1)return false;
for(int i=0;i<pol.P.size();i++)
{
int j;
if(i<pol.P.size()-1)j=i+1;
else j=0;
point prol;
PointProjLine(cp,pol.P[i],pol.P[j],prol);
double dis;
if(pointonSegment(prol,pol.P[i],pol.P[j]))dis=dist(prol,cp);
else dis=min(dist(cp,pol.P[i]),dist(pol.P[j],cp));
if(cmp(dis-r)==-1)return false;
}
return true;
}
const int maxn=1e+6;
point po[maxn+10];
double area(point a[],int n)
{
double sum=0;
a[n]=a[0];
for(int i=0;i<n;i++)
sum+=det(a[i+1],a[i]);
return sum/2.;
}
int Point_in(point a[],int n,point t)
{
int num=0,i,d1,d2,k;
a[n]=a[0];
for(int i=0;i<n;i++)
{
if(pointonSegment(t,a[i],a[i+1]))return 2;
k=cmp(det(a[i+1]-a[i],t-a[i]));
d1=cmp(a[i].y-t.y);
d2=cmp(a[i+1].y-t.y);
if(k>0&&d1<=0&&d2>0)num++;
if(k<0&&d2<=0&&d1>0)num--;
}
return num!=0;
}
point pp[100];
int GCD(int a,int b)//Euclid
{
return b==0?a:GCD(b,a%b);
}
int Border_point_num(point a[],int n)
{
int num=0;
a[n]=a[0];
for(int i=0;i<n;i++)
num+=GCD(abs(int(a[i+1].x-a[i].x)),abs(int(a[i+1].y-a[i].y)));
return num;
}
int Inside_point_num(point a[],int n)
{
return int(-area(a,n))+1-Border_point_num(a,n)/2;
}
vector<point> p;
int main()
{freopen("t.txt","r",stdin);
int T;
scanf("%d",&T);
while(T--)
{
p.clear();
int n;
scanf("%d",&n);
p.resize(n);
for(int i=0;i<n;i++)
p[i].input();
if(n<6){printf("NO\n");continue;}
polygon_convex pc=convex_hull(p);
int i=0;
bool flag=true;
pc.P.push_back(pc.P[0]);
while(i<pc.P.size()-1&&flag)
{
flag=false;
if(i+2>=pc.P.size())break;
point p1=pc.P[i],p2=pc.P[i+1],p3=pc.P[i+2];
if(cmp(det(p2-p1,p3-p2))==0)flag=true;
else break;
i=i+3;
while((cmp(det(p2-p1,pc.P[i]-p2))==0)&&i<pc.P.size())i++;
i--;
}
if(flag)printf("YES\n");
else printf("NO\n");
}
return 0;
}
标签:cpp less tar [] put parallel 意思 const jline
原文地址:http://www.cnblogs.com/heisenberg-/p/6690645.html