标签:log 条件 删除 algorithm include cot const namespace .com
传送门:http://poj.org/problem?id=3258

题意:
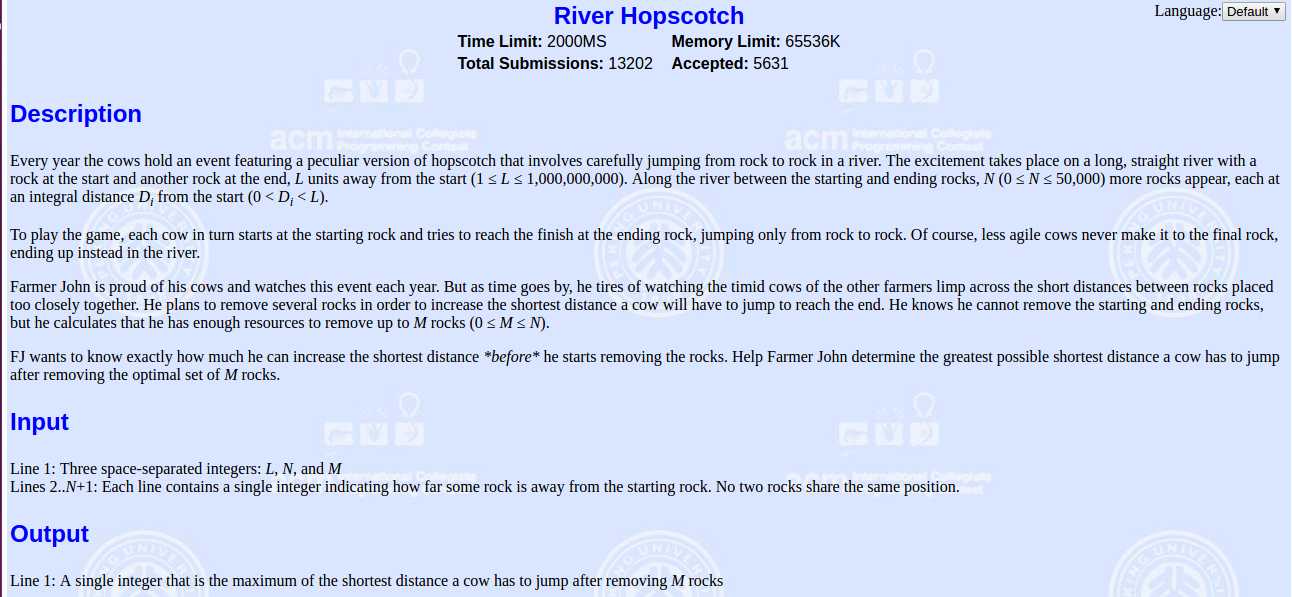
在一条河上有个起始点0,有个终点L,在终点和起始点间有N石头。每个石头距离起点的距离d (0<d<L)
例如0 2 11 14 17 21 25
除了终点和起点你可以删除2个,使得相邻两个石头的距离最小为多少。
解题思路:
设C(d):移除掉M个石头相邻连个石头见的距离为d。 0<=d<=L;
然后通过二分判断距离为d时是否满足条件,d是否能更大,
类似最大化最小值。
实现代码:
#include <iostream> #include <cstdio> #include <cstring> #include <algorithm> using namespace std; /* 这是一个求最下值最大化的问题: C(d):表示去掉M个牛,使得牛能到最短距离为d d的取值范围为:1<d<L 这样我们用二分枚举可能的值:d 若两个石头的距离小于d,然后就去除后面一个石头,最后在看去掉的石头数是否小于等于M */ const int MAXN=50005; int dist[MAXN]; int N,M,L;
//判断距离为mid是否满足题意 bool cal(int mid){ int last=0; int cnt=0; int crt=1; while(crt<=N){ if(dist[crt]-dist[last]<mid){ cnt++; crt+=1; }else{ last=crt; crt++; } } if(last!=0&&dist[crt]-dist[last]<mid) cnt++; if(cnt<=M) / return true; else return false; } int main(){ cin>>L>>N>>M; for(int i=1;i<=N;i++) scanf("%d",&dist[i]); dist[0]=0; dist[N+1]=L; sort(dist,dist+N+1); int l=0,r=L; int mid=0; if(N==M){ cout<<L<<endl; return 0; } while(r-l>1){ mid= (l+r)/2; if(cal(mid)){ l=mid; }else{ r=mid; } } cout<<l<<endl; return 0; }
标签:log 条件 删除 algorithm include cot const namespace .com
原文地址:http://www.cnblogs.com/IKnowYou0/p/6690887.html