机器学习（四） 概率论

标签：概率   而不是   最大化   错误   定义   优势   http   参数   nbsp   

概率论

举例说明

先验概率：一个病人 得了癌症的概率 

后验概率：一个病人 拍了片子，显示某个部位不正常时，得癌症的概率

似然函数 ： 一个病人，得了癌症，拍片子显示不正常的概率

标准化常量：拍片子不正常的概率

贝叶斯公式

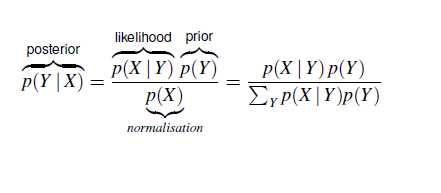
曲线拟合：

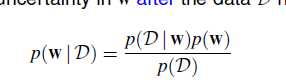
期中D表示 观测到的数据。

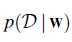
表示 在不同的w值下，这样的数据出现的可能性，而不是数据在参数w的情况下的概率密度

频率派估计：最大似然函数

求出一个w值，使得似然函数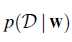

最大。即 求一个w值，使得被观测到的数据值的可能性最大。

机器学习：误差方程（error function）是 最大似然函数的负log

取对数是单调函数（monoton）

最大化似然等价于最小化误差

贝叶斯方法：

凭经验获得参数w

如果先验概率选择的很差，结果也会很差。

先验概率选择非常主观。

有时候甚至是为了数学计算上的简便而选择一些先验概率

需要对整个参数空间积分

在样本上有优势 MCMC算法

在近似的模式上有优势  Variation Bayes， Expectation Propagation.

决策论：

最小化误分率：找到边界x，使得x1∈R2，x2∈R1的概率最小。

最小化损失期望：对每个错误赋权，如 x1∈R2权1，x2∈R1权1000（ 如癌症检测中，误诊为癌症的损失要比有癌症而没有诊断出来要严重得多）

拒绝域： 如果后验概率明显小于1，则拒绝作出选项，进行进一步的判断。

S-fold 检验

将数据分为S组，用s-1组训练，剩下的一组用来测试。选择不同的训练与测试数据，进行s次。

机器学习（四） 概率论

标签：概率   而不是   最大化   错误   定义   优势   http   参数   nbsp   

原文地址：http://www.cnblogs.com/ChouPyroblast/p/6690856.html