标签:方向 images ima 向量 bsp graphics 平移 arc 公式
在图形学中,计算光照模型时,经常需要求取反射向量,一般的shader函数库都提供计算反射向量的方法,下面介绍一下如何手动计算反射向量。
给定入射光线向量I和平面法向量N,求反射向量R,如下图。为了方便计算,这里假定I和N都是单位向量(模为1,编程时可先将I和N单位化)
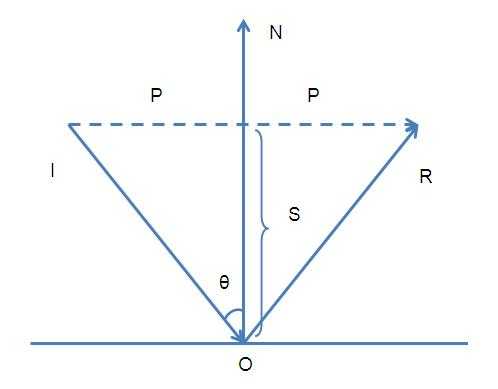
设入射光线向量I和反射平面的法向量N之间的夹角为theta。连接I的始端和R的末端,则有
R = 2P - I (1)
现在问题变成了如何求取P,设入射点0到P与N的交点的向量为S,那么有
P = I + S (2)
现在问题变成了如何求取向量S,向量S即向量-N(注意,这里是-N,因为S和N的方向相反。)在向量N上的投影,根据向量的投影公式有
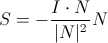
因为N是单位向量,简化一下得到
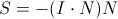
将S代入公式(2),再将P代入公式(1)得到
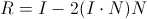
将R平移一下,与向量N的延长线相交。
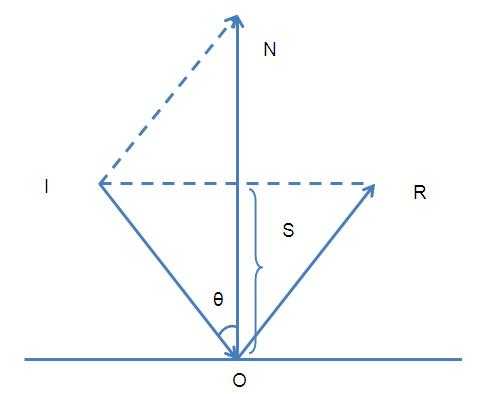
由于入射角和反射角相等,且I和R的长度也相等,所以三角形ION是等腰三角形。故有
ON = 2S
所以有
R = I + 2S
而S是-I在N上的投影,所以有
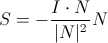
由于N是单位向量,简化一下得到
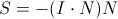
所以
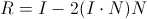
貌似方法二更直观些。
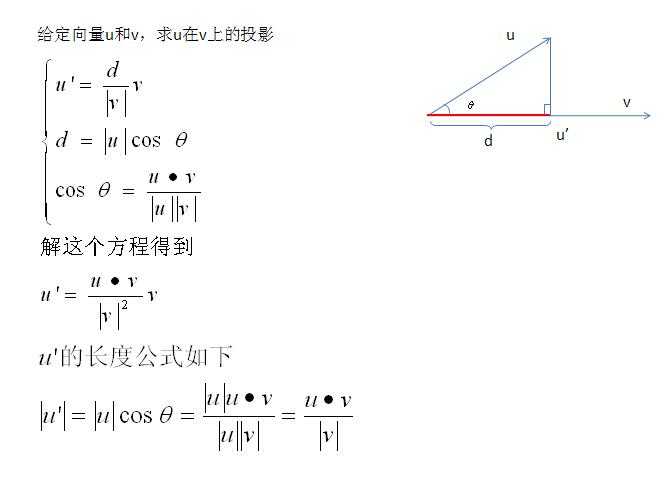
给定一个向量u和v,求u在v上的投影向量,如下图。
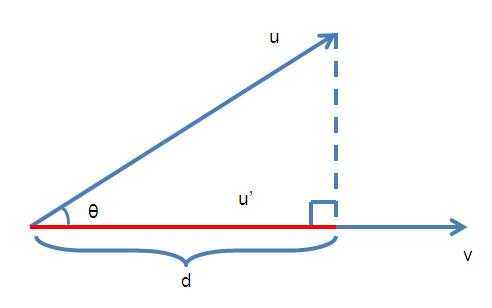
假设u在v上的投影向量是u’,且向量u和v的夹角为theta。一个向量有两个属性,大小和方向,我们先确定u’的大小(即长度,或者模),从u的末端做v的垂线,那么d就是u’的长度。而u’和v的方向是相同的,v的方向v/|v|也就是u’的方向。所以有
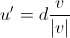 (1)
(1)
再求d的长度。
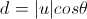 (2)
(2)
最后求cos(theta)
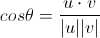 (3)
(3)
联合求解方程(1)(2)(3)得到
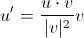
这就是最终的投影向量。
而这个向量的长度d是
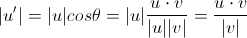
============================
以下是旧的推导,也保留。
标签:方向 images ima 向量 bsp graphics 平移 arc 公式
原文地址:http://www.cnblogs.com/mazhenyu/p/6700268.html