标签:style blog http color os io for ar 2014
【题意】:
给出N,M,代表N个学科,然后给出N个数,第i个数代表第i门课程可以学到的最大进度,初始时一个人所有课程学习进度都为0
然后M行 每行有5个数 c,L1,d,L2,cost代表一次培训
该培训需要c课程的学习进度为L1,然后使d课程的学习进度增长至L2,花费cost,问使所有课程都学到最大进度所需要的最小花费
【知识点】:
最小树形图
【题解】:
首先再次为自己科普下最小树形图的知识
最小树形图,就是给有向带权图中指定一个特殊的点root,求一棵以root为根的有向生成树T,并且T中所有边的总权值最小。
建图也是这道题的亮点
比如说样例
3 4
3 3 1
1 0 2 3 10
2 1 1 2 10
1 2 3 1 10
3 1 1 3 10
0 0
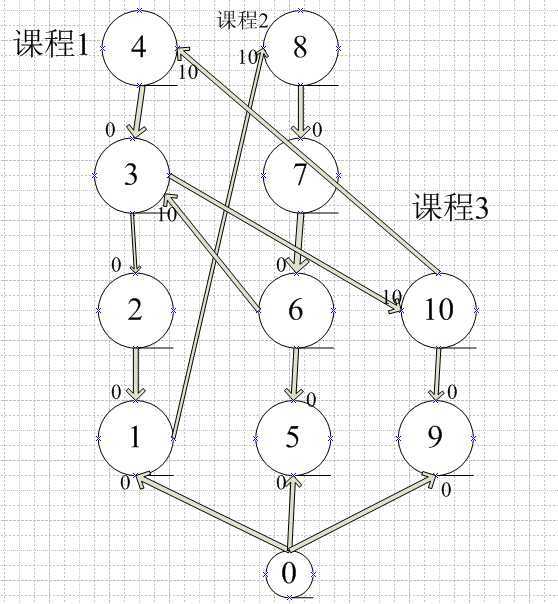
建图应该这样
0点连每门课学习进度为0对应的点,然后每门课学习进度为i的点连接该门课学习进度为i-1的点(因为学到该进度必然学到比该进度小的进度),费用为0。
培训中某门课需要的进度对应的点连接可将另外一门课培训至某进度对应的点,费用为给出的费用。
我对最小树形图的算法还不甚了解,以后学到更深处时会继续更新该篇文章的。
【代码】:

1 #include <map> 2 #include <set> 3 #include <cmath> 4 #include <ctime> 5 #include <queue> 6 #include <stack> 7 #include <cstdio> 8 #include <string> 9 #include <vector> 10 #include <cstring> 11 #include <sstream> 12 #include <iostream> 13 #include <algorithm> 14 #include <bitset> 15 #include <climits> 16 using namespace std; 17 18 #define wh while 19 #define inf (int)(~0u/2) 20 #define FOR(i, n) for(int i = 0; i < n; i++) 21 #define FOR1(i, n) for(int i = 1; i < n; i++) 22 #define FOR2(i, n) for(int i = 0; i <= n; i++) 23 #define REP(i,n) for(int i = 1; i <= n; i++) 24 #define FORI(it,n) for(typeof(n.begin()) it = n.begin(); it != n.end(); it++) 25 #define sf scanf 26 #define pf printf 27 #define frs first 28 #define sec second 29 #define psh push_back 30 #define mkp make_pair 31 #define PB(x) push_back(x) 32 #define MP(x, y) make_pair(x, y) 33 #define clr(abc,z) memset(abc,z,sizeof(abc)) 34 #define lt(v) v << 1 35 #define rt(v) v << 1 | 1 36 //#define mid ((l + r) >> 1) 37 //#define lson l, mid, v << 1 38 //#define rson mid + 1, r, v << 1 | 1 39 40 #define fre freopen("1.txt", "r", stdin) 41 #define freout freopen("1.txt", "w", stdout) 42 43 typedef long long LL; 44 typedef long double LD; 45 const int maxn = 600 + 5; 46 const int INF = 1e9; 47 // 固定根的最小树型图,邻接矩阵写法,时间复杂度O(n^3) 48 struct MDST { 49 int n; 50 int w[maxn][maxn]; // 边权 51 int vis[maxn]; // 访问标记,仅用来判断无解 52 int ans; // 计算答案 53 int removed[maxn]; // 每个点是否被删除 54 int cid[maxn]; // 所在圈编号 55 int pre[maxn]; // 最小入边的起点 56 int iw[maxn]; // 最小入边的权值 57 int max_cid; // 最大圈编号 58 59 void init(int n) { 60 this->n = n; 61 for(int i = 0; i < n; i++) 62 for(int j = 0; j < n; j++) w[i][j] = INF; 63 } 64 65 void AddEdge(int u, int v, int cost) { 66 w[u][v] = min(w[u][v], cost); 67 } 68 69 int dfs(int s) { 70 vis[s] = 1; int ans = 1; 71 for(int i = 0; i < n; i++) 72 if(!vis[i] && w[s][i] < INF) ans += dfs(i); 73 return ans; 74 } 75 bool cycle(int u) { 76 max_cid++; int v = u; 77 while(cid[v] != max_cid) { 78 cid[v] = max_cid; v = pre[v]; 79 } 80 return v == u; 81 } 82 void update(int u) { 83 iw[u] = INF; 84 for(int i = 0; i < n; i++) 85 if(!removed[i] && w[i][u] < iw[u]) { 86 iw[u] = w[i][u]; pre[u] = i; 87 } 88 } 89 bool solve(int s) { 90 memset(vis, 0, sizeof(vis)); 91 if(dfs(s) != n) return false; 92 memset(removed, 0, sizeof(removed)); 93 memset(cid, 0, sizeof(cid)); 94 for(int u = 0; u < n; u++) update(u); 95 pre[s] = s; iw[s] = 0; 96 ans = max_cid = 0; 97 for(;;) { 98 bool have_cycle = false; 99 for(int u = 0; u < n; u++) if(u != s && !removed[u] && cycle(u)) { 100 have_cycle = true; 101 int v = u; 102 do { 103 if(v != u) removed[v] = 1; 104 ans += iw[v]; 105 for(int i = 0; i < n; i++) if(cid[i] != cid[u] && !removed[i]) { 106 if(w[i][v] < INF) w[i][u] = min(w[i][u], w[i][v]-iw[v]); 107 w[u][i] = min(w[u][i], w[v][i]); 108 if(pre[i] == v) pre[i] = u; 109 } 110 v = pre[v]; 111 } while(v != u); 112 update(u); break; 113 } 114 if(!have_cycle) break; 115 } 116 for(int i = 0; i < n; i++) 117 if(!removed[i]) ans += iw[i]; 118 return true; 119 } 120 } solver; 121 int a[maxn], id[maxn]; 122 123 int main(){ 124 int N, M; 125 wh(sf("%d%d", &N, &M) != EOF){ 126 if(!N && !M) break; 127 id[1] = 0; int all = 0; 128 REP(i, N){ 129 sf("%d", &a[i]); 130 id[i + 1] = id[i] + a[i] + 1; 131 all += (a[i] + 1); 132 } 133 solver.init(all + 1); 134 REP(i, N){ 135 solver.AddEdge(0, id[i] + 1, 0); 136 REP(j, a[i]) 137 solver.AddEdge(id[i] + j + 1, id[i] + j, 0); 138 } 139 FOR(i, M){ 140 int c, l1, d, l2, cost; sf("%d%d%d%d%d", &c, &l1, &d, &l2, &cost); 141 solver.AddEdge(id[c] + l1 + 1, id[d] + l2 + 1, cost); 142 } 143 if(solver.solve(0)) 144 pf("%d\n", solver.ans); 145 else 146 pf("-1\n"); 147 } 148 }
标签:style blog http color os io for ar 2014
原文地址:http://www.cnblogs.com/Ntcrush/p/3932806.html