标签:单调队列 技术 技术分享 队列 [] ini include 操作 长度
给你一个长度为N的数组,一个长为K的滑动的窗体从最左移至最右端,你只能见到窗口的K个数,每次窗体向右移动一位,如下表: 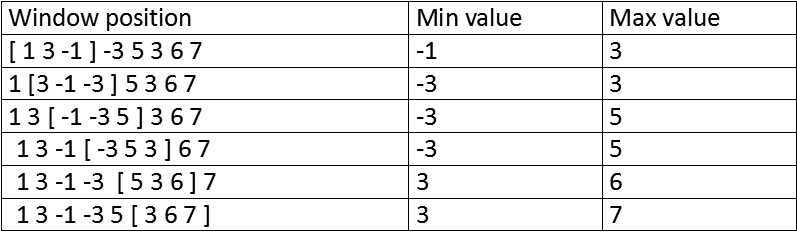
你的任务是找出窗口在各位置时的max value,min value.
单调队列的入门题,单调队列我的理解有对时间和大小都单调,只会在队列两端进行操作(队尾前移看大小,队头后移看时间),不会有元素插入到之前的两元素之间,因此每次都能保证队头元素是符合要求的
1 //O(n) 2 #include<bits/stdc++.h> 3 using namespace std; 4 const int N = 1000 + 5; 5 int a[N]; 6 7 struct MonotonicQueue { 8 int minv[N], maxv[N], q[N], id[N], n, k; 9 10 void init(int n, int k) { 11 this->n = n; this->k = k; 12 } 13 14 void getmax(int a[]) { 15 int head = 0, tail = 0; 16 for (int i = 0; i < k-1; ++i) { 17 while (head < tail && q[tail-1] <= a[i]) --tail; 18 id[tail] = i; 19 q[tail++] = a[i]; 20 } 21 for (int i = k-1; i < n; ++i) { 22 while (head < tail && q[tail-1] <= a[i]) --tail; 23 id[tail] = i; 24 q[tail++] = a[i]; 25 while (id[head] < i-k+1) ++head; 26 for (int j = head; j < tail; ++j) cout << q[j] << " "; 27 cout << endl; 28 maxv[i-k+1] = q[head]; 29 } 30 } 31 32 void getmin(int a[]) { 33 int head = 0, tail = 0; 34 for (int i = 0; i < k-1; ++i) { 35 while (head < tail && q[tail-1] >= a[i]) --tail; 36 id[tail] = i; 37 q[tail++] = a[i]; 38 } 39 for (int i = k-1; i < n; ++i) { 40 while (head < tail && q[tail-1] >= a[i]) --tail; 41 id[tail] = i; 42 q[tail++] = a[i]; 43 while (id[head] < i-k+1) ++head; 44 minv[i-k+1] = q[head]; 45 } 46 } 47 48 }mq; 49 50 int main() { 51 int n, k; 52 while (~scanf("%d%d", &n, &k)) { 53 mq.init(n, k); 54 for (int i = 0; i < n; ++i) scanf("%d", &a[i]); 55 mq.getmax(a); mq.getmin(a); 56 for (int i = 0; i < n-k+1; ++i) 57 printf("%d %d\n", mq.minv[i], mq.maxv[i]); 58 } 59 60 return 0; 61 }
标签:单调队列 技术 技术分享 队列 [] ini include 操作 长度
原文地址:http://www.cnblogs.com/robin1998/p/6715404.html