标签:because ldo ccf sha smi array gets abc 9.png
| 语法 | 效果 | 语法 | 效果 | 语法 | 效果 |
|---|---|---|---|---|---|
| \bar{x} | 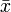 |
\acute{\eta} |  |
\check{\alpha} | 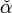 |
| \grave{\eta} |  |
\breve{a} |  |
\ddot{y} |  |
| \dot{x} |  |
\hat{\alpha} |  |
\tilde{\iota} |  |
| 语法 | 效果 | 语法 | 效果 | 语法 | 效果 |
|---|---|---|---|---|---|
| \sin\theta | 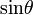 |
\cos\theta |  |
\tan\theta | 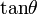 |
| \arcsin\frac{L}{r} |  |
\arccos\frac{T}{r} |  |
\arctan\frac{L}{T} |  |
| \sinh g |  |
\cosh h |  |
\tanh i |  |
| \operatorname{sh}j | 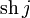 |
\operatorname{argsh}k |  |
\operatorname{ch}h | 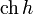 |
| \operatorname{argch}l |  |
\operatorname{th}i | 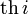 |
\operatorname{argth}m |  |
| k‘(x)=\lim_{\Delta x\to 0}\frac{k(x)-k(x-\Delta x)}{\Deltax} | 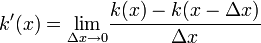 |
\limsup S |  |
\liminf I | 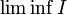 |
| \max H | 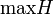 |
\min L | 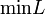 |
\inf s |  |
| \sup t | 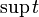 |
\exp\!t |  |
\ln X | 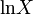 |
| \lg X |  |
\log X | 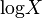 |
\log_\alpha X |  |
| \ker x | 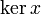 |
\deg x |  |
\gcd(T,U,V,W,X) |  |
| \Pr x |  |
\det x | 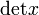 |
\hom x |  |
| \arg x |  |
\dim x | 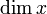 |
\lim_{t\to n}T |  |
| 语法 | 效果 | 语法 | 效果 |
|---|---|---|---|
| \pmod{m} |  |
a \bmod b |  |
| 语法 | 效果 | 语法 | 效果 | 语法 | 效果 |
|---|---|---|---|---|---|
| \nabla |  |
\partial x |  |
\mathrm{d}x | 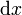 |
| \dot x | 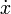 |
\ddot y |  |
| 语法 | 效果 | 语法 | 效果 | 语法 | 效果 | 语法 | 效果 | 语法 | 效果 |
|---|---|---|---|---|---|---|---|---|---|
| \forall | 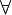 |
\exists | 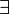 |
\empty | 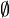 |
\emptyset | 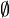 |
\varnothing | 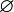 |
| \in |  |
\ni |  |
\not\in |  |
\notin | 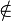 |
\subset |  |
| \subseteq |  |
\supset | 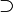 |
\supseteq |  |
\cap | 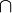 |
\bigcap |  |
| \cup |  |
\bigcup |  |
\biguplus | 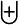 |
\sqsubset |  |
\sqsubseteq |  |
| \sqsupset |  |
\sqsupseteq | 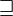 |
\sqcap |  |
\sqcup |  |
\bigsqcup |  |
| 语法 | 效果 | 语法 | 效果 | 语法 | 效果 | 语法 | 效果 |
|---|---|---|---|---|---|---|---|
| p |  |
\land | 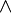 |
\wedge | 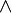 |
\bigwedge |  |
| \bar{q} \to p |  |
\lor |  |
\vee | 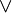 |
\bigvee | 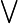 |
| \lnot |  |
\neg q |  |
\setminus |  |
\smallsetminus | 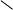 |
| 语法 | 效果 | 语法 | 效果 |
|---|---|---|---|
| \sqrt{3} |  |
\sqrt[n]{3} |  |
| 语法 | 效果 |
|---|---|
\Delta ABC\sim\Delta XYZ |
 |
\sqrt{3}\approx1.732050808\ldots |
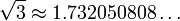 |
| \simeq | 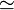 |
| \cong |  |
| \dot= |  |
\ggg |
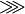 |
\gg |
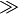 |
> |
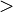 |
\ge |
 |
\geqq |
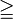 |
= |
 |
\leq |
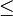 |
\leqq |
 |
< |
 |
\ll |
 |
\lll |
 |
(x-y)^2\equiv(-x+y)^2\equiv x^2-2xy+y^2 |
 |
|
|
 |
| x\not\equiv N | 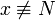 |
| x\ne A |  |
| x\neq C | 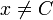 |
| t\propto v |  |
| \pm | 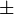 |
| \mp | 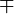 |
| 特征 | 语法 | 效果 | |
|---|---|---|---|
| 菱形 | \Diamond | 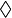 |
|
| 正方形 | \Box |  |
|
| 三角形 | Delta | \Delta |
 |
| 图型 | \triangle |
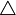 |
|
| 角名 | \angle\Alpha\Beta\Gamma |
 |
|
| 角度 | \sin\!\frac{\pi}{3}=\sin60^\operatorname{\omicron}=\frac{\sqrt{3}}{2} |
 |
|
| 垂直 | \perp | 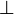 |
|
| 语法 | 效果 | 语法 | 效果 | 语法 | 效果 |
|---|---|---|---|---|---|
| \leftarrow |  |
\gets | 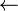 |
\rightarrow | 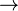 |
| \to |  |
\leftrightarrow |  |
\longleftarrow |  |
| \longrightarrow |  |
\mapsto |  |
\longmapsto | 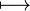 |
| \hookrightarrow |  |
\hookleftarrow | 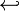 |
\nearrow |  |
| \searrow |  |
\swarrow |  |
\nwarrow |  |
| \uparrow | 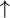 |
\downarrow | 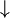 |
\updownarrow | 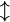 |
| 语法 | 效果 | 语法 | 效果 | 语法 | 效果 | 语法 | 效果 |
|---|---|---|---|---|---|---|---|
| \rightharpoonup |  |
\rightharpoondown |  |
\leftharpoonup |  |
\leftharpoondown |  |
| \upharpoonleft | 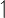 |
\upharpoonright |  |
\downharpoonleft |  |
\downharpoonright |  |
| 语法 | 效果 | 语法 | 效果 | 语法 | 效果 |
|---|---|---|---|---|---|
| \Leftarrow | 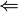 |
\Rightarrow | 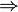 |
\Leftrightarrow | 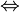 |
| \Longleftarrow |  |
\Longrightarrow |  |
\Longleftrightarrow (or \iff) | 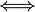 |
| \Uparrow |  |
\Downarrow |  |
\Updownarrow |  |
| 语法 | 效果 | 语法 | 效果 | 语法 | 效果 | 语法 | 效果 | 语法 | 效果 | 语法 | 效果 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| \eth |  |
\S | 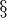 |
\P |  |
\% |  |
\dagger | 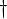 |
\ddagger | 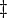 |
| \star |  |
* | 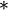 |
\ldots | 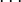 |
\smile |  |
\frown | 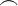 |
\wr | 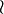 |
| 语法 | 效果 | 语法 | 效果 | 语法 | 效果 |
|---|---|---|---|---|---|
| \oplus |  |
\bigoplus |  |
\otimes | 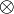 |
| \bigotimes |  |
\times |  |
\cdot |  |
| \div |  |
\circ |  |
\bullet |  |
| \bigodot |  |
\boxtimes |  |
\boxplus |  |
| 语法 | 效果 | 语法 | 效果 | 语法 | 效果 | 语法 | 效果 |
|---|---|---|---|---|---|---|---|
| \triangleleft |  |
\triangleright |  |
\infty |  |
\bot |  |
| \top |  |
\vdash | 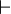 |
\vDash | 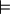 |
\Vdash |  |
| \models |  |
\lVert |  |
\rVert | 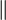 |
| 语法 | 效果 | 语法 | 效果 | 语法 | 效果 |
|---|---|---|---|---|---|
| \imath |  |
\hbar | 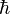 |
\ell | 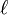 |
| \mho |  |
\Finv | 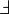 |
\Re | 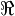 |
| \Im | 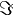 |
\wp | 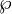 |
\complement |  |
| 语法 | 效果 | 语法 | 效果 | 语法 | 效果 | 语法 | 效果 |
|---|---|---|---|---|---|---|---|
| \diamondsuit | 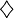 |
\heartsuit |  |
\clubsuit |  |
\spadesuit |  |
| \Game |  |
\flat |  |
\natural | 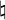 |
\sharp | 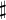 |
| 功能 | 语法 | 效果 |
|---|---|---|
| 上标 | a^2 |
 |
| 下标 | a_2 |
 |
| 组合 | a^{2+2} |
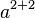 |
a_{i,j} |
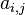 |
|
| 结合上下标 | x_2^3 |
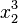 |
| 前置上下标 | {}_1^2\!X_3^4 |
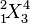 |
| 导数 (HTML) |
x‘ |
 |
| 导数 (PNG) |
x^\prime |
 |
| 导数 (错误) |
x\prime |
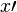 |
| 导数点 | \dot{x} |
 |
\ddot{y} |
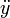 |
|
| 向量 | \vec{c} |
 |
\overleftarrow{a b} |
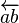 |
|
\overrightarrow{c d} |
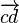 |
|
\widehat{e f g} |
 |
|
| 上弧 (注: 正确应该用 \overarc, 但在这里行不通。要用建议的语法作为解决办法) |
\overset{\frown} {AB} |
 |
| 上划线 | \overline{h i j} |
 |
| 下划线 | \underline{k l m} |
 |
| 上括号 | \overbrace{1+2+\cdots+100} |
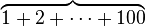 |
\begin{matrix} 5050 \\ \overbrace{ 1+2+\cdots+100 }\end{matrix} |
 |
|
| 下括号 | \underbrace{a+b+\cdots+z} |
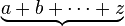 |
\begin{matrix} \underbrace{ a+b+\cdots+z } \\ 26\end{matrix} |
 |
|
| 求和 | \sum_{k=1}^N k^2 |
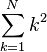 |
\begin{matrix} \sum_{k=1}^N k^2 \end{matrix} |
 |
|
| 求积 | \prod_{i=1}^N x_i |
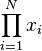 |
\begin{matrix} \prod_{i=1}^N x_i \end{matrix} |
 |
|
| 上积 | \coprod_{i=1}^N x_i |
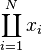 |
\begin{matrix} \coprod_{i=1}^N x_i\end{matrix} |
 |
|
| 极限 | \lim_{n \to \infty}x_n |
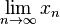 |
\begin{matrix} \lim_{n \to \infty}x_n\end{matrix} |
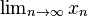 |
|
| 积分 | \int_{-N}^{N} e^x\, dx |
 |
\begin{matrix} \int_{-N}^{N} e^x\, dx\end{matrix} |
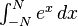 |
|
| 双重积分 | \iint_{D}^{W} \, dx\,dy |
 |
| 三重积分 | \iiint_{E}^{V} \, dx\,dy\,dz |
 |
| 四重积分 | \iiiint_{F}^{U} \, dx\,dy\,dz\,dt |
 |
| 闭合的曲线、曲面积分 | \oint_{C} x^3\, dx + 4y^2\, dy |  |
| 交集 | \bigcap_1^{n} p |
 |
| 并集 | \bigcup_1^{k} p |
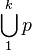 |
| 功能 | 语法 | 效果 |
|---|---|---|
| 分数 | \frac{2}{4}=0.5 |
 |
| 小型分数 | \tfrac{2}{4} = 0.5 |
 |
| 大型分数(嵌套) | \cfrac{2}{c + \cfrac{2}{d + \cfrac{2}{4}}} =a |
 |
| 大型分数(不嵌套) | \dfrac{2}{4} = 0.5 \qquad \dfrac{2}{c + \dfrac{2}{d +\dfrac{2}{4}}} = a |
 |
| 二项式系数 | \dbinom{n}{r}=\binom{n}{n-r}=C^n_r=C^n_{n-r} |
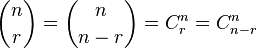 |
| 小型二项式系数 | \tbinom{n}{r}=\tbinom{n}{n-r}=C^n_r=C^n_{n-r} |
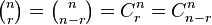 |
| 大型二项式系数 | \binom{n}{r}=\dbinom{n}{n-r}=C^n_r=C^n_{n-r} |
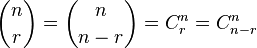 |
| 矩阵 |
\begin{matrix}
x & y \z & v
\end{matrix}
|
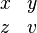 |
\begin{vmatrix}
x & y \z & v
\end{vmatrix}
|
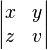 |
|
\begin{Vmatrix}
x & y \z & v
\end{Vmatrix}
|
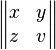 |
|
\begin{bmatrix}
0 & \cdots & 0 \\vdots & \ddots & \vdots \0 & \cdots & 0
\end{bmatrix}
|
 |
|
\begin{Bmatrix}
x & y \z & v
\end{Bmatrix}
|
 |
|
\begin{pmatrix}
x & y \z & v
\end{pmatrix}
|
 |
|
\bigl( \begin{smallmatrix}
a&b\\ c&d
\end{smallmatrix} \bigr)
|
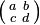 |
|
| 条件定义 |
f(n) =
\begin{cases}
n/2, & \mbox{if }n\mbox{ is even} \3n+1, & \mbox{if }n\mbox{ is odd}
\end{cases}
|
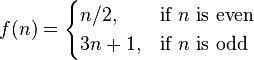 |
| 多行等式 |
\begin{align}
f(x) & = (m+n)^2 \& = m^2+2mn+n^2 \\end{align}
|
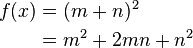 |
\begin{alignat}{2}
f(x) & = (m-n)^2 \f(x) & = (-m+n)^2 \& = m^2-2mn+n^2 \\end{alignat}
|
 |
|
| 多行等式(左对齐) |
\begin{array}{lcl}
z & = & a \f(x,y,z) & = & x + y + z
\end{array}
|
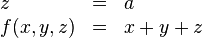 |
| 多行等式(右对齐) |
\begin{array}{lcr}
z & = & a \f(x,y,z) & = & x + y + z
\end{array}
|
 |
| 长公式换行 |
<math>f(x) \,\!</math>
<math>= \sum_{n=0}^\infty a_n x^n </math>
<math>= a_0+a_1x+a_2x^2+\cdots</math>
|
|
| 方程组 |
\begin{cases}
3x + 5y + z \7x - 2y + 4z \-6x + 3y + 2z
\end{cases}
|
 |
| 数组 |
\begin{array}{|c|c||c|} a & b & S \\hline
0&0&1\0&1&1\1&0&1\1&1&0\\end{array}
|
 |
斜体小写希腊字母一般用于在方程中显示变量。
| 特征 | 语法 | 效果 | 注释/外部链接 |
|---|---|---|---|
\Alpha \Beta \Gamma \Delta \Epsilon \Zeta \Eta\Theta |
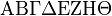 |
||
\Iota \Kappa \Lambda \Mu \Nu \Xi \Omicron \Pi |
 |
||
\Rho \Sigma \Tau \Upsilon \Phi \Chi \Psi\Omega |
 |
||
\alpha \beta \gamma \delta \epsilon \zeta \eta\theta |
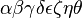 |
||
\iota \kappa\varkappa \lambda \mu \nu \xi \omicron\pi |
 |
||
\rho \sigma \tau \upsilon \phi \chi \psi\omega |
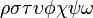 |
||
\Epsilon\epsilon\varepsilon |
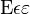 |
||
\Theta\theta\vartheta |
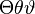 |
||
\Kappa\kappa\varkappa |
 |
||
\Pi\pi\varpi |
 |
||
\Rho\rho\varrho |
 |
||
\Sigma\sigma\varsigma |
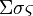 |
||
\Phi\phi\varphi |
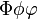 |
||
\digamma |
 |
||
| 特征 | 语法 | 效果 |
|---|---|---|
\boldsymbol{\Alpha \Beta \Gamma \Delta \Epsilon \Zeta\Eta \Theta} |
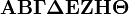 |
|
\boldsymbol{\Iota \Kappa \Lambda \Mu \Nu \Xi \Omicron\Pi} |
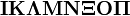 |
|
\boldsymbol{\Rho \Sigma \Tau \Upsilon \Phi \Chi \Psi\Omega} |
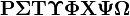 |
|
\boldsymbol{\alpha \beta \gamma \delta \epsilon \zeta\eta \theta} |
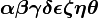 |
|
\boldsymbol{\iota \kappa \lambda \mu \nu \xi \omicron\pi} |
 |
|
\boldsymbol{\rho \sigma \tau \upsilon \phi \chi \psi\omega} |
 |
|
\boldsymbol{\Epsilon\epsilon\varepsilon} |
 |
|
\boldsymbol{\Theta\theta\vartheta} |
 |
|
\boldsymbol{\Kappa\kappa\varkappa} |
 |
|
\boldsymbol{\Pi\pi\varpi} |
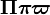 |
|
\boldsymbol{\Rho\rho\varrho} |
 |
|
\boldsymbol{\Sigma\sigma\varsigma} |
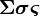 |
|
\boldsymbol{\Phi\phi\varphi} |
 |
|
标签:because ldo ccf sha smi array gets abc 9.png
原文地址:http://www.cnblogs.com/jiangxiaoxiu/p/6715509.html