标签:树的定义 删除 .com uri 算法思想 实现 this 方法 bin
代码的思想和图片参考:好大学慕课浙江大学陈越、何钦铭的《数据结构》
我们首先介绍一下什么是二叉搜索树和二叉平衡树:
二叉搜索树:一棵二叉树,可以为空;如果不为空,满足以下性质
1. 非空左子树的所有键值小于其根结点的键值。
2. 非空右子树的所有键值大于其根结点的键值。
3. 左、右子树都是二叉搜索树。
二叉搜索树操作的特别函数:
Position Find( ElementType X, BinTree BST ):从二叉搜索树BST
中查找元素X,返回其所在结点的地址,查找的次数取决于树的高度
算法思想:
和二分查找类似,如果大于根元素往右边找,小于根元素网左边找,可以使用递归和非递归的方法实现
注:对尾递归,可以用循环来实现。
Position FindMin( BinTree BST ):从二叉搜索树BST中查找并返回
最小元素所在结点的地址
算法思想:最小的元素在二叉搜索树的最左分支的端节点上。一直向左进行递归查找即可
Position FindMax( BinTree BST ) :从二叉搜索树BST中查找并返回
最大元素所在结点的地址
算法思想:最小的元素在二叉搜索树的最右分支的端节点上。一直向右进行递归查找即可
BinTree Insert( ElementType X, BinTree BST )
算法思想:和Find的方法差不多,先找到需要插入的位置,然后进行插入
BinTree Delete( ElementType X, BinTree BST )
算法思想:分为三种情况
1.删除的节点是叶子节点:直接删除
2.删除的节点只有一个孩子:删除该节点,把该节点的唯一的子节点挂到父节点上
3.该节点是有两个孩子的父节点:我们可以把两个孩子的节点看做是有一个孩子的父节点,但是必须从其子节点找到元素来
替换他,下面是找元素替换的方法。
3.1查找该节点左子树的最大元素,把最大元素的值给该节点,然后把那个左子树最大元素的节点删除
3.2查找该节点右子树的最小元素,把最小元素的值给该节点,然后把那个右子树最小元素的节点删除
为什么需要找最大或者最小元素呢,因为这样可以最大或者最小元素可以保证该节点只有一个子节点或者没有节点
否则找到一个具有两个节点的父节点,问题还是没有解决。
平衡二叉树:对于二叉搜索树来说,搜索的次数取决于树的高度,那么,由于元素的插入顺序和规则的不同
那么所生成树的形状和高度也不相同。可以参考讲义的十二个月份按照不同规则插入,造成二叉搜索树的高度差异有很大
我们希望树比较平衡,这样平均查找次数就比较少
定义:
平衡因子(Balance Factor,简称BF):BF(T)=hl-hr,
hl和hr为左右子树的高度
平衡二叉树的定义(Balance Binary tree 或者称为AVL树):
1.空树
2.任意节点左右子树的高度差不超过1,即|BF|<=1
那么我们需要思考,n个节点的平衡二叉树的高度为多少呢?能不能满足我们的需求呢。
我可以找规律,我们指定只有一个节点时,高度为0,那么就有如下规律
平衡二叉树的高度 平衡二叉树需要的最少节点个数
0 1 A
1 2
2 4
... ...
具体的规律和证明参考讲义,最终我们得到一个结论:给定节点为N的AVL树的最大高度为O(Log2 N)
平衡二叉树的调整问题:
为什么需要调整平衡儿茶树呢?因为我们队平衡二叉树的插入和删除操作,可能会破坏
树的平衡性,所以我们需要对树的平衡性进行调整。
注:数字代表平衡因子
注:数字代表平衡因子
调整的演示图
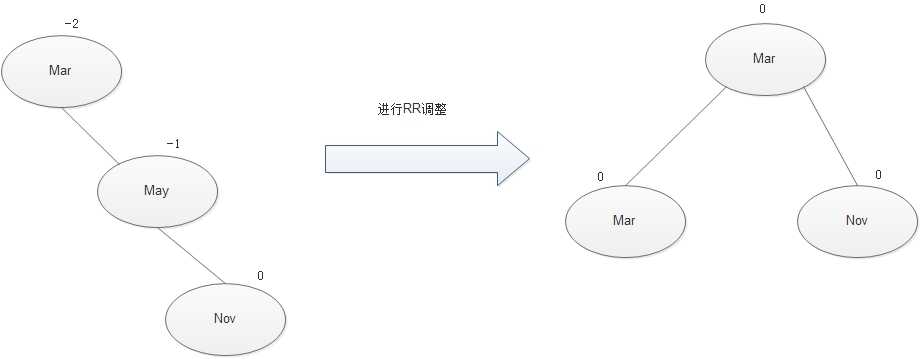
上面的不平衡的搜索树的发现者是Mar,麻烦节点是Nov,Nov在发现者的右子树的右边,因而叫做RR插入,需要进行RR旋转(右单旋)
下面给出RR调整的通用的图解:
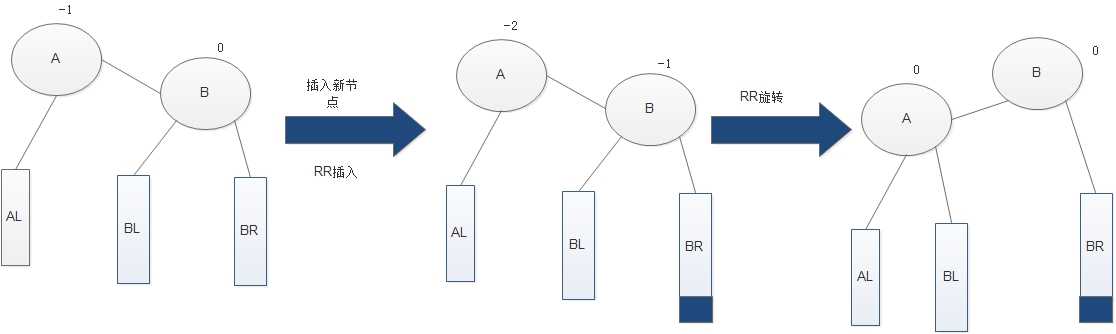
LL调整的演示图:
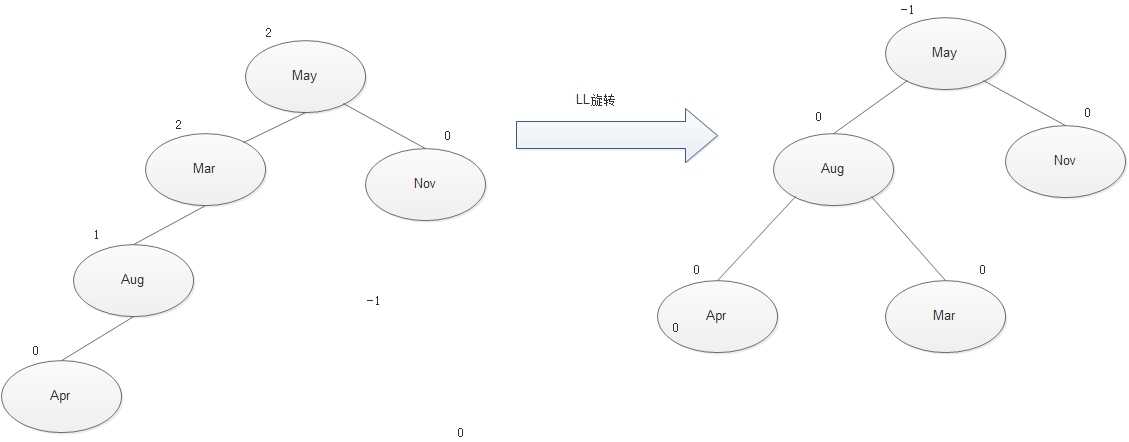
发现者Mar,麻烦节点为Apr在发现者的左子树的左边,因而叫LL插入,需要LL旋转
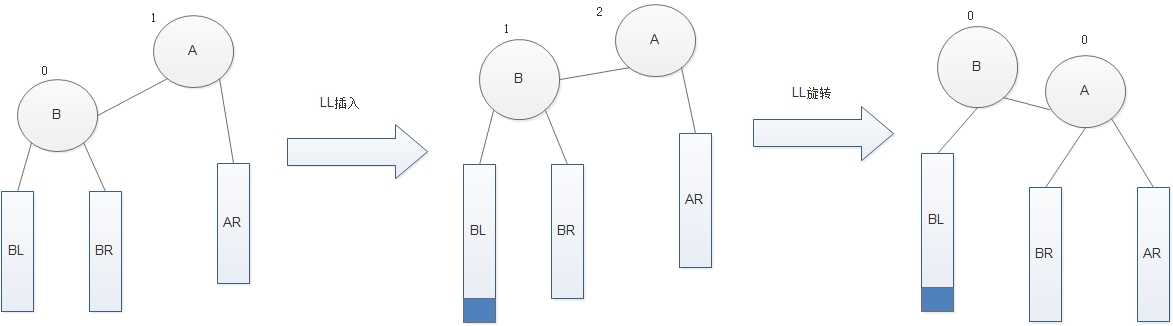
下面是LL调整的通解图:
LR调整的演示图
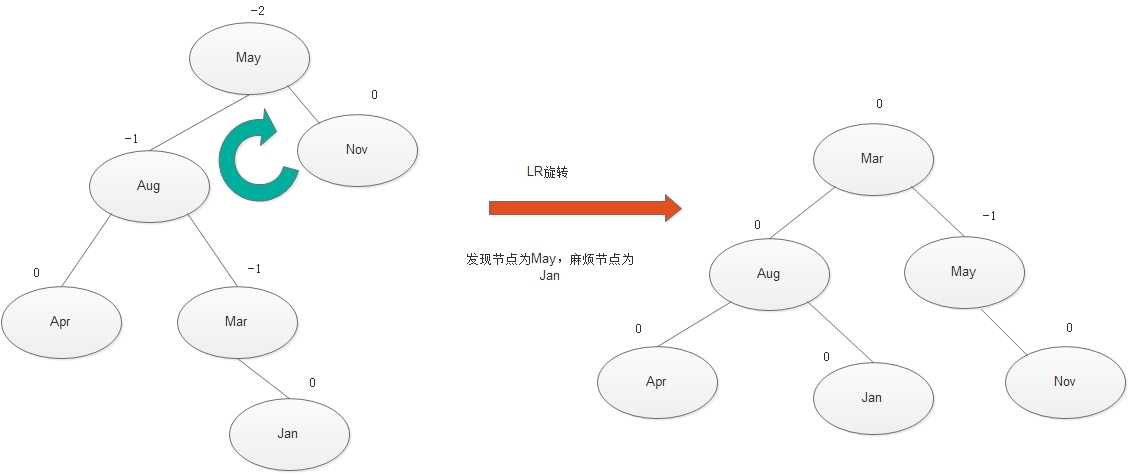
发现节点是May,麻烦节点是Jan,Jan在May左子树的右子树中,因而叫做LR插入,需要进行LR旋转
LR调整的通解图:
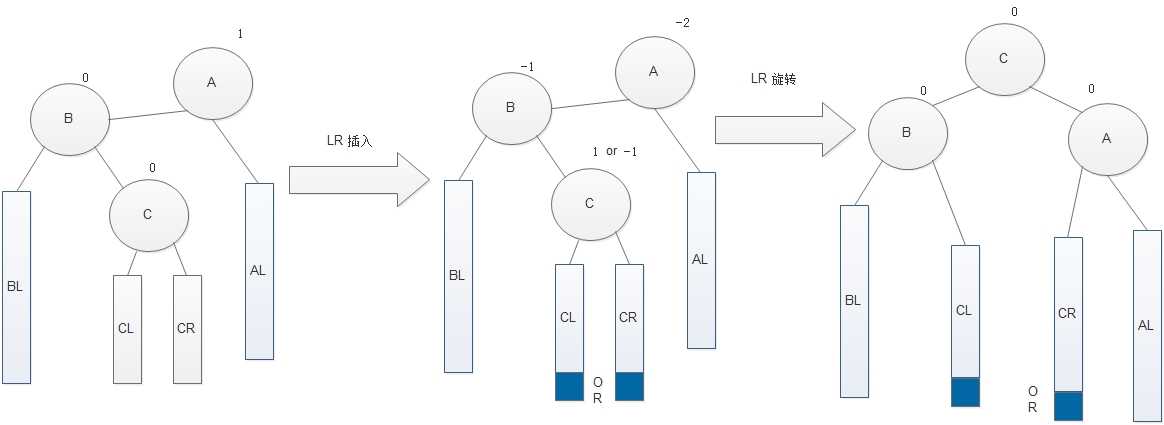
RL调整的演示图:
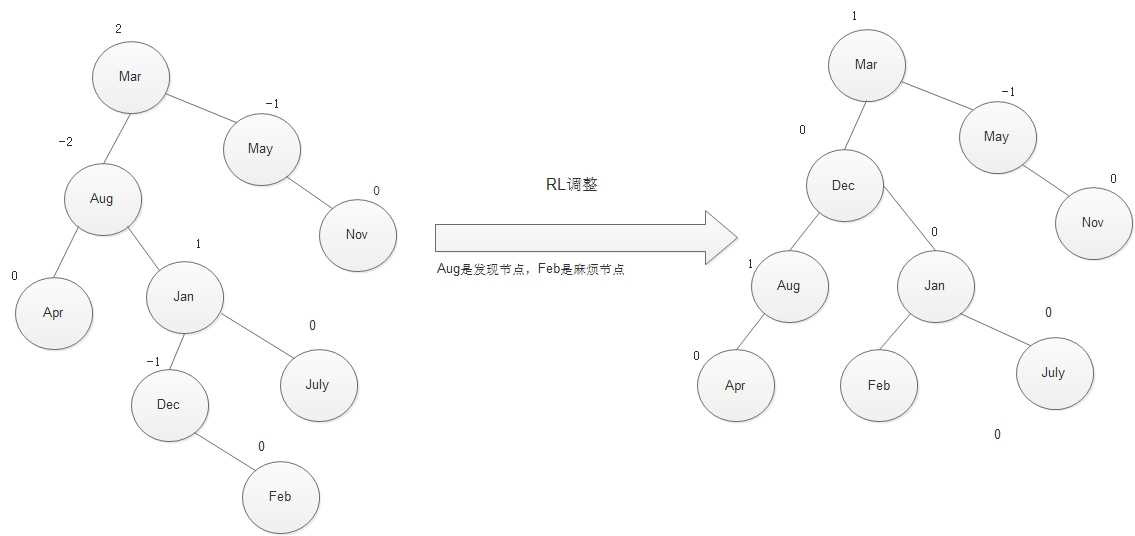
发现节点是Aug,麻烦节点是Feb,Feb在Aug的右子树的左子树上面,因而叫做RL插入,需要进行RL旋转
RL调整的通解图:
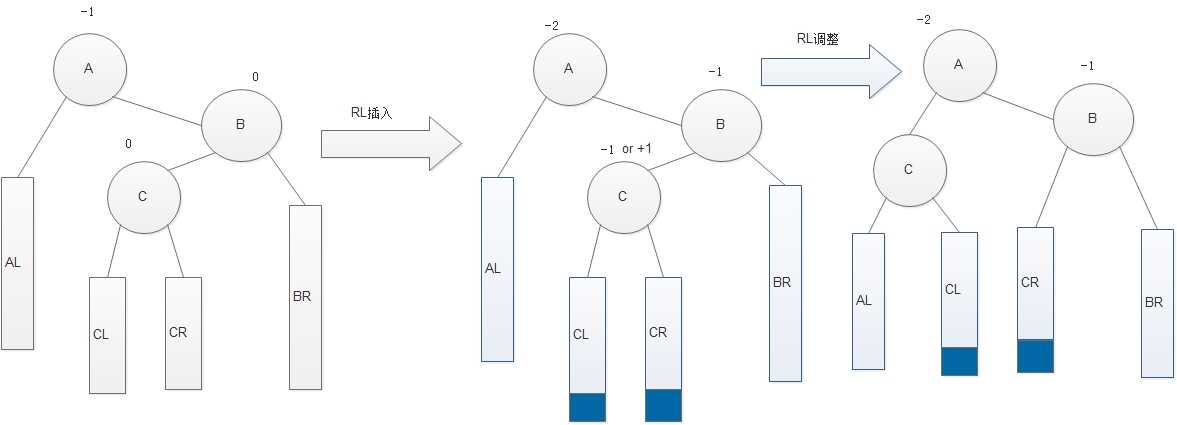
下面是二叉搜索树的相关操作的代码:

1 #include<stdio.h> 2 #include<stdlib.h> 3 4 typedef int elementType; 5 6 /*define a binary tree*/ 7 typedef struct node{ 8 elementType element; 9 struct node *left; 10 struct node *right; 11 int treeHeight;/*为了平衡二叉树计算方便,定义树高*/ 12 }tre,*pTree; 13 14 /*二叉搜索树的递归查找*/ 15 pTree find(elementType element,pTree tree){ 16 if(!tree){ 17 return NULL; 18 } 19 if(element<tree->element){ 20 /*查找元素比根元素小在左子树中查找*/ 21 return find(element,tree->left); 22 }else if(element>tree->element){ 23 /*查找元素比根元素小在右子树中查找*/ 24 return find(element,tree->right); 25 }else{/*找到该节点,返回*/ 26 return tree; 27 } 28 } 29 30 /*因为递归方法执行的效率低,而且上面的尾递归函数可以改写为递归函数*/ 31 pTree find2(elementType element,pTree tree){ 32 pTree temp; 33 temp = tree; 34 while(temp){ 35 if(element<temp->element){ 36 temp=temp->left; 37 }else if(element>temp->element){ 38 temp=temp->right; 39 }else{ 40 return temp; 41 } 42 } 43 return NULL; 44 } 45 46 /*根据二叉搜索树的特点,最小元素在最左边的节点上面*/ 47 pTree getMinElement(pTree tree){ 48 if(tree){ 49 while(tree->left){ 50 tree=tree->left; 51 } 52 } 53 54 return tree; 55 } 56 57 /*获取二叉搜索树中的最大元素,最大元素的位置应该在最右边的节点上*/ 58 pTree getMaxElement(pTree tree){ 59 if(tree){ 60 while(tree->right){ 61 tree = tree->right; 62 } 63 } 64 65 return tree; 66 } 67 68 /*二叉搜索树的插入,知识遵循二叉搜索树的性质,但是并没有调节平衡*/ 69 pTree insert(pTree tree,elementType element){ 70 pTree temp; 71 if(!tree){ 72 tree = (pTree)malloc(sizeof(tre)); 73 tree->element=element; 74 tree->left=tree->right=NULL; 75 }else{/**/ 76 if(element<tree->element){ 77 tree ->left = insert(tree->left,element); 78 } 79 else if(element>tree->element){ 80 tree->right = insert(tree->right,element); 81 } 82 } 83 return tree; 84 } 85 86 /*非递归的二叉搜索树的算法*/ 87 pTree insert2(pTree tree,elementType element){ 88 pTree temp; 89 int flag; 90 pTree parent; 91 if(!tree){ 92 tree = (pTree)malloc(sizeof(tre)); 93 tree->element=element; 94 tree->left=tree->right=NULL; 95 }else{ 96 temp=tree; 97 while(temp!=NULL){ 98 if(element<temp->element){ 99 //printf("lala\n"); 100 parent = temp; 101 temp=temp->left; 102 flag=0; 103 }else if(element>temp->element){ 104 parent = temp; 105 flag=1; 106 temp=temp->right; 107 } 108 } 109 110 temp = (pTree)malloc(sizeof(tre)); 111 temp->element=element; 112 temp->left=temp->right=NULL; 113 if(flag){ 114 parent->right=temp; 115 }else{ 116 parent->left=temp; 117 } 118 } 119 120 return tree; 121 } 122 123 /*在二叉搜索树中删除一个元素 124 算法思想: 125 1.首先查找到该元素 126 2.如果该元素是叶子节点,直接删除 127 3.如果该元素有一个孩子节点,直接把孩子节点挂载到该节点的父节点上 128 4.如果该节点有两个孩子,由两种方法 129 a.在该节点的左子树中找到最大元素节点T,把该节点的值替换成T的值,然后执行对T的删除操作 130 b.在该节点的右子树中找最小元素的节点T,把该节点的值替换为T的值,然后执行对T的删除操作 131 注:找最大或者最小元素是因为最大最小元素是叶子节点或者只有一个孩子。 132 */ 133 pTree deleteElement(pTree tree,elementType element){ 134 pTree temp; 135 if(!tree){ 136 printf("the element don‘t search in this tree\n"); 137 }else if(element<tree->element){ 138 tree->left=deleteElement(tree->left,element); 139 }else if(element>tree->element){ 140 tree->right = deleteElement(tree->right,element); 141 }else{//找到需要删除的元素节点 142 if(tree->left && tree->right){//该有两个孩子节点 143 temp = getMinElement(tree->right);/*获取右子树的最小值节点*/ 144 tree->element=temp->element; 145 tree->right=deleteElement(tree->right,temp->element); 146 }else{ 147 temp=tree; 148 if(!tree->left){ 149 tree=tree->right; 150 }else if(!tree->right){ 151 tree=tree->left; 152 } 153 free(temp); 154 } 155 } 156 return tree; 157 } 158 159 /*使用非递归的方法 160 pTree deleteElement2(pTree tree,elementType element){ 161 pTree temp,maxSubNode,flag,temp2; 162 if(!tree){ 163 printf("the tree is empty,don‘t allow delete elememt\n"); 164 }else{ 165 temp = find(element,tree); 166 if(temp==NULL){ 167 printf("the element don‘t exsit in this tree\n"); 168 }else{ 169 if(temp->left && temp->right){ 170 maxSubNode = getMinElement(temp->right); 171 temp->element = maxSubNode->element; 172 }else{ 173 maxSubNode = temp; 174 } 175 176 temp2=maxSubNode; 177 if(!maxSubNode->left){ 178 maxSubNode=maxSubNode->right; 179 }else if(!maxSubNode->right){ 180 maxSubNode=maxSubNode->left; 181 } 182 free(temp2); 183 } 184 185 } 186 return tree; 187 }*/ 188 189 190 //先序遍历 191 void preOrderTraversal(pTree tree){ 192 if(tree){ 193 printf("%d ",tree->element); 194 preOrderTraversal(tree->left); 195 preOrderTraversal(tree->right); 196 } 197 } 198 199 /*=====================================调整树为平衡二叉树===============================================*/ 200 201 int getMaxValue(int a,int b){ 202 return a > b ? a : b ; 203 } 204 205 /*获取二叉树的树高*/ 206 int getHeight(pTree tree){ 207 int leftHeight,rightHeight; 208 if(tree){ 209 leftHeight = getHeight(tree->left); 210 rightHeight = getHeight(tree->right); 211 return (leftHeight>rightHeight ? leftHeight : rightHeight)+1; 212 } 213 return 0; 214 } 215 /* 216 左单旋操作:将A与B进行LL旋转,并更新A和B的新高度,返回新的根节点B 217 A必须有一个左子节点B 218 */ 219 pTree singleLeftRatation(pTree A){ 220 pTree B = A->left; 221 A->left=B->right; 222 B->right = A; 223 A->treeHeight = getMaxValue(getHeight(A->left),getHeight(A->right))+1; 224 B->treeHeight = getMaxValue(B->left,A->treeHeight)+1; 225 return B; 226 } 227 228 /*右单旋:将A与B进行RR旋转,并更新A与B的高度,返回新的根节点B 229 注:A必须有一个右节点B 230 */ 231 pTree singleRightRatation(pTree A){ 232 pTree B = A->right; 233 A->right = B->left; 234 B->left = A; 235 A->treeHeight = getMaxValue(getHeight(A->left),getHeight(A->right))+1; 236 B->treeHeight = getMaxValue(getHeight(B->right),A->treeHeight); 237 return B; 238 } 239 240 /* 241 将A做LR旋转,返回新的根节点C 242 A必须有一个左自己的B,B必须有一个右子节点C 243 */ 244 pTree doubleLeftRightRatation(pTree A){ 245 /*先对B,C进行RR旋转,C被返回*/ 246 A->left = singleRightRatation(A->left); 247 /*在对A和C进行LL旋转,返回新的根节点C*/ 248 return singleLeftRatation(A); 249 } 250 251 /* 252 对A进行RL旋转,返回新的根节点C 253 注:A必须有一个右子节点B,B必须有一个左子节点C 254 */ 255 pTree doubleRightLeftRatation(pTree A){ 256 /*先对B,C进行LL旋转,返回新的根节点C*/ 257 A->right = singleLeftRatation(A->right); 258 /*在对A,C进行RR旋转,返回新的根节点C*/ 259 return singleRightRatation(A); 260 } 261 262 /*对二叉搜索树进行插入,插入后调整树的平衡*/ 263 pTree AVLInsert(pTree tree,elementType element){ 264 if(!tree){ 265 tree = (pTree)malloc(sizeof(tre)); 266 tree->element = element; 267 tree->left=tree->right = NULL; 268 tree->treeHeight=0; 269 }else if(element<tree->element){ 270 tree->left = AVLInsert(tree->left,element); 271 //判断平衡因子是否等于2 272 if(getHeight(tree->left)-getHeight(tree->right) == 2){ 273 if(element<tree->left->element){//element往tree的左子树的左子树插入导致平衡因子大于2,进行LL调整的 274 tree = singleLeftRatation(tree); 275 }else{//element往tree的左子树的右子树插入导致平衡因子大于2,进行LR调整 276 tree = doubleLeftRightRatation(tree); 277 } 278 } 279 }else if(element>tree->element){ 280 tree->right = AVLInsert(tree->right,element); 281 //判断平衡因子是否等于2 282 if(getHeight(tree->right)-getHeight(tree->left) == 2){ 283 if(element>tree->right->element){//element往tree的右子树的右子树插入导致平衡因子大于2,进行RR调整 284 tree = singleRightRatation(tree); 285 }else{//element往tree的右子树的左子树插入导致平衡因子大于2,进行RL调整 286 tree = doubleRightLeftRatation(tree); 287 } 288 } 289 }/* else 如果找到了,就不进行插入*/ 290 291 tree->treeHeight = getMaxValue(getHeight(tree->left),(getHeight(tree->right)))+1; 292 return tree; 293 } 294 295 296 void main(){ 297 printf("\n==========普通插入=====================================\n"); 298 int findElement=33; 299 int deleteData=41; 300 pTree tree=insert(NULL,30); 301 tree=insert(tree,15); 302 tree=insert(tree,41); 303 tree=insert(tree,33); 304 tree=insert(tree,50); 305 tree=insert(tree,35); 306 preOrderTraversal(tree); 307 printf("\n"); 308 printf("The find element is:%d,the result is %d \n",findElement,find(findElement,tree)->element); 309 printf("The min element:%d\n",getMinElement(tree)->element); 310 printf("The max element:%d\n",getMaxElement(tree)->element); 311 //printf("delete the elemet %d\n",deleteData); 312 //deleteElement(tree,deleteData); 313 printf("\nordinary tree preOrder\n"); 314 preOrderTraversal(tree); 315 316 printf("\n==========AVL插入=====================================\n"); 317 318 pTree AVLTree=AVLInsert(NULL,30); 319 AVLTree=AVLInsert(AVLTree,15); 320 AVLTree=AVLInsert(AVLTree,41); 321 AVLTree=AVLInsert(AVLTree,33); 322 AVLTree=AVLInsert(AVLTree,50); 323 AVLTree=AVLInsert(AVLTree,35); 324 printf("\n"); 325 printf("The find element is:%d,the result is %d \n",findElement,find(findElement,AVLTree)->element); 326 printf("The min element:%d\n",getMinElement(AVLTree)->element); 327 printf("The max element:%d\n",getMaxElement(AVLTree)->element); 328 //printf("delete the elemet %d\n",deleteData); 329 //deleteElement(AVLTree,deleteData); 330 printf("\nAVL tree preOrder\n"); 331 preOrderTraversal(AVLTree); 332 333 }
依次插入 30 15 41 33 50 35
则
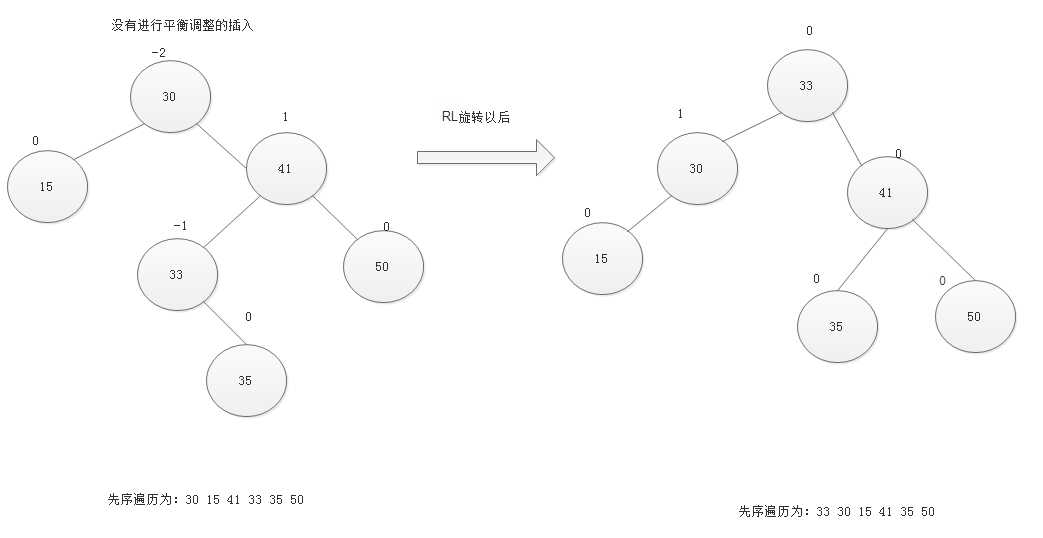
这个和程序运行的结果是一致的:
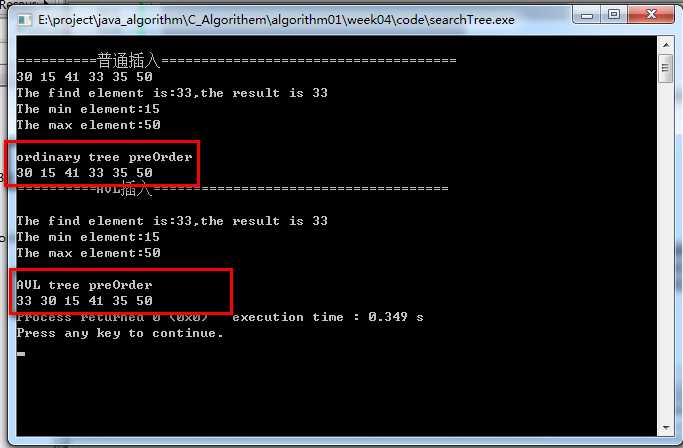
标签:树的定义 删除 .com uri 算法思想 实现 this 方法 bin
原文地址:http://www.cnblogs.com/yghjava/p/6715732.html