标签:大于 logs 模型 使用 最小 str 空间 问题 表达式
1、表示定理的证明
如果你求解的是L2-regularized的问题,那么一定有一个最好的w可以表示成z的线性组合:
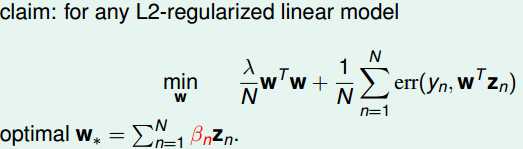
如何来证明这件事情呢?
我们将w分成两个部分,分别为w的平行部分(由zn展开的那个空间的向量来构成)和w的垂直部分(与zn展开表示的向量垂直的向量)。
我们希望最后完全没有w的垂直部分。
将最优的那个w与zn相乘其实和w的平行部分和zn相乘得到的结果是一样的,因为w的垂直部分与zn相乘为0,所以得到的err是一样的。
对于最佳解wTw,其包含w的平行部分的平方和w的垂直部分的平方,如果使用反证法,假设w的垂直部分不是0,那么,wTw必将大于w的平行部分的平方,但是最小解wTw却比w的平行部分的平方还大,这与我们的假设是矛盾的,所以就证明了w的垂直部分为0。
这样就证明了w的最佳解可以被z线性表达。

通过上面的证明,我们知道只要是求解L2的线性模型,就可以使用核技巧。
2、 将核函数用于逻辑回归
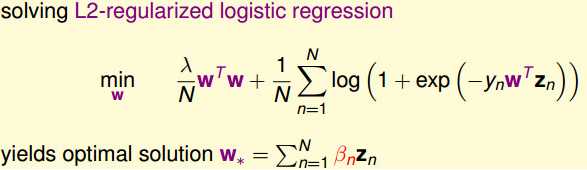
我们先得到要求解的表达式,然后用zn和βn的线性组合的方式表示最佳的w,代入到原始的式子中,就可以通过求βn代替求w了。
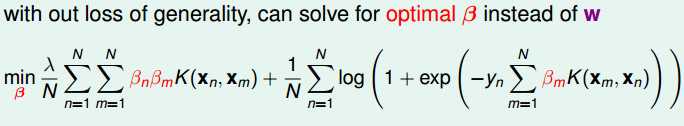
这就得到了一个没有约束条件的最佳化问题,我们可以通过梯度下降的方法来求解βn。这就是核逻辑回归问题。
标签:大于 logs 模型 使用 最小 str 空间 问题 表达式
原文地址:http://www.cnblogs.com/daguankele/p/6718141.html