标签：des style blog http color os 使用 io strong
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 14468 | Accepted: 5227 |
Description
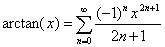(其中0 <= x <= 1) 公式(1) Input
Output
Sample Input
1
Sample Output
5
Source
1/a = (1/b + 1/c)/ (1 - 1/(b*c)) => bc-1 = a(b+c) assume b=a+m and c=a+n (b and c is always bigger than a) (a+m)(a+n)-1=a(a+m+a+n) => a*a+a*n+a*m+m*n-1=2*a*a+m*a+n*a => m*n=a*a+1
再枚举m(或者n)即可
关键是b=a+m,c=a+n这里的一个转换
1 #include<cstdio> 2 #include<cmath> 3 #include<cstring> 4 #include<stdlib.h> 5 #include<algorithm> 6 #define LL __int64 7 using namespace std; 8 int main() 9 { 10 //freopen("in.txt","r",stdin); 11 LL a; 12 scanf("%I64d",&a); 13 for(LL i=a;i>=0;i--)//枚举m 14 { 15 if((a*a+1)%i==0)//n=(a*a+1)/i m=i 16 { 17 printf("%I64d\n",a+i+a+(a*a+1)/i); 18 break; 19 } 20 } 21 return 0; 22 }
标签：des style blog http color os 使用 io strong
原文地址：http://www.cnblogs.com/clliff/p/3932970.html
