标签:屏幕 9.png 定义 位置 code 中序遍历 依次 中序 使用
树是由\(n (n \ge 0)\)个节点组成的有限集合(记为\(T\))。其中如果\(n=0\),它是一棵空树;如果\(n \gt 0\),这 \(n\)个节点中存在一个节点作为树的根节点,其余节点可分为\(m (m \ge 0)\)个互不相交的有限集\(T_1、T_2、...T_m\),其中每个集合本身又是一棵树,称为根节点的子树。「递归定义」
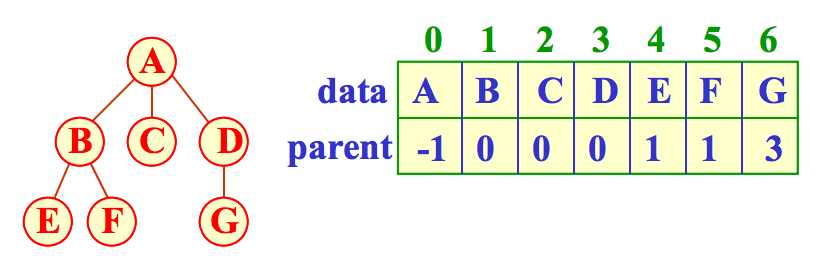 ?
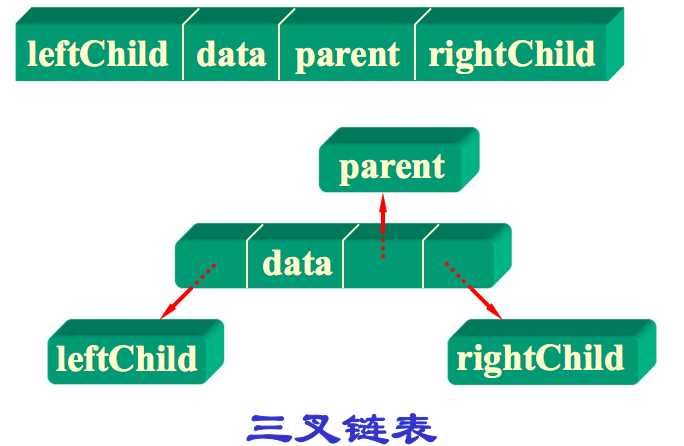
利用了每个节点(根节点除外)只有唯一双亲节点的性质。这种存储结构中,求某个节点的双亲节点的时间复杂度为\(O(1)\),求某个节点的孩子节点的时间复杂度为 \(O(n)\)
?
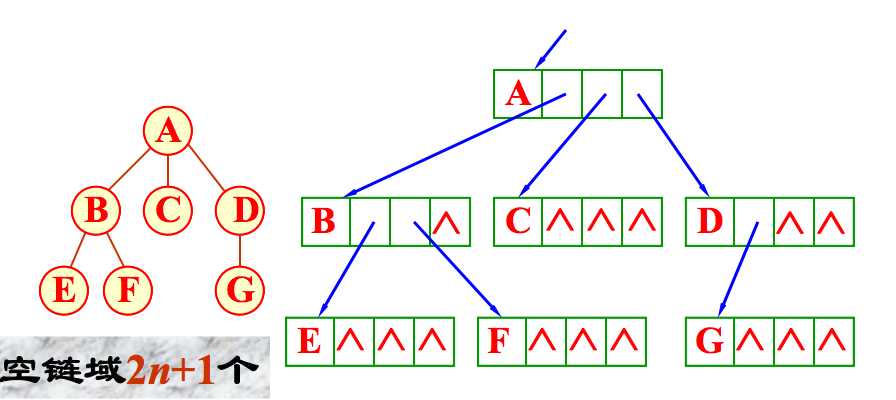
利用了每个节点(根节点除外)只有唯一双亲节点的性质。这种存储结构中,求某个节点的双亲节点的时间复杂度为\(O(1)\),求某个节点的孩子节点的时间复杂度为 \(O(n)\) ?
?
 ?
? ?
?
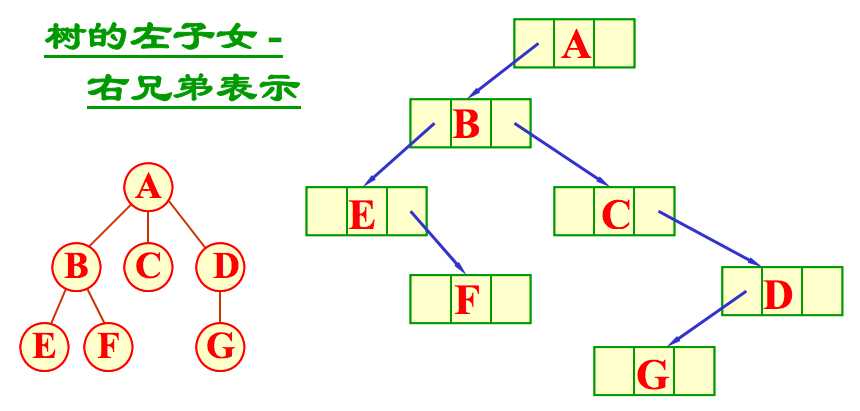 ?
?先根遍历:先访问根节点,再按照从左到右的次序先根遍历该根节点的每一个子树:
 ?
?
后根遍历:先按照从左到右的次序后根遍历根节点的每一棵子树,再访问根节点。
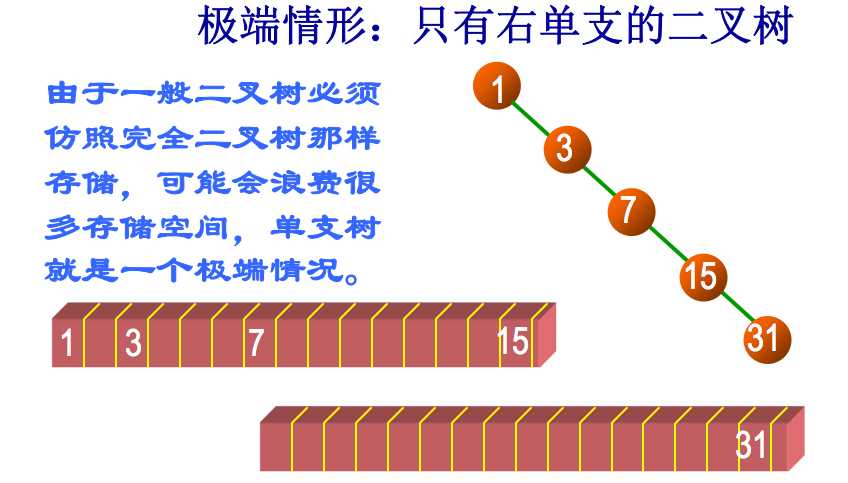
二叉树是由 \(n (n \ge 0)\) 个节点的有限集合,该集合或者为空集
,或者由一个根节点和两棵互不相交的、分别称为根节点的左子树和右子树的二叉树组成。
 ?
?
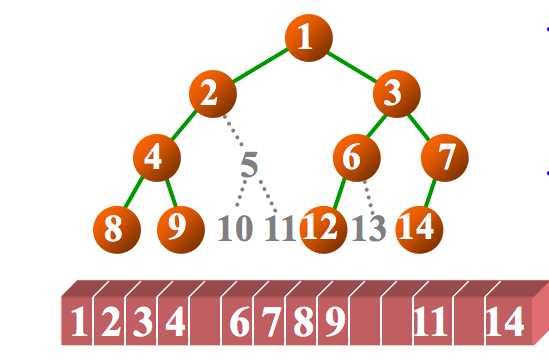
二叉树的性质
 ?
? ?
?
 ?
?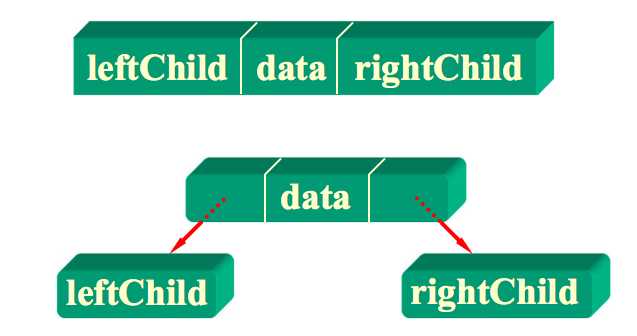 ?
?
 ?
? ?
? ?
?
 ?
?中根(中序)遍历:
 ?
?
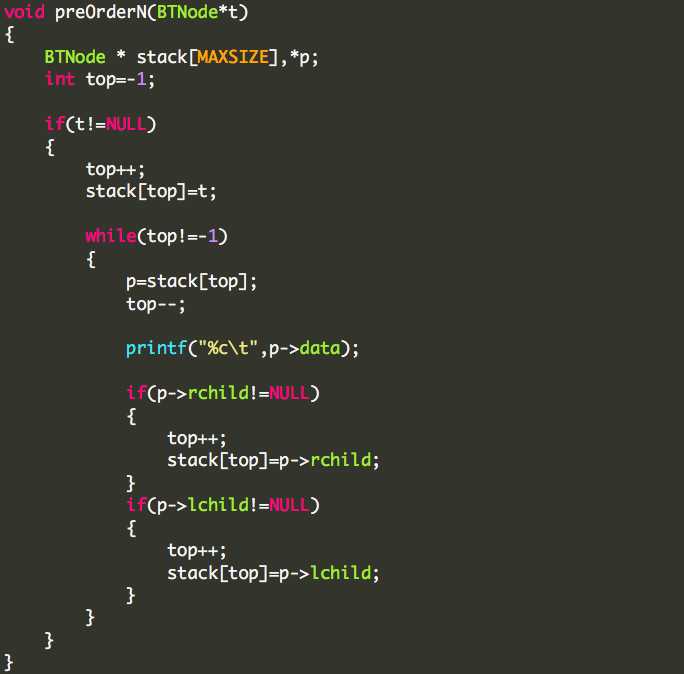
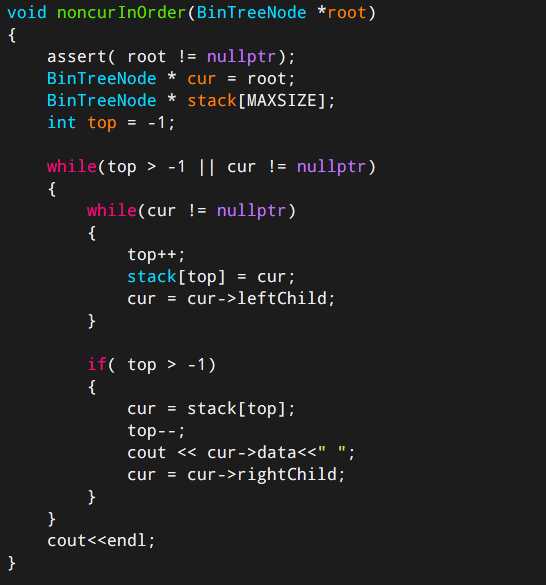
中序遍历的非递归实现:先扫描(并非访问)根节点的所有左节点并将它们一一进栈。然后出栈一个节点p,显然p没有左孩子节点或者左孩子节点已经访问过了,则访问它,然后扫描该右孩子节点的所有左孩子节点并一一进栈,如此继续直到栈空为止。
 ?
?
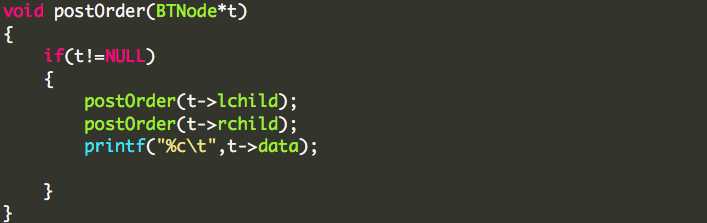
后根(后序) 遍历:
 ?
?
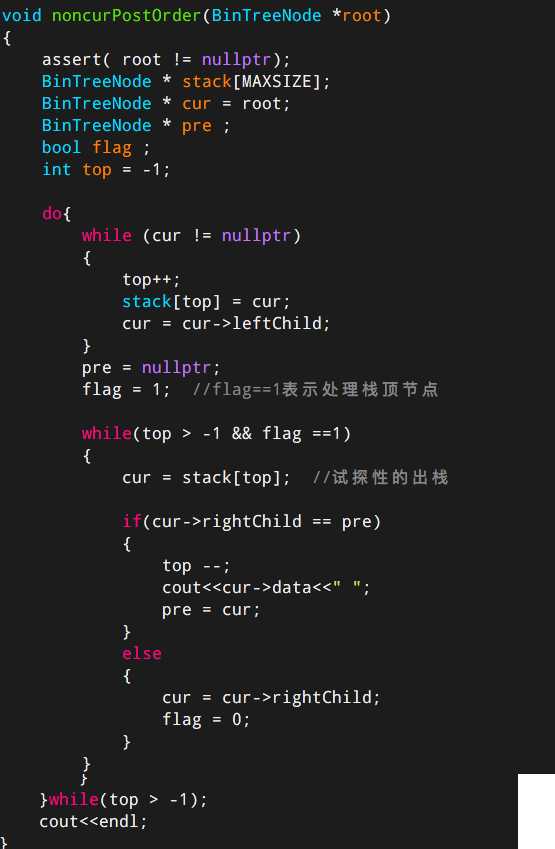
后序遍历的非递归实现:先扫描根节点的所有左节点并一一进栈,扫描完之后出栈一个节点*p,即当前节点,然后扫描该节点的右孩子节点并进栈,再扫描该右孩子的节点的所有左节点并进栈。当一个节点的左、右孩子节点均访问后再访问该节点,如此反复,直到栈空为止。
难点是怎么判断一个节点的右孩子节点已经访问过?,不妨使用q来保存右子树中刚刚被访问的节点(初值为NULL),若此时满足p->rchild==q成立,说明此时p的左右孩子均已访问,现在应该访问p节点。
 ?
?
标签:屏幕 9.png 定义 位置 code 中序遍历 依次 中序 使用
原文地址:http://www.cnblogs.com/halox/p/shu-de-ji-ben-gai-nian.html