标签：ati not 决策 变换 == tin 计算 float 切割
作者：桂。
时间：2017-04-20 18:31:37
链接：http://www.cnblogs.com/xingshansi/p/6740308.html
前言
本文为《统计学习方法》第四章：朴素贝叶斯（naive bayes），主要是借助先验知识+统计估计，本文主要论述其分类的思路。全文包括：
1）模型描述
2）算法求解
3）理论应用
内容为自己的学习记录，其中参考他人的地方，最后一并给出链接。
一、模型描述
A-理论框架
日常生活中，总会这么表达：“我觉得吧....”，“以我的经验来看,.....”，虽然有时候不靠谱，但它至少说明了一个认知上的问题：历史经验（数据）是有价值的。比如这样一个场景：
在我观念里，不同地区的人是这样的：
欧美人：鼻子-高，眼睛-蓝，表情-爱笑，饮食-喜欢西餐。
亚洲人：鼻子-低，眼睛-棕，表情-严肃，饮食-喜欢烧烤。
今天我在电视上又看到一个人：鼻子高高的，眼睛棕色的，表情是严肃的，我觉得吧...她可能是亚洲人。
可这里边的理论依据是什么呢？
对于训练数据集：
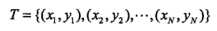
其中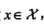
为输入的特征向量，
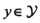为对应的类别。通过数据集可以获取一些先验知识（通常由统计得到）：
例如，类别信息：人群中亚洲人、欧美人的比例：
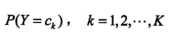
以及对应的条件概率，不同类别的特征信息：如欧美人中，高鼻子、爱笑、喜欢西餐....的概率：
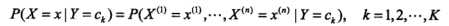
但这样的组合数太多了，给比如N个样本，每个10个特征，就是N10种可能（有点大），而且另一方面，欧美人鼻子高不高，与他喜不喜欢西餐、爱不爱笑，很可能是相互独立的，所以Bayes作了一个比较强的假设——条件分布独立性假设：
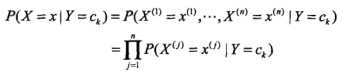
这个时候的计算量为10*N，小了很多，而且条件概率也更容易借助统计得出。借助已有信息得出的类别信息、不同类别的特征信息，就是我们的经验。
回到开始的问题：来了一个人，鼻子高高的，眼睛棕色的，表情是严肃的，这是哪里人呢？朴素贝叶斯不像昨天说的最近邻KNN（KNN的观点：不是亚洲人就是欧美人），朴素贝叶斯的说法是：这个人更可能是**人，这个可能就是概率，对应就是贝叶斯概率估计：
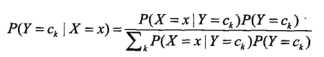
上面的公式直观理解就是：在给定特征下，Y不同类别的概率，特征不就是鼻子、微笑、饮食这些么，是已知的，Y对应类别，也就是欧美/亚洲人，这就完成了依靠经验的判断。
观察到上面的公式可以进一步简化：
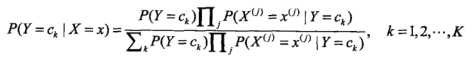
由于分母都是不变的，求解问题进一步变为：
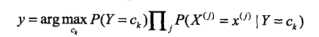
求解概率最大的类别，就是最终结果，至此完成了朴素贝叶斯的分类问题。
B-概率最大化与误差最小化的等价性
对于0-1风险函数：
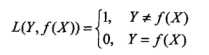
其中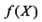
是分类决策函数，可以得出：
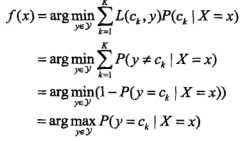
这与朴素贝叶斯原始问题是一致的，即概率最大化（贝叶斯估计）与误差（0-1风险函数）最小化具有等价性。
C-参数估计
这个其实上文已经提到了，就是利用已有的训练数据进行统计，得到的频率估计就当作概率估计，对应也可通过最大似然估计得出，直接给出公式（类别信息）：
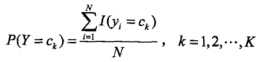
以及条件概率（不同类别下的特征信息）：
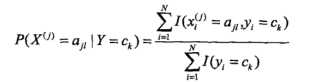
其中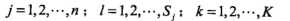
，
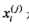是第i个样本第j个特征，
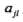是第j个特征可能取的第l个值，I为指示函数。
至此完成了参数估计。
D-参数修正
再回顾朴素贝叶斯的准则函数：
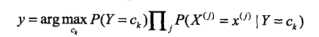
表达式有概率的连乘，一个小的数*一个大的数，结果可能大、可能小，但0*一个大的数=0，这样一巴掌拍死是不合适的，因此希望对估计的参数修正一下，用的是additive smoothing方法，直接给出wikipedia的内容：
对应上面的最大似然估计，参数修正为：
类别信息：
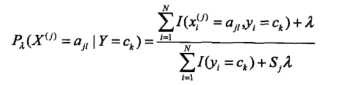
不同类别的特征信息：
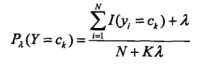
容易验证，它们仍然是一种概率存在，至此完成参数修正（不是唯一修正方法哦~）。
二、算法求解
A-算法步骤
直接给出算法步骤：
B-算法步骤细说
书中给出了两个例子：参数未修正、参数修正，两种场景的估计，都是三步走，一样的套路。
问题描述：
参数未修正：
第一步：类别信息
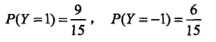
第二步：不同类别的特征信息
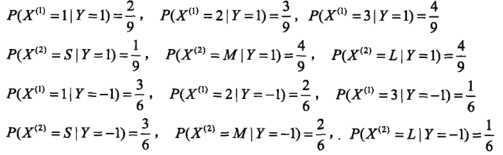
第三步：不同类别概率估计
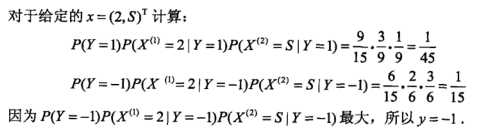
参数修正：这里
。
第一步：类别信息
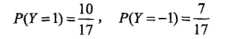
第二步：不同类别的特征信息
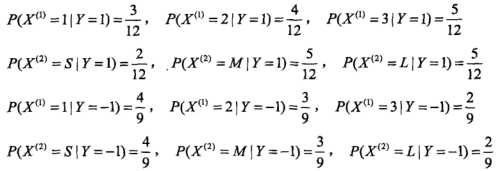
第三步：不同类别概率估计
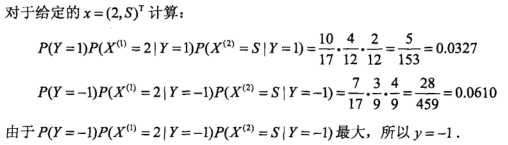
三、理论应用
介绍一个简单的小应用：恶意留言过滤。
原始数据集：
首先载入数据集，数据集一般爬取并切割分词得到：
from numpy import *
def loadDataSet():
postingList=[[‘my‘, ‘dog‘, ‘has‘, ‘flea‘, ‘problems‘, ‘help‘, ‘please‘],
[‘maybe‘, ‘not‘, ‘take‘, ‘him‘, ‘to‘, ‘dog‘, ‘park‘, ‘stupid‘],
[‘my‘, ‘dalmation‘, ‘is‘, ‘so‘, ‘cute‘, ‘I‘, ‘love‘, ‘him‘],
[‘stop‘, ‘posting‘, ‘stupid‘, ‘worthless‘, ‘garbage‘],
[‘mr‘, ‘licks‘, ‘ate‘, ‘my‘, ‘steak‘, ‘how‘, ‘to‘, ‘stop‘, ‘him‘],
[‘quit‘, ‘buying‘, ‘worthless‘, ‘dog‘, ‘food‘, ‘stupid‘]]
classVec = [0,1,0,1,0,1] #1 is abusive, 0 not
return postingList,classVec
这里类别为两类，1-恶意留言；0-非恶意留言。
因为是通过关键词判断，因此进一步简化数据集：利用 | 以及 set 将数据集重复部分删除，构建vocabulary list:
def createVocabList(dataSet):
vocabSet = set([]) #create empty set
for document in dataSet:
vocabSet = vocabSet | set(document) #union of the two sets
return list(vocabSet)
有了数据集，还是文本信息，需要将其转换成数字信息，这样才可以进行统计。
def setOfWords2Vec(vocabList, inputSet):
returnVec = [0]*len(vocabList)
for word in inputSet:
if word in vocabList:
returnVec[vocabList.index(word)] = 1
else: print "the word: %s is not in my Vocabulary!" % word
return returnVec
三步走就可以走两步了。第一步：计算类别信息，第二步：计算不同类别的特征信息。在计算之前，有两点小trick:
If any of these numbers are 0, then when we multiply them together we get 0. To lessen the impact of this, we’ll initialize all of our occurrence counts to 1, and we’ll initialize the denominators to 2. 因为在set 和 | 操作中，不免删除了一些单词，导致一些概率为0，这是不希望看到的，考虑到是两类，初始时 各类进行1次累加，总的进行2次累加；
- 为了防止数值溢出，采用Log(.)变换；即：
前两步走对应的code:
def trainNB0(trainMatrix,trainCategory):
numTrainDocs = len(trainMatrix)
numWords = len(trainMatrix[0])
pAbusive = sum(trainCategory)/float(numTrainDocs)
p0Num = ones(numWords); p1Num = ones(numWords) #change to ones()
p0Denom = 2.0; p1Denom = 2.0 #change to 2.0
for i in range(numTrainDocs):
if trainCategory[i] == 1:
p1Num += trainMatrix[i]
p1Denom += sum(trainMatrix[i])
else:
p0Num += trainMatrix[i]
p0Denom += sum(trainMatrix[i])
p1Vect = log(p1Num/p1Denom) #change to log()
p0Vect = log(p0Num/p0Denom) #change to log()
return p0Vect,p1Vect,pAbusive
对应调用上面的函数就是：
import bayes
listOPosts,listClasses = bayes.loadDataSet()
myVocabList = bayes.createVocabList(listOPosts)
trainMat=[]
for postinDoc in listOPosts:
trainMat.append(bayes.setOfWords2Vec(myVocabList, postinDoc))
p0V,p1V,pAb=bayes.trainNB0(trainMat,listClasses) #Step1 Step2
测试数据集：
同样首先对文本预处理，与训练数据处理类似，文本转换为数字：
testEntry = [‘stupid‘, ‘garbage‘] thisDoc = array(bayes.setOfWords2Vec(myVocabList, testEntry))
预处理完之后，下面就是第三步了：利用测试数据的特征，进行类别概率的计算。
def classifyNB(vec2Classify, p0Vec, p1Vec, pClass1):
p1 = sum(vec2Classify * p1Vec) + log(pClass1) #element-wise mult
p0 = sum(vec2Classify * p0Vec) + log(1.0 - pClass1)
if p1 > p0:
return 1
else:
return 0
哪家概率大，就判给哪个类别。对应测试code:
print testEntry,‘classified as: ‘,bayes.classifyNB(thisDoc,p0V,p1V,pAb)
测试结果为：1，即恶意留言，stupid/garbage 这与实际也是相符的。
参考：
标签：ati not 决策 变换 == tin 计算 float 切割
原文地址：http://www.cnblogs.com/xingshansi/p/6740308.html
