标签:独立 排序 color add append ase 存在 决策 需要
贝叶斯分类
贝叶斯最基本的思想就是条件概率公式+条件独立假设。
它的思想有点类似于奥卡姆剃刀原理,举个例子,当前眼前走过一个黑人的时候,为你他是那里人,你第一眼想到的是他是个非洲人。因为非洲人普遍皮肤黑。
贝叶斯分类思想与此类似,当问你某个数据实例属于某个类别时候,会先去求各个类别下出现该数据实例的概率是多少,那个类别下概率越大,就分为哪个类别。
条件概率公式:
P(xy) = P(y|x)*P(x) = P(x|y)*P(y)
=> P(y|x) = P(x|y)*P(y) / P(x)
而贝叶斯公式:当X是由一组完备的事件组成的时候,P(X) = P(x1)*...*P(xn)
对于给定特征向量X,它的类别为Yc:
Yc = max i P(Yi|X) = max i { P(X|Yi)*P(Yi)/P(X) }
即求在X条件下yi概率最大的类别 i 作为分类类别,由于等式右边的分母P(X),所以只用计算max i { P(X|Yi)*P(Yi) }
其中P(Yi)是每个类别的概率,即每个类别的在训练集中的频率
P(X|Yi)可以根据贝叶斯公式和条件独立假设展开,P(X|Yi) = P(x1|Yi) * P(x2|Yi) *...*P(xn|Yi)
其中P(xi|Yi)为当前类别yi下(所有类别为yi的数据实例),特征x取值为xi的概率(取值为xi的数据实例的频率)。
所以贝叶斯分类模型的训练只要计算好以下两个概率:
在Python中可以用嵌套字典这样表示模型训练要求的概率P(xi=val|Yi):
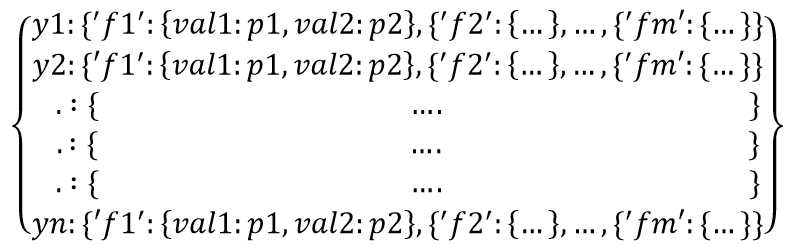
其中yi是各个类别,fi是当前类别yi下每一个特征,val是当前特征fi下的取值,pi是fi取值为pi的频率。有点绕口。。。
可以按照上面的数据结构,依次按yi、fi划分数据集,其实就是按行在按列切分数据集,然后求fi取各个值的概率。

上图中收入是预测的类别变量,后面三个是特征变量,对应求解过程就是,先按类别变量收入排序(划分数据),然后求收入yi=高(低)的时候,特征变量fi=能力(学历、性别)时候,取值val=高(中、低)的概率。概率用频率来估计。
#coding=uft-8
import os, sys from math import * import time #load dataSet def loadData(filePath): dataSet = [] with open(filePath) as fin: for line in fin: label_feats = line.strip().split(‘\t‘) #print label_feats dataSet.append(label_feats) labelList = [i[0] for i in dataSet] uniqLabel = list(set(labelList)) featuresNum = len(dataSet[0][1:]) features = [] for i in range(featuresNum): features.append(‘f‘+str(i+1)) #print uniqLabel #print features return dataSet,uniqLabel,features def calcPOfLabels(dataSet, labels): pOfLabels = [] total = len(dataSet) labelList = [example[0] for example in dataSet] labelsKinds = len(labels) for i in range(labelsKinds): pOfLabels.append(labelList.count(labels[i])) #pOfLabels[i] /= float(total) #laplacian correction pOfLabels[i] = (pOfLabels[i] + 1) / (float(total) + labelsKinds) print pOfLabels[i] return pOfLabels def getYi_Fi_ConditionP(subColumn, colIndex): yi_fi = {} uniqCol = set(subColumn) total = len(subColumn) for val in uniqCol: pinlv = 0 for d in subColumn: if(d == val): pinlv += 1 #yi_fi[val] = float(pinlv) / total #‘192‘:p if(colIndex != 10): yi_fi[val] = (float(pinlv) + 1)/ (total + 256) #laplacian correction else: yi_fi[val] = (float(pinlv) + 1)/ (total + 15672) #laplacian correction return yi_fi def getYi_Fs_ConditionP(subSet, features): yi_fs = {} for f in features: col = features.index(f) + 1 #subSet first col is label subColumn = [d[col] for d in subSet] #split subSet with feature yi_fs[f] = getYi_Fi_ConditionP(subColumn, col) #fi:{‘192‘:0.2, ‘202‘:0.4} return yi_fs def getYs_Fs_ConditionP(dataSet, labels, features): conditionP = {} for yi in labels: subSet = [] #split dataSet with yi for d in dataSet: if(d[0] == yi): subSet.append(d) conditionP[yi] = getYi_Fs_ConditionP(subSet, features) #yi:{‘f1‘:{}, ‘f2‘:{}},依次构建字典 return conditionP if(len(sys.argv) < 2): print ‘Usage xxx.py trainDataFile‘ sys.exit() t1 = time.time() dataSet, labels, features = loadData(sys.argv[1]) pOfLabels = calcPOfLabels(dataSet, labels) ys_fs_conditionP = getYs_Fs_ConditionP(dataSet, labels, features) print pOfLabels print ys_fs_conditionP t2 = time.time() print t2 - t1
得到P(xi|Yi)就可以求解当前数据实例条件下各个类别的条件概率,以此来预测分类。
ps:
1、代码实现过程中要注意拉普拉斯平滑。因为按照yi划分数据集后,可能某个特征的取值val不在当前类别的划分中;
虽然不在,但是我们不能不去求P(xi=val|Yi)的概率啊(测试集中可能会出现),而且也不能直接让P(xi=val|Yi)=0,需要用拉普拉斯平滑。
即让每个取值val都+1,那么分母也要加N,N是val的取值个数,这样可以保证概率和还是为1
上面的代码val取值不存在我就没有计算它的概率,我是在预测的时候计算了拉普拉斯平滑后的概率。
2、写了决策树和贝叶斯分类模型,感觉都是对数据集划分,然后用频率估计概率。重要的是怎么构建求解结果的数据结构。
标签:独立 排序 color add append ase 存在 决策 需要
原文地址:http://www.cnblogs.com/vincent-vg/p/6746256.html