３.空域图像处理的洪荒之力

标签：文档   归一化   处理   空间   blog   操作   ima   can   项目   

１.滤波以及边缘检测

１）空间滤波以及频域滤波

包括线性和非线性滤波

２）边缘检测

canny,Sobel,Laplace

项目：车牌识别运用到机器学习中的SVM以及NN（Ｎeural network）算法

一.获取的图像

图像包含噪声：

原因：１.源传感器的质量；２.光照变换;;3.量化过程引入噪声．

在图像处理当中把图像复原或者去噪称为图像滤波或者图像复原．这是我们拿到图像之后的第一步操作．受到噪声污染的图像叫做退化，去噪就称为复原．常见噪声为加性噪声（与信号的关系是相加的，不管有没有信号，噪声都是始终存在的）＼乘性噪声（由于信道不理想，它与信道的关系是相乘的，信号存在，乘性噪声就存在，反之就不存在）．把加性的随机性看成是系统的系统背景噪声，乘性的随机性噪声看成是系统的变性．

二.２Ｄ滤波　

在一维数据里面有噪声，首先想到的是做滑动平均，假设窗口采用的是５，那么每次都是对要去噪的改数据附近的５个值求平均，然后将平均后的值赋给该值．

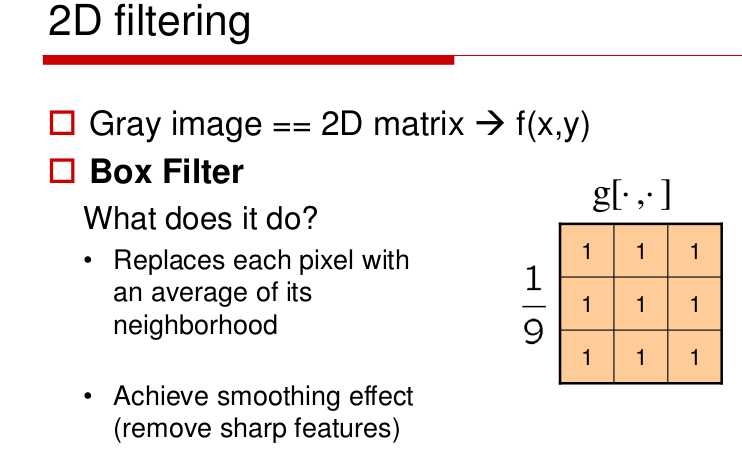
在二维里面对其进行展开，同样有一个滑动窗口，比如是３＊３的一个二维矩阵窗口，

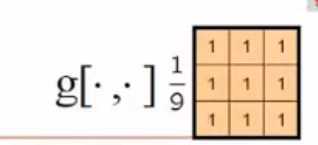
用这个滑动窗口对原始图像进行滑动滤波，对应位相乘，然后相加，再取平均，赋给中间那个值．注意千万不要在原始图像的基础上进行修改．

其过程如下：

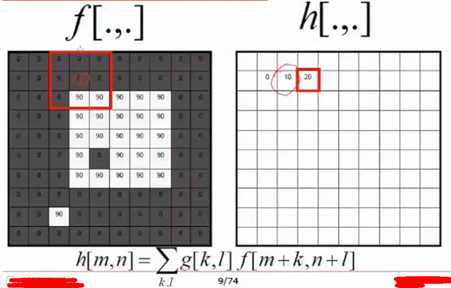
上面的滤波器叫做box filter，但是这样的滤波会有一些水纹或者说图像不是那么平滑有跳跃的感觉，如下

解释一下，在频域里面用的是一个矩形框来滤波，它在频域里面是一个类似于这样的函数

它在高频的时候是有跳跃的，它不是真正的低通滤波器．在某些高频的时候是可以通过的．

下面讲解一下真正的低通滤波器

先说一下在opencv中的两种滑动实现方式：Blur()和boxFilter()函数

在官方文档里面的解释是两种方式都一样，其实有一点不一样，boxFilter()是可以不用归一化的，而Blur()是必须归一化的．

在２Ｄ当中的卷积（Ｃonvolution in 2D）

跟之前的滑动并不一样，它公式是减号．如果对一个对称的boxfilter是没有影响的．只有对那些非对称的滑动窗口才不一样．总结如下

３.空域图像处理的洪荒之力

标签：文档   归一化   处理   空间   blog   操作   ima   can   项目   

原文地址：http://www.cnblogs.com/gary-guo/p/6752050.html