人大任务参考

标签：generator   which   sep   最小   pap   reg   例子   teacher   pos   

机器学习基本概念

机器学习、统计模型和数据挖掘有什么异同？

机器学习和统计模型区别不是很大，机器学习和统计模型中的回归都一样，底层算法都是差不多的，只是侧重点不一样，在统计学的角度，回归主要解决的问题侧重点在于模型的解释能力，关注的是 x 和 y 之间的关系，关注的更多是系数，从机器学习的角度看，关注的重点是预测的准确性。

机器学习和数据挖掘也没什么不一样，两者的算法基本上是一样的，只是在一些流程步骤上，数据挖掘会有一些特征工程的工作，以及对具体应用问题的解释。

有监督学习和无监督学习有什么区别？

有监督学习就是指有 y 作为数据的一部分，被称为目标变量，或被解释变量。无监督学习是指一堆数据，没有特定的 y，要从一堆 x 里找到模式或者规律出来。

有监督学习可以分为两个子类：分类和回归。分类问题中要预测的 y 偏离散，比如性别、血型；回归问题 y 都是连续的，实数域中的，比如收入、天气。

分类问题和聚类问题有什么区别？

分类问题是预测一个未知类别的对象属于哪个类别，而聚类是根据选定的指标，对一群对象进行划分，它不属于预测问题。

交叉验证是什么？

交叉验证是指用来建立模型的数据，和最后用来模型验证的数据，是不一样的。实践中拿到数据后，应该分为几个部分，最简单的分为两部分，一部分用于训练模型，另外一部分用于检验模型，这就是交叉验证。

何时用到特征工程？

特征工程是指要把原始数据做些整理，做些转换，主要目的是暴露出预测 y 的信息。

如何加载 sklearn 的内置数据集？

from sklearn import datasets
from sklearn import cross_validation
from sklearn import linear_model
from sklearn import metrics
from sklearn import tree
from sklearn import neighbors
from sklearn import svm
from sklearn import ensemble
from sklearn import cluster

%matplotlib inline
import matplotlib.pyplot as plt

import numpy as np
import seaborn as sns

skearn 有很多内置的数据集，上面已经加载了 sklearn 的 datasets，datasets 有一些可以用的数据，比如说加载 boston 数据集，加载后返回的就是个数据字典。

boston = datasets.load_boston()
print boston.keys()

[‘data‘, ‘feature_names‘, ‘DESCR‘, ‘target‘]

数据集的大小/格式/类型等信息如何得知？

print boston.DESCR

Boston House Prices dataset

Notes
------
Data Set Characteristics:  

    :Number of Instances: 506 

    :Number of Attributes: 13 numeric/categorical predictive
    
    :Median Value (attribute 14) is usually the target

    :Attribute Information (in order):
        - CRIM     per capita crime rate by town
        - ZN       proportion of residential land zoned for lots over 25,000 sq.ft.
        - INDUS    proportion of non-retail business acres per town
        - CHAS     Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)
        - NOX      nitric oxides concentration (parts per 10 million)
        - RM       average number of rooms per dwelling
        - AGE      proportion of owner-occupied units built prior to 1940
        - DIS      weighted distances to five Boston employment centres
        - RAD      index of accessibility to radial highways
        - TAX      full-value property-tax rate per $10,000
        - PTRATIO  pupil-teacher ratio by town
        - B        1000(Bk - 0.63)^2 where Bk is the proportion of blacks by town
        - LSTAT    % lower status of the population
        - MEDV     Median value of owner-occupied homes in $1000‘s

    :Missing Attribute Values: None

    :Creator: Harrison, D. and Rubinfeld, D.L.

This is a copy of UCI ML housing dataset.
http://archive.ics.uci.edu/ml/datasets/Housing


This dataset was taken from the StatLib library which is maintained at Carnegie Mellon University.

The Boston house-price data of Harrison, D. and Rubinfeld, D.L. ‘Hedonic
prices and the demand for clean air‘, J. Environ. Economics & Management,
vol.5, 81-102, 1978.   Used in Belsley, Kuh & Welsch, ‘Regression diagnostics
...‘, Wiley, 1980.   N.B. Various transformations are used in the table on
pages 244-261 of the latter.

The Boston house-price data has been used in many machine learning papers that address regression
problems.   
     
**References**

   - Belsley, Kuh & Welsch, ‘Regression diagnostics: Identifying Influential Data and Sources of Collinearity‘, Wiley, 1980. 244-261.
   - Quinlan,R. (1993). Combining Instance-Based and Model-Based Learning. In Proceedings on the Tenth International Conference of Machine Learning, 236-243, University of Massachusetts, Amherst. Morgan Kaufmann.
   - many more! (see http://archive.ics.uci.edu/ml/datasets/Housing)

boston.data # 自变量矩阵，面积、家具等特征

array([[  6.32000000e-03,   1.80000000e+01,   2.31000000e+00, ...,
          1.53000000e+01,   3.96900000e+02,   4.98000000e+00],
       [  2.73100000e-02,   0.00000000e+00,   7.07000000e+00, ...,
          1.78000000e+01,   3.96900000e+02,   9.14000000e+00],
       [  2.72900000e-02,   0.00000000e+00,   7.07000000e+00, ...,
          1.78000000e+01,   3.92830000e+02,   4.03000000e+00],
       ..., 
       [  6.07600000e-02,   0.00000000e+00,   1.19300000e+01, ...,
          2.10000000e+01,   3.96900000e+02,   5.64000000e+00],
       [  1.09590000e-01,   0.00000000e+00,   1.19300000e+01, ...,
          2.10000000e+01,   3.93450000e+02,   6.48000000e+00],
       [  4.74100000e-02,   0.00000000e+00,   1.19300000e+01, ...,
          2.10000000e+01,   3.96900000e+02,   7.88000000e+00]])

boston.data.shape

(506, 13)

boston.target.shape # 目标变量，房价

(506,)

datasets 除了现有的数据，还可以造一些数据，通过人造数据，来研究不同算法的特点。

datasets.make_regression

<function sklearn.datasets.samples_generator.make_regression>

回归问题

回归问题中，y 是个连续的数值，不仅可以采取线性回归，还可以使用决策树等做回归，只要输出是连续值，都可以用回归模型。

sklearn 的回归和 statsmodel 中的回归有什么异同？

如果使用同样的模型，两者的回归的解都是一样的，只是 statsmodel 输出更多些，比较偏向对参数做更多的解释，而 sklearn 更注重预测准确性。

如何使用交叉验证？它和过拟合有什么关系？

来个完整的例子。

np.random.seed(123)
X_all, y_all = datasets.make_regression(n_samples=50, n_features=50, n_informative=10)  # 真正有用的变量只有 10 个，另外 40 个都是噪音
print X_all.shape, y_all.shape

(50, 50) (50,)

这个数据集比较棘手，样本数比较少，变量多，容易过拟合，而且有用的变量不多，有很多噪音在里面，在做回归时，很容易把噪音放到方程里，用传统的方法比较难于处理，这里用机器学习处理。

为了防止过拟合，要用交叉验证，把数据分为两部分，一部分用于训练，一部分用于验证。

X_train, X_test, y_train, y_test = cross_validation.train_test_split(X_all, y_all, train_size=0.5)
print X_train.shape, y_train.shape
print X_test.shape, y_test.shape
print type(X_train)

(25, 50) (25,)
(25, 50) (25,)
<type ‘numpy.ndarray‘>

如何以线性模型拟合数据集？

model = linear_model.LinearRegression() # 实例化
model.fit(X_train, y_train) # 做线性回归拟合数据

LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)

残差（residual）是什么？如何评估模型是个好模型？

残差是真实的 y 和预测的 y 的差，残差越小，拟合越好。

def sse(resid):
    return sum(resid**2) # 残差平方和，是回归效果的一个指标

残差平方和是回归效果的一个指标，值越小，说明模型越好。

resid_train = y_train - model.predict(X_train)
sse_train = sse(resid_train)
print sse_train

5.87164948974e-25

resid_test = y_test - model.predict(X_test)
sse_test = sse(resid_test)
sse_test

194948.84691187815

model.score(X_train, y_train) # 计算判定系数 R-squared

1.0

model.score(X_test, y_test)

0.26275088549060643

模型在测试集上的分数只有 0.26，效果并不好。

画出各个样本对应的残差，和各个变量的系数。

def plot_residuals_and_coeff(resid_train, resid_test, coeff):
    fig, axes = plt.subplots(1, 3, figsize=(12, 3))
    axes[0].bar(np.arange(len(resid_train)), resid_train) # 各个样本对应的残差
    axes[0].set_xlabel("sample number")
    axes[0].set_ylabel("residual")
    axes[0].set_title("training data")
    axes[1].bar(np.arange(len(resid_test)), resid_test) # 各个样本对应的残差
    axes[1].set_xlabel("sample number")
    axes[1].set_ylabel("residual")
    axes[1].set_title("testing data")
    axes[2].bar(np.arange(len(coeff)), coeff) # 各个变量的系数
    axes[2].set_xlabel("coefficient number")
    axes[2].set_ylabel("coefficient")
    fig.tight_layout()
    return fig, axes

fig, ax = plot_residuals_and_coeff(resid_train, resid_test, model.coef_); # 训练集的残差，测试集的残差，各个系数的大小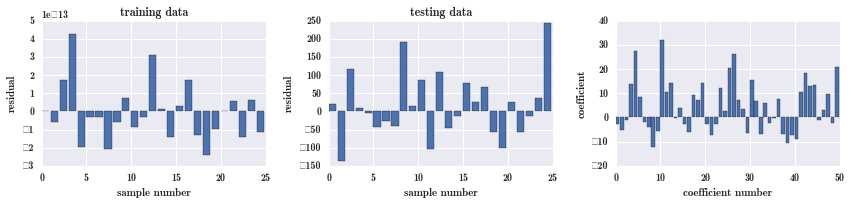

可以看到第一幅图训练集中的残差不算大，范围在 -3 到 5 之间，测试集的残差就过大，范围在 -150 到 250 之间，可见模型过拟合了，在训练集上还行，测试集上就很糟糕。

真实变量里只有 10 个是有用的，而上面的变量系数图有很多都不是 0，有很多冗余。变量多，样本少，怎么解决呢？

变量比样本多时，如何处理？

一种方法是做个主成分分析，降维，对变量做个筛选，再放到模型里来，但这种方法比较麻烦。

还有种是正则化的方法。

正则化是什么？有哪两种方法？

正则化在统计学里有两种思路，一种叫岭回归，把系数放到 loss function 中，经典的 loss function 是残差平方和，这里把 50 个系数平方求和，放到 loss function 中，所以最终既要使残差平方和小，又要使权重小，可以压制一些过于冗余的权重。

model = linear_model.Ridge(alpha=5) # 参数 alpha 表示对于权重系数的决定因子
model.fit(X_train, y_train)

Ridge(alpha=5, copy_X=True, fit_intercept=True, max_iter=None,
   normalize=False, random_state=None, solver=‘auto‘, tol=0.001)

resid_train = y_train - model.predict(X_train)
sse_train = sum(resid_train**2)
print sse_train

2963.35374445

resid_test = y_test - model.predict(X_test)
sse_test = sum(resid_test**2)
print sse_test

187177.590437

残差平方和还比较高。

model.score(X_train, y_train), model.score(X_test, y_test)

(0.99197132152011414, 0.29213988699168503)

之前测试集的 R 方是 0.26，这里是 0.29，略有改善。

fig, ax = plot_residuals_and_coeff(resid_train, resid_test, model.coef_)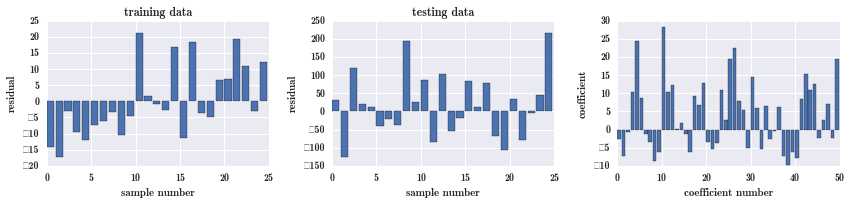

从图上看，training 的残差增加了，testing 的有所减少，系数大小没有太多改善，所以在这里使用岭回归有一点点效果，并不明显。

下面使用正则化的另一种方法，称为 Lasso，思路跟岭回归是一样的，都是把残差平方和以及系数放到 loss function 中，既要使残差平方和小，又要使系数小，但 Losso 公式有点不一样，Losso 是把权重的绝对值加起来，而岭回归是把权重的方法加起来，有这么一点不一样，就可以使得很多权重回为 0。看小效果。

model = linear_model.Lasso(alpha=1.0)
model.fit(X_train, y_train)

Lasso(alpha=1.0, copy_X=True, fit_intercept=True, max_iter=1000,
   normalize=False, positive=False, precompute=False, random_state=None,
   selection=‘cyclic‘, tol=0.0001, warm_start=False)

resid_train = y_train - model.predict(X_train)
sse_train = sse(resid_train)
print sse_train

256.539066413

resid_test = y_test - model.predict(X_test)
sse_test = sse(resid_test)
print sse_test

691.523154567

fig, ax = plot_residuals_and_coeff(resid_train, resid_test, model.coef_)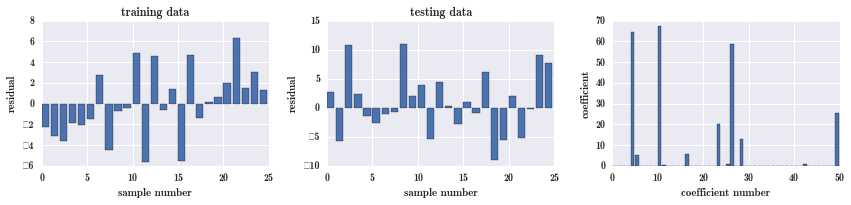

testing 的残差有明显的减小，范围减小到 -10 到 15 之间。很多系数也变为 0，真正的起作用的只有少数几个。这是 lasso 的优点，它可以应付有很多噪音的情况，对于维度比较高噪音比较多的情况，lasso 可以在建模的同时做降维。

alphas = np.logspace(-4, 2, 100) # 尝试 100 个不同的 alpha

coeffs = np.zeros((len(alphas), X_train.shape[1]))
sse_train = np.zeros_like(alphas)
sse_test = np.zeros_like(alphas)

for n, alpha in enumerate(alphas):
    model = linear_model.Lasso(alpha=alpha)
    model.fit(X_train, y_train)
    coeffs[n, :] = model.coef_
    resid = y_train - model.predict(X_train)
    sse_train[n] = sum(resid**2)
    resid = y_test - model.predict(X_test)
    sse_test[n] = sum(resid**2)

fig, axes = plt.subplots(1, 2, figsize=(12, 4), sharex=True)

for n in range(coeffs.shape[1]):
    axes[0].plot(np.log10(alphas), coeffs[:, n], color=‘k‘, lw=0.5)

axes[1].semilogy(np.log10(alphas), sse_train, label="train")
axes[1].semilogy(np.log10(alphas), sse_test, label="test")
axes[1].legend(loc=0)

axes[0].set_xlabel(r"${\log_{10}}\alpha$", fontsize=18)
axes[0].set_ylabel(r"coefficients", fontsize=18)
axes[1].set_xlabel(r"${\log_{10}}\alpha$", fontsize=18)
axes[1].set_ylabel(r"sse", fontsize=18)
fig.tight_layout()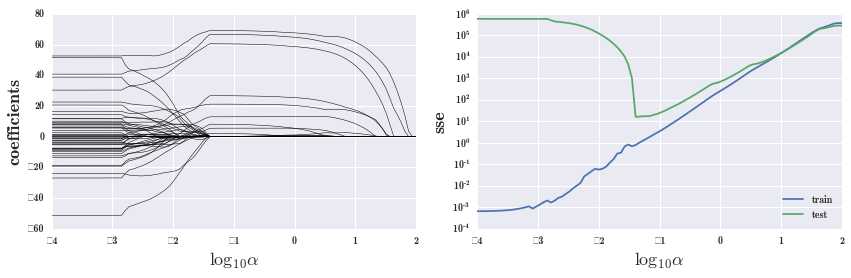

alpha 为 0 时，表示没有在 loss function 中放权重项，即没有惩罚，这时做回归，跟前面结果是一样的。

alpha 增大，很多噪音的因子就会降为 0，即对变量做筛选。

我们的目标是要使模型的预测效果最佳，自然要选择测试集上残差平方和最小的地方所对应的 alpha。

怎么求这个点，实际用时用 LassoCV 自动找出最好的 alpha。

model = linear_model.LassoCV() # 可以去尝试不同的参数值

model.fit(X_all, y_all)

LassoCV(alphas=None, copy_X=True, cv=None, eps=0.001, fit_intercept=True,
    max_iter=1000, n_alphas=100, n_jobs=1, normalize=False, positive=False,
    precompute=‘auto‘, random_state=None, selection=‘cyclic‘, tol=0.0001,
    verbose=False)

model.alpha_ # 自动找出最好的 alpha

0.06559238747534718

resid_train = y_train - model.predict(X_train)
sse_train = sse(resid_train)
print sse_train

1.76481994041

resid_test = y_test - model.predict(X_test)
sse_test = sse(resid_test)
print sse_test

1.31238073253

效果非常不错。

model.score(X_train, y_train), model.score(X_test, y_test)

(0.9999952185351132, 0.99999503689532787)

fig, ax = plot_residuals_and_coeff(resid_train, resid_test, model.coef_)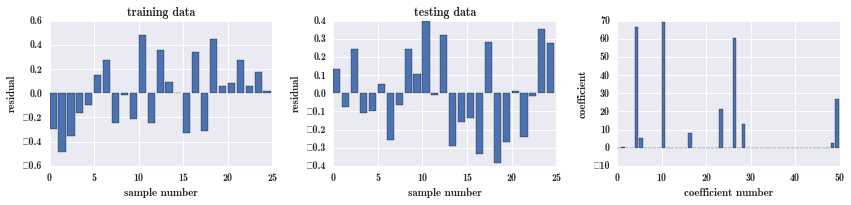

training 和 testing 的残差都比较小，无关变量的系数都被压到 0。效果非常好。

分类问题

分类问题和回归问题有什么区别？

分类的目标和回归不一样，虽然都是做预测，回归的 y 是连续的数值，分类预测的 y 是离散的数值，比如预测明天会不会下雨，就有会下雨和不会下雨两种情况，这是二元分类问题，编码时可编为 0 和 1 两种情况，还有是判断一个图形是什么阿拉伯数字，可能是 0,1,...,9，有 10 个可能的分类，是多元分类问题。

之前用的 statsmodels 的 logistic 回归就是分类模型，这里用 sklearn 中更多的分类模型。

sklearn 内有哪些分类模型？

• 广义线性模型

  • 岭回归
  • Logistic 回归
  • 贝叶斯回归

• 支持向量机

• 最近邻

• 朴素贝叶斯

• 决策树

iris = datasets.load_iris() # 载入鸢尾花数据集

print iris.target_names
print iris.feature_names

[‘setosa‘ ‘versicolor‘ ‘virginica‘]
[‘sepal length (cm)‘, ‘sepal width (cm)‘, ‘petal length (cm)‘, ‘petal width (cm)‘]

print iris.data.shape
print iris.target.shape

(150, 4)
(150,)

X_train, X_test, y_train, y_test = cross_validation.train_test_split(iris.data, iris.target, train_size=0.7) # 70% 用于训练，30% 用于检验

classifier = linear_model.LogisticRegression()
classifier.fit(X_train, y_train)

LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,
          intercept_scaling=1, max_iter=100, multi_class=‘ovr‘, n_jobs=1,
          penalty=‘l2‘, random_state=None, solver=‘liblinear‘, tol=0.0001,
          verbose=0, warm_start=False)

y_test_pred = classifier.predict(X_test)

如何评估分类效果？confusion matrix 是什么？

用 metrics 模块来检查模型效果，其中的 classification_report 是分类报告，显示各种指标，来衡量模型的效果。

print(metrics.classification_report(y_test, y_test_pred)) # 真实的 y 和预测的 y

             precision    recall  f1-score   support

          0       1.00      1.00      1.00        15
          1       1.00      0.75      0.86        16
          2       0.78      1.00      0.88        14

avg / total       0.93      0.91      0.91        45

precision 是精准度，recall 是召回率，fs-score 是 F1 值。从这几个值可以看到模型很完美。

还可以用混淆矩阵 confusion matrix 来评估分类器。混淆矩阵的每一列代表了预测类别，每一列的总数表示预测为该类别的数据的数目；每一行代表了数据的真实归属类别，每一行的数据总数表示该类别的数据实例的数目。每一列中的数值表示真实数据被预测为该类的数。如果混淆矩阵的所有数据都在对角线上，就说明预测是完全正确的。

metrics.confusion_matrix(y_test, y_test_pred)

array([[15,  0,  0],
       [ 0, 12,  4],
       [ 0,  0, 14]])

y_test.shape

(45,)

classifier = tree.DecisionTreeClassifier() # 决策树
classifier.fit(X_train, y_train)
y_test_pred = classifier.predict(X_test)
metrics.confusion_matrix(y_test, y_test_pred)

array([[12,  0,  0],
       [ 0, 13,  2],
       [ 0,  2, 16]])

classifier = neighbors.KNeighborsClassifier() # K 近邻
classifier.fit(X_train, y_train)
y_test_pred = classifier.predict(X_test)
metrics.confusion_matrix(y_test, y_test_pred)

array([[12,  0,  0],
       [ 0, 14,  1],
       [ 0,  2, 16]])

classifier = svm.SVC() # 支持向量机
classifier.fit(X_train, y_train)
y_test_pred = classifier.predict(X_test)
metrics.confusion_matrix(y_test, y_test_pred)

array([[12,  0,  0],
       [ 0, 15,  0],
       [ 0,  3, 15]])

classifier = ensemble.RandomForestClassifier()
classifier.fit(X_train, y_train)
y_test_pred = classifier.predict(X_test)
metrics.confusion_matrix(y_test, y_test_pred)

array([[12,  0,  0],
       [ 0, 14,  1],
       [ 0,  2, 16]])

train_size_vec = np.linspace(0.1, 0.9, 30) # 尝试不同的样本大小

classifiers = [tree.DecisionTreeClassifier,
               neighbors.KNeighborsClassifier,
               svm.SVC,
               ensemble.RandomForestClassifier
              ]

cm_diags = np.zeros((3, len(train_size_vec), len(classifiers)), dtype=float) # 用来放结果

for n, train_size in enumerate(train_size_vec):
    X_train, X_test, y_train, y_test =         cross_validation.train_test_split(iris.data, iris.target, train_size=train_size)

    for m, Classifier in enumerate(classifiers): 
        classifier = Classifier()
        classifier.fit(X_train, y_train)
        y_test_pred = classifier.predict(X_test)
        cm_diags[:, n, m] = metrics.confusion_matrix(y_test, y_test_pred).diagonal()
        cm_diags[:, n, m] /= np.bincount(y_test)

fig, axes = plt.subplots(1, len(classifiers), figsize=(12, 3))

for m, Classifier in enumerate(classifiers): 
    axes[m].plot(train_size_vec, cm_diags[2, :, m], label=iris.target_names[2])
    axes[m].plot(train_size_vec, cm_diags[1, :, m], label=iris.target_names[1])
    axes[m].plot(train_size_vec, cm_diags[0, :, m], label=iris.target_names[0])
    axes[m].set_title(type(Classifier()).__name__)
    axes[m].set_ylim(0, 1.1)
    axes[m].set_xlim(0.1, 0.9)
    axes[m].set_ylabel("classification accuracy")
    axes[m].set_xlabel("training size ratio")
    axes[m].legend(loc=4)

fig.tight_layout()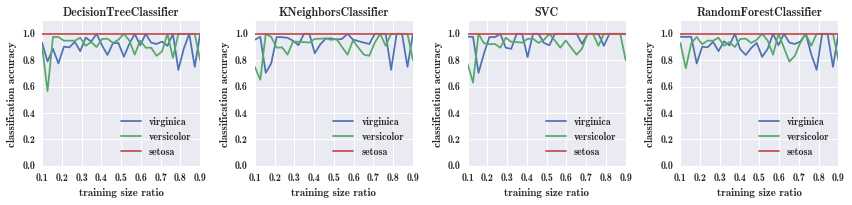

样本大小对预测分类结果有影响吗？

从上图可看出，当样本太小时，有些模型会表现很差，比如决策树、K 最近邻 和SVC，KNN 和 SVM 是比较依赖数据规模的。当 train size 变大后，分类准确率就比较高了。

聚类问题

聚类是一种无监督学习方法。

聚类问题的应用场景是什么？

主要解决把一群对象划分为若干个组的问题。例如用户细分：选择若干指标把用户群聚为若干个组，组内特征类似，组件特征差异明显。

应用最广泛的聚类方法是什么？

K-means 聚类。

X, y = iris.data, iris.target
np.random.seed(123)
n_clusters = 3 # 可以尝试其它值
c = cluster.KMeans(n_clusters=n_clusters) # 实例化
c.fit(X) # 这里的 fit 没有 y

KMeans(copy_x=True, init=‘k-means++‘, max_iter=300, n_clusters=3, n_init=10,
    n_jobs=1, precompute_distances=‘auto‘, random_state=None, tol=0.0001,
    verbose=0)

y_pred = c.predict(X)
print y_pred[::8]
print y[::8]

[1 1 1 1 1 1 1 2 2 2 2 2 2 0 0 0 0 0 0]
[0 0 0 0 0 0 0 1 1 1 1 1 1 2 2 2 2 2 2]

聚类结果是 1、2、0，真实结果是 0、1、2。为了跟真实值做比对，需要做个转换。

idx_0, idx_1, idx_2 = (np.where(y_pred == n) for n in range(3)) # 做转换
y_pred[idx_0], y_pred[idx_1], y_pred[idx_2] = 2, 0, 1
print y_pred[::8]
print y[::8]

[0 0 0 0 0 0 0 1 1 1 1 1 1 2 2 2 2 2 2]
[0 0 0 0 0 0 0 1 1 1 1 1 1 2 2 2 2 2 2]

print metrics.confusion_matrix(y, y_pred) # 当然在实际场景中是不可能有混淆矩阵的，因为根本就没有真实的 y

[[50  0  0]
 [ 0 48  2]
 [ 0 14 36]]

人大任务参考

标签：generator   which   sep   最小   pap   reg   例子   teacher   pos   

原文地址：http://www.cnblogs.com/zangrunqiang/p/6752402.html