标签:div 复杂度 ++ 运算 std 存在 利用 color lld
(一)通项公式
1 #include<cstdio> 2 #include<iostream> 3 #include<cmath> 4 5 using namespace std; 6 7 int main() 8 { 9 int n; 10 scanf("%d",&n); 11 n--; 12 double q=sqrt(5.0); 13 int ans; 14 ans=((pow((1+q)/2.0,n)/q-(pow((1-q)/2.0,n)/n))); 15 cout<<ans<<endl; 16 return 0; 17 }
(二)递归
递归是最慢的会发生重复计算,时间复杂度成指数级。
1 long long f(int n) 2 { 3 if(n==0) return 1; 4 else if(n==1) return 1; 5 //else if(n==2) return 2; 6 else return f(n-1)+f(n-2); 7 }
(三)循环
利用临时变量来保存中间的计算过程,能够加快运算。
1 long long f(int n) 2 { 3 long long a=1,b=2,c; 4 if(n==1) return 1; 5 else if(n==2)return 2; 6 else 7 { 8 for(int i=3; i<=n; i++) 9 { 10 c=a+b; 11 a=b; 12 b=c; 13 } 14 } 15 return b; 16 }
(四)矩阵乘法+空间换时间(减少乘法,取模运算)
数列的递推公式为:f(1)=1,f(2)=2,f(n)=f(n-1)+f(n-2)(n>=3)
用矩阵表示为:
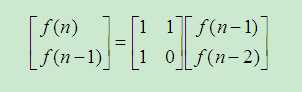
进一步,可以得出直接推导公式:
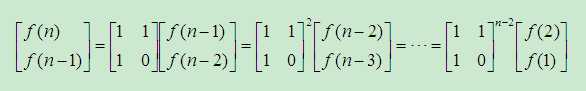
由于矩阵乘法满足结合律,在程序中可以事先给定矩阵的64,32,16,8,4,2,1次方,加快程序的执行时间。(有些题目需要取模运算,也可以事先进行一下)。给定的矩阵次幂,与二进制有关是因为,如下的公式存在解,满足Xi={0或1}:
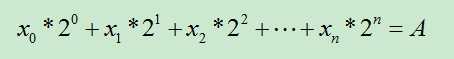
为了保证解满足 Xi={0或1},对上述公式的求解从右向左,即求解顺序为Xn,Xn-1,Xn-2,....,X1,X0。
完整代码实现如下:
1 /*求解f(n)%100000,其中n为大于等于3的正整数*/ 2 3 #include<cstdio> 4 #include<cmath> 5 6 long long f_tmp[6][4]= 7 { /*存放矩阵次幂*/ 8 /*位置:00 01 10 11*/ 9 {24578,78309,78309,46269}, //32次幂%100000 10 {1597,987,987,610}, //16次幂%100000 11 {34,21,21,13}, //8次幂%100000 12 {5,3,3,2}, //4次幂%100000 13 {2,1,1,1}, //2次幂%100000 14 {1,1,1,0}, //1次幂%100000 15 }; 16 17 void f(int k) 18 { //k>=3 19 int i; 20 long long t00=1,t01=1,t10=1,t11=0; //表示矩阵的1次幂 21 long long a,b,c,d; 22 k=k-3; //公式中是n-2次幂,(t00,t01,t10,t11)表示1次幂。所以一共减3次 23 for(i=k; i>=32; i=i-32) 24 { //对于大于等于32的k; 25 a=(t00*f_tmp[0][0]+t01*f_tmp[0][2])%100000; 26 b=(t00*f_tmp[0][1]+t01*f_tmp[0][3])%100000; 27 c=(t10*f_tmp[0][0]+t11*f_tmp[0][2])%100000; 28 d=(t10*f_tmp[0][1]+t11*f_tmp[0][3])%100000; 29 t00=a; 30 t01=b; 31 t10=c; 32 t11=d; 33 } 34 i=4; 35 while(i>=0) 36 { //对于小于32的k(16,8,4,2,1); 37 if(k>=(long long)pow(2,i)) 38 { //如果k大于某一个2的次幂 39 a=(t00*f_tmp[5-i][0]+t01*f_tmp[5-i][2])%100000; ///(5-i):矩阵的2的i次幂在数组fac_tmp中的位置为fac_tmp[5-i] 40 b=(t00*f_tmp[5-i][1]+t01*f_tmp[5-i][3])%100000; 41 c=(t10*f_tmp[5-i][0]+t11*f_tmp[5-i][2])%100000; 42 d=(t10*f_tmp[5-i][1]+t11*f_tmp[5-i][3])%100000; 43 t00=a; 44 t01=b; 45 t10=c; 46 t11=d; 47 k=k-(int)pow(2,i); 48 } 49 i--; 50 } 51 a=(t00*2+t01*1)%100000; 52 printf("%lld\n",a); 53 } 54 55 int main() 56 { 57 int n; 58 scanf("%d",&n); 59 f(n); 60 return 0; 61 }
标签:div 复杂度 ++ 运算 std 存在 利用 color lld
原文地址:http://www.cnblogs.com/zxqxwnngztxx/p/6772498.html