标签:规模 span code div com names next blog 树根
如题,给定一棵有根多叉树,请求出指定两个点直接最近的公共祖先。
输入格式:
第一行包含三个正整数N、M、S,分别表示树的结点个数、询问的个数和树根结点的序号。
接下来N-1行每行包含两个正整数x、y,表示x结点和y结点之间有一条直接连接的边(数据保证可以构成树)。
接下来M行每行包含两个正整数a、b,表示询问a结点和b结点的最近公共祖先。
输出格式:
输出包含M行,每行包含一个正整数,依次为每一个询问的结果。
5 5 4 3 1 2 4 5 1 1 4 2 4 3 2 3 5 1 2 4 5
4 4 1 4 4
时空限制:1000ms,128M
数据规模:
对于30%的数据:N<=10,M<=10
对于70%的数据:N<=10000,M<=10000
对于100%的数据:N<=500000,M<=500000
样例说明:
该树结构如下:
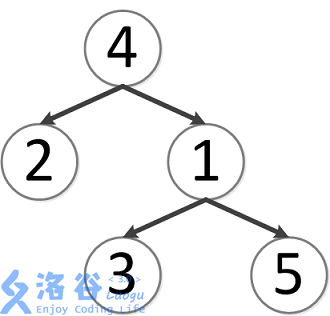
第一次询问:2、4的最近公共祖先,故为4。
第二次询问:3、2的最近公共祖先,故为4。
第三次询问:3、5的最近公共祖先,故为1。
第四次询问:1、2的最近公共祖先,故为4。
第五次询问:4、5的最近公共祖先,故为4。
故输出依次为4、4、1、4、4。
#include <bits/stdc++.h> #define N 500005 #define pb push_back using namespace std; vector<int>que[N]; struct node { int next,to; }edge[N<<2]; int head[N<<2],cnt,y,u[N],v[N],dad[N],n,m,root,fa[N],ans[N]; void add(int u,int v) { edge[++cnt].next=head[u]; edge[cnt].to=v; head[u]=cnt; } int read() { int x=0;char ch=getchar(); while(!isdigit(ch)) ch=getchar(); while(isdigit(ch)) { x=x*10+ch-‘0‘; ch=getchar(); } return x; } int find_(int x) {return x==fa[x]?x:fa[x]=find_(fa[x]);} void dfs(int x) { fa[x]=x; for(int i=head[x];i;i=edge[i].next) { int v=edge[i].to; if(dad[x]!=v) { dad[v]=x; dfs(v); } } for(int i=0;i<que[x].size();i++)if(dad[y=x^u[que[x][i]]^v[que[x][i]]]) ans[que[x][i]]=find_(y); fa[x]=dad[x]; } int main() { n=read(); m=read(); root=read(); int x,y; for(int i=1;i<n;i++) { x=read();y=read(); add(x,y); add(y,x); } for(int i=1;i<=m;i++) { u[i]=read();v[i]=read(); que[u[i]].pb(i); que[v[i]].pb(i); } dfs(root); for(int i=1;i<=m;i++) printf("%d\n",ans[i]); return 0; }
标签:规模 span code div com names next blog 树根
原文地址:http://www.cnblogs.com/ruojisun/p/6784820.html