标签:mic 分析 i++ limit 分享 sum cin 绝对值 cto
题目大意
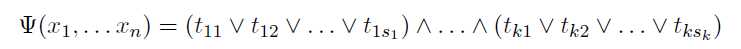
给出一个或与表达式,每个正变量和反变量最多出现一次,询问是否存在一种方案使得每个或式中有且仅有一个变量的值为1。
解题分析
将每个变量拆成三个点x,y,z。 y表示对应的正变量,z表示对应的反变量。
由S向每个点的x部连一条流量为1的边,表示该变量的某个正变量或反变量的取值为1。
由每个点的x部向y部和z部分别连一条流量为1的边,表示每个正变量和反变量仅有一个取值为1。
若某个或式中含有某个变量,则由该变量的y部或z部向或式连一条流量为1的边。表示该变量可以使该或式的结果为1。
由每个或式向T连一条流量为1的边,表示该或式被满足,且仅有一个变量的取值为1。
仅仅这么连还是不够的,因为如果某个变量的正变量和反变量同时出现,那么正变量或反变量中必定有一个值为1,对应到图上则是S向该变量的x部必须有1的流量。
所以可以向这条边添加上-1的费用,使得该变量的值优先被满足。
跑一遍最小费用最大流,如果是满流且费用的绝对值等于必须被确定值的变量的数量,则说明可以成功满足。
输出方案时只需遍历一下残余网络中的边,如果残余网络中没有流量则说明该变量被选择了,最后注意一下细节,确定一下对于每个变量选1还是选0。
参考程序

1 #include <bits/stdc++.h> 2 using namespace std; 3 4 #define rep(i,x,y) for (int i=x;i<=y;i++) 5 const int N=1000; 6 const int INF=2000000000; 7 8 int n,m,S,T,sum,minC,maxF; 9 int lt[N*4],flag[N],dis[N*4],pd[N*4],pre[N*4],sgn[N*4]; 10 vector <int> vec[N]; 11 12 struct edge{ 13 int u,v,f,w,nt; 14 }eg[N*6]; 15 16 void add(int u,int v,int f,int w) 17 { 18 //cout<<u<<" "<<v<<" "<<f<<" "<<w<<endl; 19 eg[++sum]=(edge){u,v,f,w,lt[u]}; lt[u]=sum; 20 eg[++sum]=(edge){v,u,0,-w,lt[v]}; lt[v]=sum; 21 } 22 23 bool spfa() 24 { 25 queue <int> Q; 26 rep (i,S,T) dis[i]=INF,pd[i]=0,pre[i]=-1; 27 dis[S]=0; pd[S]=1; Q.push(S); 28 while (!Q.empty()) 29 { 30 int u=Q.front(); 31 for (int i=lt[u];i;i=eg[i].nt) 32 { 33 int v=eg[i].v; 34 if (eg[i].f>0) 35 { 36 if (dis[u]+eg[i].w<dis[v]) 37 { 38 dis[v]=dis[u]+eg[i].w; 39 pre[v]=i; 40 if (!pd[v]) 41 { 42 Q.push(v); 43 pd[v]=1; 44 } 45 } 46 } 47 } 48 pd[u]=0; Q.pop(); 49 } 50 return dis[T]!=INF; 51 } 52 void minCmaxF() 53 { 54 int flow; 55 while (spfa()) 56 { 57 flow=INF; 58 for (int i=pre[T];~i;i=pre[eg[i].u]) 59 flow=min(flow,eg[i].f); 60 for (int i=pre[T];~i;i=pre[eg[i].u]) 61 eg[i].f-=flow,eg[i^1].f+=flow; 62 maxF+=flow; 63 minC+=flow*dis[T]; 64 } 65 } 66 67 int main() 68 { 69 freopen("sat.in","r",stdin); 70 freopen("sat.out","w",stdout); 71 72 cin.sync_with_stdio(0); 73 sum=1; memset(lt,0,sizeof(lt)); 74 int limit=0; 75 76 cin>>n>>m; 77 S=0; T=3*n+m+1; 78 rep(i,1,m) 79 { 80 int num; cin>>num; 81 rep(j,1,num) 82 { 83 int x; cin>>x; 84 flag[abs(x)]++; 85 if (x>0) sgn[x]=1; else sgn[x]=-1; 86 vec[i].push_back(x); 87 } 88 } 89 rep(i,1,n) if (flag[i]==2) add(S,i,1,-1),limit++; else add(S,i,1,0); 90 rep(i,1,n) {add(i,n+2*i-1,1,0); add(i,n+2*i,1,0);} 91 rep(i,1,m) 92 { 93 for (auto v:vec[i]) 94 { 95 int x=v>0?n+2*abs(v)-1:n+2*abs(v); 96 add(x,n*3+i,1,0); 97 } 98 add(3*n+i,T,1,0); 99 } 100 minC=maxF=0; 101 minCmaxF(); 102 vector <int> ans; 103 if (minC==-limit && maxF==m) 104 { 105 cout<<"YES"<<endl; 106 for (int i=lt[S];i;i=eg[i].nt) 107 { 108 if (eg[i].f==1) 109 { 110 if (sgn[eg[i].v]==1) ans.push_back(0); else ans.push_back(1); 111 } 112 else 113 { 114 if (eg[lt[eg[i].v]].f==0) ans.push_back(0); else ans.push_back(1); 115 } 116 } 117 for (int i=ans.size()-1;i>=0;i--) cout<<ans[i]<<" "; 118 cout<<endl; 119 } 120 else cout<<"NO"<<endl; 121 }

标签:mic 分析 i++ limit 分享 sum cin 绝对值 cto
原文地址:http://www.cnblogs.com/rpSebastian/p/6790809.html