标签:fine oid 代码 back efi 聚集 处理过程 const odi
vjudge 上题目链接:UVA 11235
*******************************************************大白书上解释************************************************************
题目大意:给出一个非降序排列的整数数组 a1,a2,a3,...,an,你的任务是对于一系列询问 (i, j),回答 ai,ai+1,...,aj 中出现次数最多的值所出现的次数。
输入格式:包含多组数据。每组数据第一行为两个整数 n 和 q(1 <= n, q <= 100000)。第二行包含 n 个非降序排列的整数 a1,a2,a3,...,an(-100000 <= ai <= 100000)。以下 q 行每行包含两个整数 i 和 j(1 <= i <= j <= n),输入结束标志为 n = 0。
输出格式:对于每个查询,输出查询结果。
分析:应注意到整个数组是非降序的,所有相等元素都会聚集到一起。这样就可以把整个数组进行游程编码(Run Length Encoding, RLE)。比如 -1,1,1,2,2,2,4 就可以编码成 (-1, 1), (1, 2), (2, 3), (4, 1),其中 (a, b) 表示有 b 个连续的 a。用 value[i] 和 count[i] 分别表示第 i 段的数值和出现次数,num[p], left[p], right[p] 分别表示位置 p 所在段的编号和左右端点位置,则在下图的情况,每次查询(L,R)的结果为以下 3 个部分的最大值:从 L 到 L 所在段的结束处的元素个数(即 right[L] - L + 1)、从 R 所在段的开始处到 R 处的元素个数(即 R - left[R] + 1)、中间第 num[L] + 1 段到第 num[R] - 1 段的 count 的最大值,如图 3-8 所示。
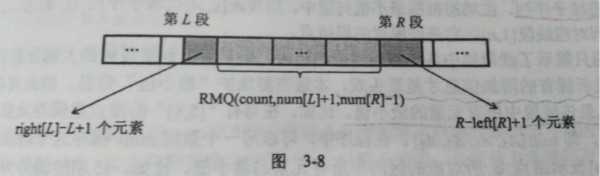
*******************************************************大白书上解释结束************************************************************
我的理解:
预处理过程主要就 3 个数组:seq[] 就是上述提到的 count[] 数组,记录 seq[i] 第 i 段连续整数的出现次数;pos[i] 表示原数组的第 i 个元素在 seq[] 中处于第几段;preSum[] 则是 seq 数组的前缀和,用于快速求出第 L 段和第 R 段的元素个数。这 3 个数组准备好后,接下来就是求区间最值的问题而已,线段树或者 RMQ 都可以,二者复杂度一样,时间差异可以忽略不计,只不过我更熟悉线段树,感觉 RMQ 的边界有点不容易处理而已。
首先是线段树的代码:
#include <cstdio> #include <cstring> #include <algorithm> #include <vector> #include <iostream> using namespace std; #define For(i,s,t) for(int i = (s); i < (t); ++i) #define root int rt, int l, int r #define ll(rt) ((rt) << 1) #define rr(rt) (ll(rt) | 1) #define makemid int mid = (l + r >> 1) #define lson ll(rt), l, mid #define rson rr(rt), mid + 1, r const int N = 100005; int c[N]; vector<int> seq, preSum; int pos[N] = {0,}; int Max[N << 2]; inline void pushup(int rt) { Max[rt] = max(Max[ll(rt)], Max[rr(rt)]); } void build(root) { if(l == r) { Max[rt] = seq[l - 1]; return; } makemid; build(lson); build(rson); pushup(rt); } int ql, qr; int query(root) { if(ql <= l && r <= qr) { return Max[rt]; } makemid; int ret = 0; if(ql <= mid) { ret = max(ret, query(lson)); } if(qr > mid) { ret = max(ret, query(rson)); } return ret; } int main() { int n,q; while(~scanf("%d",&n), n) { scanf("%d", &q); seq.clear(); scanf("%d", c); int curValue = c[0], curNum = 1; For(i, 1, n) { scanf("%d", c + i); if(c[i] == curValue) { ++curNum; pos[i] = pos[i - 1]; } else { seq.push_back(curNum); curValue = c[i]; curNum = 1; pos[i] = pos[i - 1] + 1; } } seq.push_back(curNum); preSum.clear(); preSum.push_back(seq[0]); int len = seq.size(); For(i, 1, len) { preSum.push_back(preSum[i - 1] + seq[i]); } build(1, 1, len); int x,y; while(q--) { scanf("%d %d",&x,&y); --x; --y; if(pos[x] == pos[y]) { printf("%d\n", y - x + 1); continue; } int lmax = preSum[pos[x]] - x; int rmax = y + 1 - preSum[pos[y] - 1]; int res = max(lmax, rmax); if(pos[y] == pos[x] + 1) { printf("%d\n", res); } else { ql = pos[x] + 1 + 1; qr = pos[y] - 1 + 1; printf("%d\n", max(res, query(1, 1, len))); } } } return 0; }
然后是 RMQ 的:
#include <cstdio> #include <cstring> #include <algorithm> #include <vector> #include <iostream> using namespace std; #define For(i,s,t) for(int i = (s); i < (t); ++i) const int N = 100005; int c[N]; vector<int> seq, preSum; int pos[N] = {0,}; int d[N][18]; inline void init(int n) { For(i, 0, n) { d[i][0] = seq[i]; } for(int j = 1; (1 << j) < n; ++j) { for(int i = 0; i + (1 << j) - 1 < n; ++i) { d[i][j] = max(d[i][j - 1], d[i + (1 << (j - 1))][j - 1]); } } } inline int rmq(int L, int R) { int k = 0, len = R - L + 1; while((1 << (k + 1)) < len) ++k; return max(d[L][k], d[R - (1 << k) + 1][k]); } int main() { int n,q; while(~scanf("%d",&n), n) { scanf("%d", &q); seq.clear(); scanf("%d", c); int curValue = c[0], curNum = 1; For(i, 1, n) { scanf("%d", c + i); if(c[i] == curValue) { ++curNum; pos[i] = pos[i - 1]; } else { seq.push_back(curNum); curValue = c[i]; curNum = 1; pos[i] = pos[i - 1] + 1; } } seq.push_back(curNum); preSum.clear(); preSum.push_back(seq[0]); int len = seq.size(); For(i, 1, len) { preSum.push_back(preSum[i - 1] + seq[i]); } init(len); int x,y; while(q--) { scanf("%d %d",&x,&y); --x; --y; if(pos[x] == pos[y]) { printf("%d\n", y - x + 1); continue; } int lmax = preSum[pos[x]] - x; int rmax = y + 1 - preSum[pos[y] - 1]; int res = max(lmax, rmax); if(pos[y] == pos[x] + 1) { printf("%d\n", res); } else { int ql = pos[x] + 1; int qr = pos[y] - 1; printf("%d\n", max(res, rmq(ql, qr))); } } } return 0; }
UVA 11235 Frequent values 线段树/RMQ
标签:fine oid 代码 back efi 聚集 处理过程 const odi
原文地址:http://www.cnblogs.com/Newdawn/p/6818204.html