机器学习笔记（Washington University）- Regression Specialization-week five

标签：end   atoi   form   lua   less   when   ror   sel   ice   

1. Feature selection

Sometimes, we need to decrease the number of features

Efficiency:

With fewer features, we can compute quickly

Interpretaility:

what relevant features are for the preidction task

2.  All subsets algorithm

We just take every possible combination of features we want to include in our model.

and we can evaluate them using the validation set or the cross validatoin. But the complexity is

that if the number of features D is large, then the choices goes up to O(2^D)

3. Greedy algorithm

We fit model using the current feature set(or empty), then we start to select the next best feature

with the lowest trainning error. And the complexity has been reduced to O(D^2)

4. Lasso

For ridge, the weights have been shrunk, but it is reduced to zero. Now we want to get some coefficients

exactly to zero. Firstly we cannot just set small ridge coefficients to zero, because the correalted features will

all get small weights, maybe it is relevant to our predictions.lasso add the bias to reduce variance, and with

group of highly correlated features, lasso tends to select arbitrarily.

Lasso regression(L1 regularized regression)

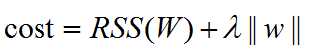
lambda s used to balance fit of the model and sparsity.

when lambda is between 0 and infinity， the solution of W(Lasso) is between 0 and W(Least square solution)

The gradient of |w| does not exist when Wj = 0, And there is no close-form solution for lasso. 

and we can use subgradients instead of using gradients

5. Coordinate descent

At each iteration, we only update only one coordinate instead of all coordinates, so we get this axis-aligned moves.

And we do not need to choose stepsize.

6. Normalize Features

We need to normalize both the training set and test set.

7. Coordinate descent for least squares regression

Suppose the feature is normalized and we get the partial deriative:

while not converged:
　　for j =[0,1,2...D]
　　　　compute ρj
　　　　and set wj=ρj

and in the case case of lasso, lambda is our tuning parameter for the model

while not converged:
　　for j =[0,1,2...D]
　　　　compute ρj
　　　　and set wj= ρj+λ/2(if ρj<-λ/2), 0(if ρj in [λ/2,λ/2]]),ρj=λ/2(if ρj>-λ/2)

in coordinate descent, the convergence is detected when over an entire sweep of all coordinates, if the

maximum step you take is less than your tolerance.

机器学习笔记（Washington University）- Regression Specialization-week five

标签：end   atoi   form   lua   less   when   ror   sel   ice   

原文地址：http://www.cnblogs.com/climberclimb/p/6819709.html