标签：过拟合   顺序   信息论   优化   测试   遍历   策略   字段   应用   

　　机器学习按数据的使用方式来说可以分为有监督学习、无监督学习、半监督学习、强化学习等，机器学习中的算法还有另外一种划分方式：分类、聚类、回归。但我更喜欢分为两种：广义的分类（分类+聚类）和回归，这里是按照预测的结果是离散数据还是连续数据来划分的。今天要介绍的决策树就是分类算法中的一种。

　　在介绍机器学习和深度学习方法时，笔者将按照以下顺序来介绍相关理论：1.主要概念的定义 2.模型工作原理 3.最优化策略 4.模型训练方法 5.优缺点评估 6.应用（在第二篇介绍）

　　1主要概念

　　决策树：决策树是一种树形结构，其中每个内部节点表示一个实例在一个属性上的测试，每个分支代表一个实例测试输出的结果，每个叶节点代表一种类别。

　　剪枝：将决策树的一颗树的子节点全部删掉，根节点作为叶子结点，其目的在于避免过拟合。

　　信息熵：由信息论之父香浓提出，表示信息的不确定性，计算公式为

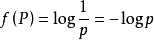
在这里，P指的是实例属于某种类别的概率，n是类别的总数。这个公式所蕴含的意思就是分类越多，信息熵越大，这里信息熵的值本身是没有任何意义的，其存在的意义在于有一个可以比较的尺度，当需要比较两个信息谁更混乱时，这里信息熵才有了用武之地！

　　2决策树的工作原理

　　对于一个训练好的决策树来说，当有一个新数据需要预测其分类时，首先以根节点的属性查找实例对应的值，然后决策应该选择哪个分支，在选定分支后按照下一个节点对应的属性继续查找实例对应属性的值，然后决策此节点应该选的分支，依次类推，得到叶子结点，叶子结点所对应的类别就是决策树预测的实例所属分类。

3决策树的最优化策略

　　在构建决策树的过程中，当我们需要选取某个属性作为分支的判断条件时，我们需要知道在众多的属性中应该选择哪一个最好。这时，我们需要有一个可以衡量的指标，根据这个指标来选择属性。决策树模型有比较多的指标可供我们选择，这里介绍3种。

3.1信息增益（ID3算法）

　　信息增益是ID3算法所使用的最优化策略，在这里就用到了信息熵的概念。 当我们为某个节点选择属性时，首先衡量选择属性之前的信息熵H，然后遍历所有属性，分别求选择对应属性后的信息熵Hi，这时，信息增益可以表示为Gain(A)=H-Hi，A表示所选的属性。

3.2信息增益率(C4.5算法)

　　使用信息增益选择属性时，这种方法往往倾向于选择属性值较多的属性。举个极端的例子，所有实例在属性A上的属性值都不重复，那么在使用这个属性决策时如果将每个数据自成一个分支，那么直接得到分类结果，此时信息熵为直接变为0，信息增益最大，但显然这种方法是不合理的，至少会发生过拟合。这里可以引入一个惩罚因子，那么可以认为信息增益率=惩罚参数*信息增益，这里

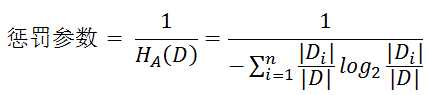
其中D代表数据集，Di代表数据集按照值的划分，相同的值的数据在同一个划分中，否则不在。信息增益率的缺点与信息增益恰恰相反，这种方法倾向于选择取值较少的特征。。。

基于以上缺点，并不是直接选择信息增益率最大的特征，而是现在候选特征中找出信息增益高于平均水平的特征，然后在这些特征中再选择信息增益率最高的特征。

3.3基尼指数(CART算法)

　　定义：基尼指数（基尼不纯度）：表示在样本集合中一个随机选中的样本被分错的概率。

Gini指数越小表示集合中被选中的样本被分错的概率越小，也就是说集合的纯度越高，反之，集合越不纯。

即 基尼指数（基尼不纯度）= 样本被选中的概率 * 样本被分错的概率。用公式表示：

4决策树的训练

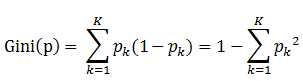
决策树构建的基本步骤如下：

1. 开始，所有记录看作一个节点

2. 遍历每个变量（属性）的每一种分割方式，找到最好的分割点

3. 分割成两个节点N₁和N₂

4. 对N₁和N₂分别继续执行2-3步，直到每个节点足够“纯”或者没有变量（属性）可以划分节点为止

5决策树的优缺点

优点：

　　1速度快，计算量相对较小，比较容易转化成规则

　　2便于理解，可以很清晰的显示出哪些属性比较重要

缺点：

　　1缺乏伸缩性，由于进行深度优先搜索，所以非常吃内存，难于处理大数据集

　　2连续型字段难于处理

　　3当类别太多时，错误可能会增加的比较快

决策树系列（一）决策树基础

标签：过拟合   顺序   信息论   优化   测试   遍历   策略   字段   应用   

原文地址：http://www.cnblogs.com/xueyinzhe/p/6820891.html