标签:通知 shift abs pointer state 数据结构 冲突 equals unpark
为什么把这两个数据结构对比分析呢,相信大家都明白。首先二者都是线程安全的,但是二者保证线程安全的方式却是不同的。废话不多说了,从源码的角度分析一下两者的异同,首先给出二者的继承关系图。
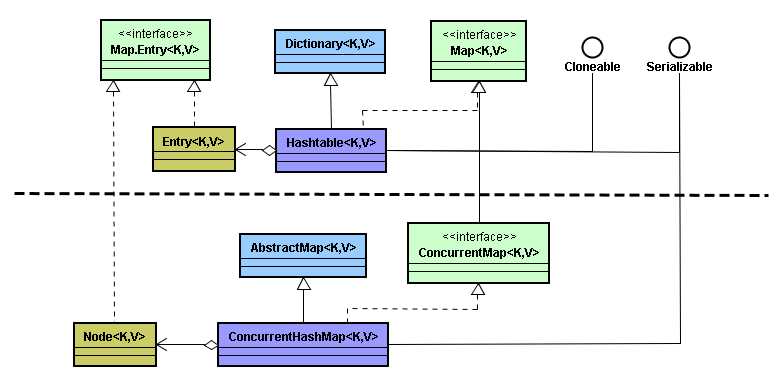
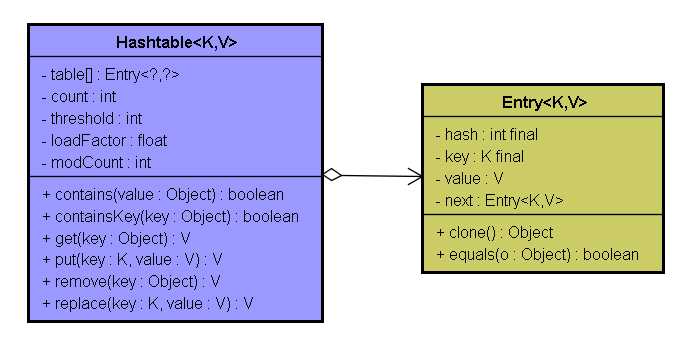
我们还是先给出一张Hashtable类的属性和方法图,其中Entry<K,V>是Hashtable类的静态内部类,该类继承自Map.Entry<K,V>接口。如下将会详细讲解Hashtable类中属性和方法的含义。

public static void main(String[] args) { Hashtable<Integer, String> tb = new Hashtable<Integer,String>(); tb.put(1, "BUPT"); tb.put(2, "PKU"); tb.put(3, "THU"); Iterator<Entry<Integer, String>> iter = tb.entrySet().iterator(); while(iter.hasNext()){ Entry<?, ?> entry = (Entry<?, ?>) iter.next(); //此处会抛出异常 System.out.println(entry.getValue()); if("THU".equals(entry.getValue())){ tb.remove(entry.getKey()); } } } /* 输出结果如下: THU Exception in thread "main" java.util.ConcurrentModificationException at java.util.Hashtable$Enumerator.next(Hashtable.java:1367) at ali.Main.main(Main.java:16) */
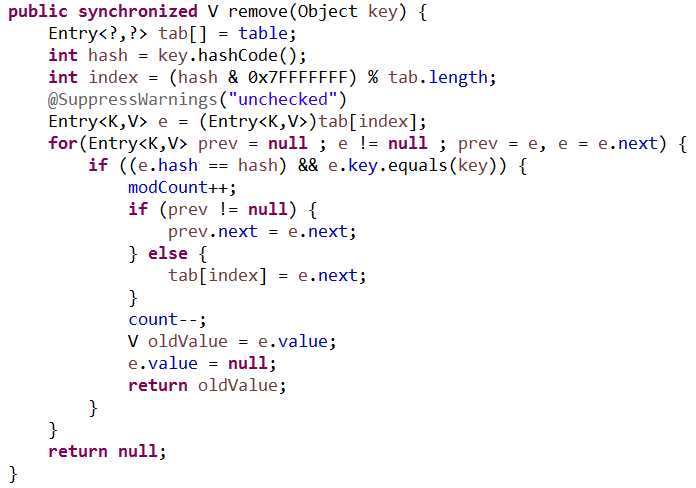
Hashtable的remove(Object key)方法见如下方法5,每一次修改hashtable中的数据都更新modCount的值。Hashtable内部类Enumerator<T>的相关部分代码如下:

private class Enumerator<T> implements Enumeration<T>, Iterator<T> { Entry<?,?>[] table = Hashtable.this.table; int index = table.length; Entry<?,?> entry; Entry<?,?> lastReturned; int type; /** * Indicates whether this Enumerator is serving as an Iterator * or an Enumeration. (true -> Iterator). */ boolean iterator; /** * 遍历之初将hashtable修改的次数赋值给expectedModCount */ protected int expectedModCount = modCount; Enumerator(int type, boolean iterator) { this.type = type; this.iterator = iterator; } // public boolean hasMoreElements() { Entry<?,?> e = entry; int i = index; Entry<?,?>[] t = table; /* Use locals for faster loop iteration */ while (e == null && i > 0) { e = t[--i]; } entry = e; index = i; return e != null; } @SuppressWarnings("unchecked") public T nextElement() { Entry<?,?> et = entry; int i = index; Entry<?,?>[] t = table; /* Use locals for faster loop iteration */ while (et == null && i > 0) { et = t[--i]; } entry = et; index = i; if (et != null) { Entry<?,?> e = lastReturned = entry; entry = e.next; return type == KEYS ? (T)e.key : (type == VALUES ? (T)e.value : (T)e); } throw new NoSuchElementException("Hashtable Enumerator"); } //查看是否还有下一个元素 public boolean hasNext() { return hasMoreElements(); } public T next() { //首先判断modCount和expectedModCount是否相等 //由于在主程序中Hashtable对象通过tb.remove()方法修改了modCount的值,使得expectedModCount和modCount不相等而抛出异常 //解决办法就是将tb.remove()方法替换为iter.remove()方法 if (modCount != expectedModCount) throw new ConcurrentModificationException(); return nextElement(); } //该方法在remove元素的同时修改了modCount和expectedModCount的值 public void remove() { if (!iterator) throw new UnsupportedOperationException(); if (lastReturned == null) throw new IllegalStateException("Hashtable Enumerator"); if (modCount != expectedModCount) throw new ConcurrentModificationException(); synchronized(Hashtable.this) { Entry<?,?>[] tab = Hashtable.this.table; int index = (lastReturned.hash & 0x7FFFFFFF) % tab.length; @SuppressWarnings("unchecked") Entry<K,V> e = (Entry<K,V>)tab[index]; for(Entry<K,V> prev = null; e != null; prev = e, e = e.next) { if (e == lastReturned) { modCount++; expectedModCount++; if (prev == null) tab[index] = e.next; else prev.next = e.next; count--; lastReturned = null; return; } } throw new ConcurrentModificationException(); } } }

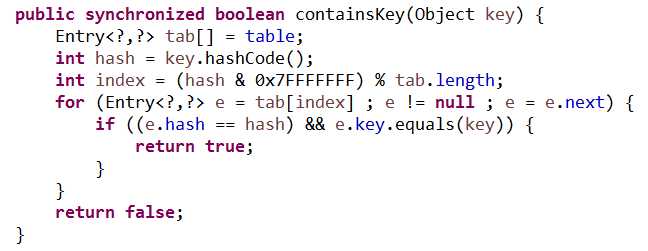
get(Object key),获取当前键key所对应的value值,本方法和containsKey(Object key)方法除了返回值其它都相同,如果能找到该key对应的value,则返回value的值,如果不能则返回false。
put(K key, V value),将该键值对加入table中。首先插入的value不能为空。其次如果当前插入的key值已经在table中存在,则用新的value替换掉原来的value值,并将原来的value值作为该方法的返回值返回。如果当前插入的key不在table中,则将该键值对插入。
插入的方法首先判断当前table中的值是否大于阈值(threshold),如果大于该阈值,首先对该表扩容,再将新的键值对插入table[index]的链表的第一个Entry的位置上。
replace(K key, V value),将键为key的Entry对象值更新为value,并将原来的value最为该方法的返回值。
ConcurrentHashMap在JDK1.8中改动还是挺大的。它摒弃了Segment(段锁)的概念,在实现上采用了CAS算法。底层使用数组+链表+红黑树的方式,但是为了做到并发,同时也增加了大量的辅助类。如下是ConcurrentHashMap的类图。
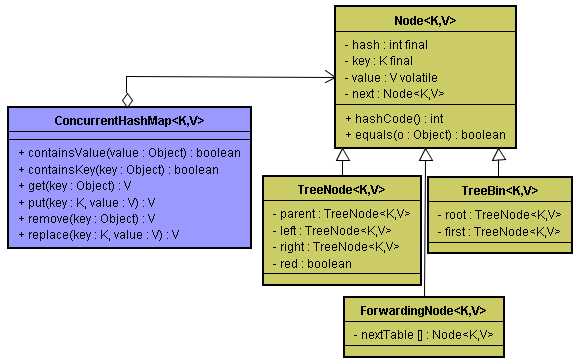
//ConcurrentHashMap最大容量 private static final int MAXIMUM_CAPACITY = 1 << 30; //ConcurrentHashMap初始默认容量 private static final int DEFAULT_CAPACITY = 16; //最大table数组的大小 static final int MAX_ARRAY_SIZE = Integer.MAX_VALUE - 8; //默认并行级别,主体代码并未使用 private static final int DEFAULT_CONCURRENCY_LEVEL = 16; //加载因子,默认为0.75 private static final float LOAD_FACTOR = 0.75f; //当hash桶中hash冲突的数目大于此值时,将链表转化为红黑树,加快hash的查找速度 static final int TREEIFY_THRESHOLD = 8; //当hash桶中hash冲突小于等于此值时,会把红黑树转化为链表 static final int UNTREEIFY_THRESHOLD = 6; //当table数组的长度大于该值时,同时满足hash桶中hash冲突大于TREEIFY_THRESHOLD时,才会把链表转化为红黑树 static final int MIN_TREEIFY_CAPACITY = 64; //扩容操作中,transfer()方法允许多线程,该值表示一个线程执行transfer时,至少对连续的多少个hash桶进行transfer private static final int MIN_TRANSFER_STRIDE = 16; //ForwardingNode的hash值,ForwardingNode是一种临时节点,在扩容中才会出现,不存储实际的数据 static final int MOVED = -1; //TreeBin的hash值,TreeBin是用于代理TreeNode的特殊节点,存储红黑树的根节点 static final int TREEBIN = -2; //用于和负数hash进行&运算,将其转化为正数 static final int HASH_BITS = 0x7fffffff;

static class Node<K,V> implements Map.Entry<K,V> { final int hash; final K key; volatile V val; volatile Node<K,V> next; Node(int hash, K key, V val, Node<K,V> next) { this.hash = hash; this.key = key; this.val = val; this.next = next; } public final K getKey() { return key; } public final V getValue() { return val; } public final int hashCode() { return key.hashCode() ^ val.hashCode(); } public final String toString(){ return key + "=" + val; } //不支持直接设置value的值 public final V setValue(V value) { throw new UnsupportedOperationException(); } public final boolean equals(Object o) { Object k, v, u; Map.Entry<?,?> e; return ((o instanceof Map.Entry) && (k = (e = (Map.Entry<?,?>)o).getKey()) != null && (v = e.getValue()) != null && (k == key || k.equals(key)) && (v == (u = val) || v.equals(u))); } //从当前节点查找对应的键为k的Node<K,V> Node<K,V> find(int h, Object k) { Node<K,V> e = this; if (k != null) { do { K ek; if (e.hash == h && ((ek = e.key) == k || (ek != null && k.equals(ek)))) return e; } while ((e = e.next) != null); } return null; } }

static final class TreeNode<K,V> extends Node<K,V> { TreeNode<K,V> parent; // red-black tree links TreeNode<K,V> left; TreeNode<K,V> right; //当前节点的前一个结点,从而方便删除 TreeNode<K,V> prev; // needed to unlink next upon deletion boolean red; TreeNode(int hash, K key, V val, Node<K,V> next, TreeNode<K,V> parent) { super(hash, key, val, next); this.parent = parent; } Node<K,V> find(int h, Object k) { return findTreeNode(h, k, null); } //查找hashcode为h,key为k的TreeNode结点 final TreeNode<K,V> findTreeNode(int h, Object k, Class<?> kc) { if (k != null) { TreeNode<K,V> p = this; do { int ph, dir; K pk; TreeNode<K,V> q; TreeNode<K,V> pl = p.left, pr = p.right; if ((ph = p.hash) > h) p = pl; else if (ph < h) p = pr; else if ((pk = p.key) == k || (pk != null && k.equals(pk))) return p; else if (pl == null) p = pr; else if (pr == null) p = pl; else if ((kc != null || (kc = comparableClassFor(k)) != null) && (dir = compareComparables(kc, k, pk)) != 0) p = (dir < 0) ? pl : pr; else if ((q = pr.findTreeNode(h, k, kc)) != null) return q; else p = pl; } while (p != null); } return null; } }

static final class ForwardingNode<K,V> extends Node<K,V> { final Node<K,V>[] nextTable; //构造函数指定hash值为MOVED,key=null, value=null, next=null ForwardingNode(Node<K,V>[] tab) { super(MOVED, null, null, null); this.nextTable = tab; } Node<K,V> find(int h, Object k) { //for循环避免多次遇见ForwardingNode导致递归过深 outer: for (Node<K,V>[] tab = nextTable;;) { Node<K,V> e; int n; if (k == null || tab == null || (n = tab.length) == 0 || (e = tabAt(tab, (n - 1) & h)) == null) return null; for (;;) { int eh; K ek; if ((eh = e.hash) == h && ((ek = e.key) == k || (ek != null && k.equals(ek)))) return e; if (eh < 0) { //如果遇见ForwardingNode结点,则遍历ForwardingNode的nextTable结点 if (e instanceof ForwardingNode) { tab = ((ForwardingNode<K,V>)e).nextTable; continue outer; } else return e.find(h, k); } if ((e = e.next) == null) return null; } } } }
补充图一张说明扩容下是如何遍历结点的。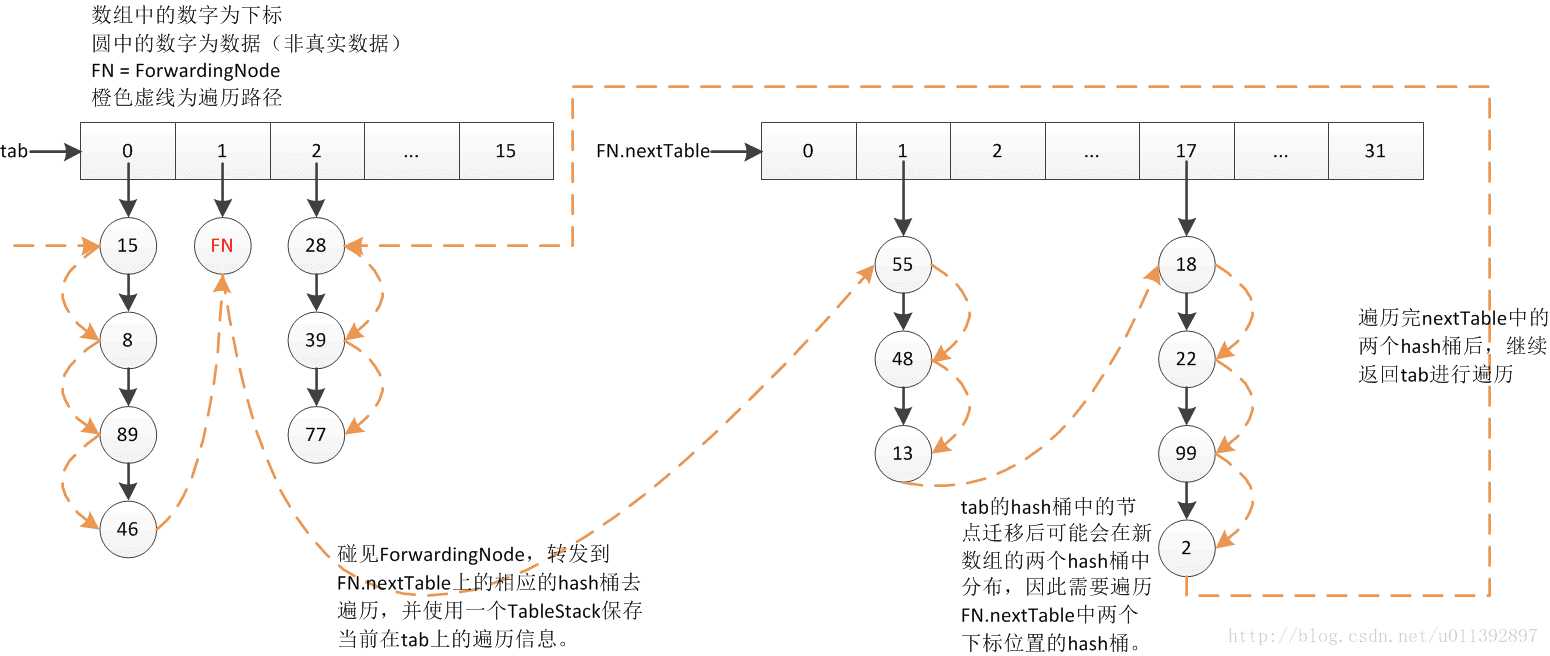

static final class TreeBin<K,V> extends Node<K,V> { TreeNode<K,V> root; //红黑树的根节点 volatile TreeNode<K,V> first; //链表的头结点 volatile Thread waiter; //最近一个设置waiter标志位的线程 volatile int lockState; //全局的锁状态 // values for lockState static final int WRITER = 1; // set while holding write lock 写锁状态 static final int WAITER = 2; // set when waiting for write lock 等待获取写锁的状态 static final int READER = 4; // increment value for setting read lock 读锁状态,读锁可以叠加,即红黑树可以并发读,每增加一个读线程lockState的值加READER /** * 红黑树的读锁状态和写锁状态是互斥的,但是读写操作实际上可以是不互斥的 * 红黑树的读写状态互斥是指以红黑树的方式进行读写操作时互斥的 * 当线程持有红黑树的写锁时,读线程不能以红黑树的方式进行读取操作,但可以用简单链表的方式读取,从而实现了读写操作的并发执行 * 当有线程持有红黑树的读锁时,写线程会阻塞,但是红黑树查找速度快,因此写线程阻塞时间短。 * put/remove/replace方法会锁住TreeBin节点,因此不会出现写-写竞争。 */ //当hashCode相等且不是Comparable类时使用此方法判断大小 static int tieBreakOrder(Object a, Object b) { int d; if (a == null || b == null || (d = a.getClass().getName(). compareTo(b.getClass().getName())) == 0) d = (System.identityHashCode(a) <= System.identityHashCode(b) ? -1 : 1); return d; } //以b为头节点的链表创建红黑树 TreeBin(TreeNode<K,V> b) { super(TREEBIN, null, null, null); this.first = b; TreeNode<K,V> r = null; for (TreeNode<K,V> x = b, next; x != null; x = next) { next = (TreeNode<K,V>)x.next; x.left = x.right = null; if (r == null) { x.parent = null; x.red = false; r = x; } else { K k = x.key; int h = x.hash; Class<?> kc = null; for (TreeNode<K,V> p = r;;) { int dir, ph; K pk = p.key; if ((ph = p.hash) > h) dir = -1; else if (ph < h) dir = 1; else if ((kc == null && (kc = comparableClassFor(k)) == null) || (dir = compareComparables(kc, k, pk)) == 0) dir = tieBreakOrder(k, pk); TreeNode<K,V> xp = p; if ((p = (dir <= 0) ? p.left : p.right) == null) { x.parent = xp; if (dir <= 0) xp.left = x; else xp.right = x; r = balanceInsertion(r, x); break; } } } } this.root = r; assert checkInvariants(root); } /** * 红黑树重构时西药对根节点加写锁 */ private final void lockRoot() { //尝试获取一次锁 if (!U.compareAndSwapInt(this, LOCKSTATE, 0, WRITER)) contendedLock(); //直到获取到写锁,该方法才返回 } /** * 释放写锁 */ private final void unlockRoot() { lockState = 0; } /** * 阻塞写线程,当写线程获取写锁时返回 *因为ConcurrentHashMap的put/remove/replace方法会对TreeBin加锁,因此不会出现写-写竞争 *因此该方法只用考虑读锁线程阻碍线程获取写锁,而不用考虑写锁线程阻碍线程获取写锁,不用考虑写-写竞争 */ private final void contendedLock() { boolean waiting = false; for (int s;;) { //~WAITER表示反转WAITER,当没哟线程持有读锁时,该条件为true if (((s = lockState) & ~WAITER) == 0) { if (U.compareAndSwapInt(this, LOCKSTATE, s, WRITER)) { //没有任何线程持有读写锁时,尝试让当前线程获取写锁,同时清空waiter标识位 if (waiting) waiter = null; return; } } else if ((s & WAITER) == 0) { //当前线程持有读锁,并且当前线程不是WAITER状态时,该条件为true if (U.compareAndSwapInt(this, LOCKSTATE, s, s | WAITER)) { //尝试占据WAITER标识位 waiting = true; //表明自己处于waiter状态 waiter = Thread.currentThread(); } } else if (waiting) //当前线程持有读锁,并且当前线程处于waiter状态时,该条件为true LockSupport.park(this); //阻塞自己 } } /** * 从根节点开始查找,找不到返回null * 当有写线程加上写锁时,使用链表方式进行查找 */ final Node<K,V> find(int h, Object k) { if (k != null) { for (Node<K,V> e = first; e != null; ) { int s; K ek; //两种特殊情况下以链表的方式进行查找 //1、有线程正持有 写锁,这样做能够不阻塞读线程 //2、WAITER时,不再继续加 读锁,能够让已经被阻塞的写线程尽快恢复运行,或者刚好让某个写线程不被阻塞 if (((s = lockState) & (WAITER|WRITER)) != 0) { if (e.hash == h && ((ek = e.key) == k || (ek != null && k.equals(ek)))) return e; e = e.next; } // 读线程数量加1,读状态进行累加 else if (U.compareAndSwapInt(this, LOCKSTATE, s, s + READER)) { TreeNode<K,V> r, p; try { p = ((r = root) == null ? null : r.findTreeNode(h, k, null)); } finally { Thread w; // 如果这是最后一个读线程,并且有写线程因为 读锁 而阻塞,那么要通知它,告诉它可以尝试获取写锁了 if (U.getAndAddInt(this, LOCKSTATE, -READER) == (READER|WAITER) && (w = waiter) != null) LockSupport.unpark(w); // 让被阻塞的写线程运行起来,重新去尝试获取写锁 } return p; } } } return null; } /** *在ConcurrentHashMap的putVal方法如果hash桶为红黑树时调用 */ final TreeNode<K,V> putTreeVal(int h, K k, V v) { Class<?> kc = null; boolean searched = false; for (TreeNode<K,V> p = root;;) { int dir, ph; K pk; if (p == null) { first = root = new TreeNode<K,V>(h, k, v, null, null); break; } else if ((ph = p.hash) > h) dir = -1; else if (ph < h) dir = 1; else if ((pk = p.key) == k || (pk != null && k.equals(pk))) return p; else if ((kc == null && (kc = comparableClassFor(k)) == null) || (dir = compareComparables(kc, k, pk)) == 0) { if (!searched) { TreeNode<K,V> q, ch; searched = true; if (((ch = p.left) != null && (q = ch.findTreeNode(h, k, kc)) != null) || ((ch = p.right) != null && (q = ch.findTreeNode(h, k, kc)) != null)) return q; } dir = tieBreakOrder(k, pk); } TreeNode<K,V> xp = p; if ((p = (dir <= 0) ? p.left : p.right) == null) { TreeNode<K,V> x, f = first; first = x = new TreeNode<K,V>(h, k, v, f, xp); if (f != null) f.prev = x; if (dir <= 0) xp.left = x; else xp.right = x; if (!xp.red) x.red = true; else { lockRoot(); try { root = balanceInsertion(root, x); } finally { unlockRoot(); } } break; } } assert checkInvariants(root); return null; } /** * 从链表和红黑树上都删除结点 * 两点区别:1、返回值,红黑树的规模太小时,返回true,调用者再去进行树->链表的转化; * 2、红黑树规模足够,不用变换成链表时,进行红黑树上的删除要加 写锁 */ final boolean removeTreeNode(TreeNode<K,V> p) { TreeNode<K,V> next = (TreeNode<K,V>)p.next; TreeNode<K,V> pred = p.prev; // unlink traversal pointers TreeNode<K,V> r, rl; if (pred == null) first = next; else pred.next = next; if (next != null) next.prev = pred; if (first == null) { root = null; return true; } if ((r = root) == null || r.right == null || // too small (rl = r.left) == null || rl.left == null) return true; lockRoot(); try { TreeNode<K,V> replacement; TreeNode<K,V> pl = p.left; TreeNode<K,V> pr = p.right; if (pl != null && pr != null) { TreeNode<K,V> s = pr, sl; while ((sl = s.left) != null) // find successor s = sl; boolean c = s.red; s.red = p.red; p.red = c; // swap colors TreeNode<K,V> sr = s.right; TreeNode<K,V> pp = p.parent; if (s == pr) { // p was s‘s direct parent p.parent = s; s.right = p; } else { TreeNode<K,V> sp = s.parent; if ((p.parent = sp) != null) { if (s == sp.left) sp.left = p; else sp.right = p; } if ((s.right = pr) != null) pr.parent = s; } p.left = null; if ((p.right = sr) != null) sr.parent = p; if ((s.left = pl) != null) pl.parent = s; if ((s.parent = pp) == null) r = s; else if (p == pp.left) pp.left = s; else pp.right = s; if (sr != null) replacement = sr; else replacement = p; } else if (pl != null) replacement = pl; else if (pr != null) replacement = pr; else replacement = p; if (replacement != p) { TreeNode<K,V> pp = replacement.parent = p.parent; if (pp == null) r = replacement; else if (p == pp.left) pp.left = replacement; else pp.right = replacement; p.left = p.right = p.parent = null; } root = (p.red) ? r : balanceDeletion(r, replacement); if (p == replacement) { // detach pointers TreeNode<K,V> pp; if ((pp = p.parent) != null) { if (p == pp.left) pp.left = null; else if (p == pp.right) pp.right = null; p.parent = null; } } } finally { unlockRoot(); } assert checkInvariants(root); return false; } /* ------------------------------------------------------------ */ // 如下是红黑树的经典算法 static <K,V> TreeNode<K,V> rotateLeft(TreeNode<K,V> root, TreeNode<K,V> p) { TreeNode<K,V> r, pp, rl; if (p != null && (r = p.right) != null) { if ((rl = p.right = r.left) != null) rl.parent = p; if ((pp = r.parent = p.parent) == null) (root = r).red = false; else if (pp.left == p) pp.left = r; else pp.right = r; r.left = p; p.parent = r; } return root; } static <K,V> TreeNode<K,V> rotateRight(TreeNode<K,V> root, TreeNode<K,V> p) { TreeNode<K,V> l, pp, lr; if (p != null && (l = p.left) != null) { if ((lr = p.left = l.right) != null) lr.parent = p; if ((pp = l.parent = p.parent) == null) (root = l).red = false; else if (pp.right == p) pp.right = l; else pp.left = l; l.right = p; p.parent = l; } return root; } static <K,V> TreeNode<K,V> balanceInsertion(TreeNode<K,V> root, TreeNode<K,V> x) { x.red = true; for (TreeNode<K,V> xp, xpp, xppl, xppr;;) { if ((xp = x.parent) == null) { x.red = false; return x; } else if (!xp.red || (xpp = xp.parent) == null) return root; if (xp == (xppl = xpp.left)) { if ((xppr = xpp.right) != null && xppr.red) { xppr.red = false; xp.red = false; xpp.red = true; x = xpp; } else { if (x == xp.right) { root = rotateLeft(root, x = xp); xpp = (xp = x.parent) == null ? null : xp.parent; } if (xp != null) { xp.red = false; if (xpp != null) { xpp.red = true; root = rotateRight(root, xpp); } } } } else { if (xppl != null && xppl.red) { xppl.red = false; xp.red = false; xpp.red = true; x = xpp; } else { if (x == xp.left) { root = rotateRight(root, x = xp); xpp = (xp = x.parent) == null ? null : xp.parent; } if (xp != null) { xp.red = false; if (xpp != null) { xpp.red = true; root = rotateLeft(root, xpp); } } } } } } static <K,V> TreeNode<K,V> balanceDeletion(TreeNode<K,V> root, TreeNode<K,V> x) { for (TreeNode<K,V> xp, xpl, xpr;;) { if (x == null || x == root) return root; else if ((xp = x.parent) == null) { x.red = false; return x; } else if (x.red) { x.red = false; return root; } else if ((xpl = xp.left) == x) { if ((xpr = xp.right) != null && xpr.red) { xpr.red = false; xp.red = true; root = rotateLeft(root, xp); xpr = (xp = x.parent) == null ? null : xp.right; } if (xpr == null) x = xp; else { TreeNode<K,V> sl = xpr.left, sr = xpr.right; if ((sr == null || !sr.red) && (sl == null || !sl.red)) { xpr.red = true; x = xp; } else { if (sr == null || !sr.red) { if (sl != null) sl.red = false; xpr.red = true; root = rotateRight(root, xpr); xpr = (xp = x.parent) == null ? null : xp.right; } if (xpr != null) { xpr.red = (xp == null) ? false : xp.red; if ((sr = xpr.right) != null) sr.red = false; } if (xp != null) { xp.red = false; root = rotateLeft(root, xp); } x = root; } } } else { // symmetric if (xpl != null && xpl.red) { xpl.red = false; xp.red = true; root = rotateRight(root, xp); xpl = (xp = x.parent) == null ? null : xp.left; } if (xpl == null) x = xp; else { TreeNode<K,V> sl = xpl.left, sr = xpl.right; if ((sl == null || !sl.red) && (sr == null || !sr.red)) { xpl.red = true; x = xp; } else { if (sl == null || !sl.red) { if (sr != null) sr.red = false; xpl.red = true; root = rotateLeft(root, xpl); xpl = (xp = x.parent) == null ? null : xp.left; } if (xpl != null) { xpl.red = (xp == null) ? false : xp.red; if ((sl = xpl.left) != null) sl.red = false; } if (xp != null) { xp.red = false; root = rotateRight(root, xp); } x = root; } } } } } /** * 递归检查,确保构造的是正确无误的红黑树 */ static <K,V> boolean checkInvariants(TreeNode<K,V> t) { TreeNode<K,V> tp = t.parent, tl = t.left, tr = t.right, tb = t.prev, tn = (TreeNode<K,V>)t.next; if (tb != null && tb.next != t) return false; if (tn != null && tn.prev != t) return false; if (tp != null && t != tp.left && t != tp.right) return false; if (tl != null && (tl.parent != t || tl.hash > t.hash)) return false; if (tr != null && (tr.parent != t || tr.hash < t.hash)) return false; if (t.red && tl != null && tl.red && tr != null && tr.red) return false; if (tl != null && !checkInvariants(tl)) return false; if (tr != null && !checkInvariants(tr)) return false; return true; } // Unsafe相关的初始化工作 private static final sun.misc.Unsafe U; private static final long LOCKSTATE; static { try { U = sun.misc.Unsafe.getUnsafe(); Class<?> k = TreeBin.class; LOCKSTATE = U.objectFieldOffset (k.getDeclaredField("lockState")); } catch (Exception e) { throw new Error(e); } } }

static final class ReservationNode<K,V> extends Node<K,V> { ReservationNode() { super(RESERVED, null, null, null); } Node<K,V> find(int h, Object k) { return null; } }
首先介绍一些基本的方法,这些方法不会直接用到,但却是理解ConcurrentHashMap常见方法前提,因为这些方法被ConcurrentHashMap常见的方法调用。然后在介绍完这些基本方法的基础上,再分析常见的containsValue、put、remove等常见方法。

private final Node<K,V>[] initTable() { Node<K,V>[] tab; int sc; while ((tab = table) == null || tab.length == 0) { if ((sc = sizeCtl) < 0) //真正的初始化是要禁止并发的,保证tables数组只被初始化一次,但又不能切换线程,所以需要yield()让出CPU Thread.yield(); // lost initialization race; just spin else if (U.compareAndSwapInt(this, SIZECTL, sc, -1)) { //更新sizeCtl标识为初始化状态 try { //如果当前表为空,初始化table表 if ((tab = table) == null || tab.length == 0) { int n = (sc > 0) ? sc : DEFAULT_CAPACITY; @SuppressWarnings("unchecked") Node<K,V>[] nt = (Node<K,V>[])new Node<?,?>[n]; table = tab = nt; sc = n - (n >>> 2); //设置阈值为总长度的0.75,从而可看出loadFactor没有用到 } } finally { sizeCtl = sc; //设置阈值 } break; } } return tab; }

//volatile读取table[i] static final <K,V> Node<K,V> tabAt(Node<K,V>[] tab, int i) { return (Node<K,V>)U.getObjectVolatile(tab, ((long)i << ASHIFT) + ABASE); } //CAS更新table[i],更新Node链表的头节点,或者TreeBin节点 static final <K,V> boolean casTabAt(Node<K,V>[] tab, int i, Node<K,V> c, Node<K,V> v) { return U.compareAndSwapObject(tab, ((long)i << ASHIFT) + ABASE, c, v); } //volatile写入table[i] static final <K,V> void setTabAt(Node<K,V>[] tab, int i, Node<K,V> v) { U.putObjectVolatile(tab, ((long)i << ASHIFT) + ABASE, v); } //尝试将链表转化为红黑树 private final void treeifyBin(Node<K,V>[] tab, int index) { Node<K,V> b; int n, sc; if (tab != null) { //当table的length小于64时,只进行一次扩容 if ((n = tab.length) < MIN_TREEIFY_CAPACITY) tryPresize(n << 1); //将链表转化为红黑树 else if ((b = tabAt(tab, index)) != null && b.hash >= 0) { synchronized (b) { if (tabAt(tab, index) == b) { TreeNode<K,V> hd = null, tl = null; for (Node<K,V> e = b; e != null; e = e.next) { TreeNode<K,V> p = new TreeNode<K,V>(e.hash, e.key, e.val, null, null); if ((p.prev = tl) == null) hd = p; else tl.next = p; tl = p; } setTabAt(tab, index, new TreeBin<K,V>(hd)); } } } } } //将红黑树转化为链表,在调用此方法时synchronized加锁,这里不再需要加锁 static <K,V> Node<K,V> untreeify(Node<K,V> b) { Node<K,V> hd = null, tl = null; for (Node<K,V> q = b; q != null; q = q.next) { Node<K,V> p = new Node<K,V>(q.hash, q.key, q.val, null); if (tl == null) hd = p; else tl.next = p; tl = p; } return hd; }

int n = tab.length, stride; if ((stride = (NCPU > 1) ? (n >>> 3) / NCPU : n) < MIN_TRANSFER_STRIDE) stride = MIN_TRANSFER_STRIDE; // 最小值为16
计算完成之后每个transfer按照计算的值处理相应下标位置的桶,扩容操作从旧数组的末尾向前一次对hash桶进行处理。从末尾向前处理主要是减少和遍历数据时的锁冲突。从旧数组的末尾向前代码如下:

//标记一个transfer任务是否完成,完成为true,否则为false boolean advance = true; //标记整个扩容任务是否完成 boolean finishing = false; // to ensure sweep before committing nextTab //仅截取部分代码片段,其中i表示当前transfer处理的hash桶的index,而bound表示当前transfer需要处理的hash桶的index的下界 while (advance) { int nextIndex, nextBound; if (--i >= bound || finishing) //表明一次transfer未执行完毕 advance = false; else if ((nextIndex = transferIndex) <= 0) { //transfer任务完成,可以准备退出扩容 i = -1; advance = false; } //尝试申请transfer任务 else if (U.compareAndSwapInt (this, TRANSFERINDEX, nextIndex, nextBound = (nextIndex > stride ? nextIndex - stride : 0))) { bound = nextBound; //transfer任务中hash桶的下界 i = nextIndex - 1; //transfer当前处理的hash桶的index advance = false; } }
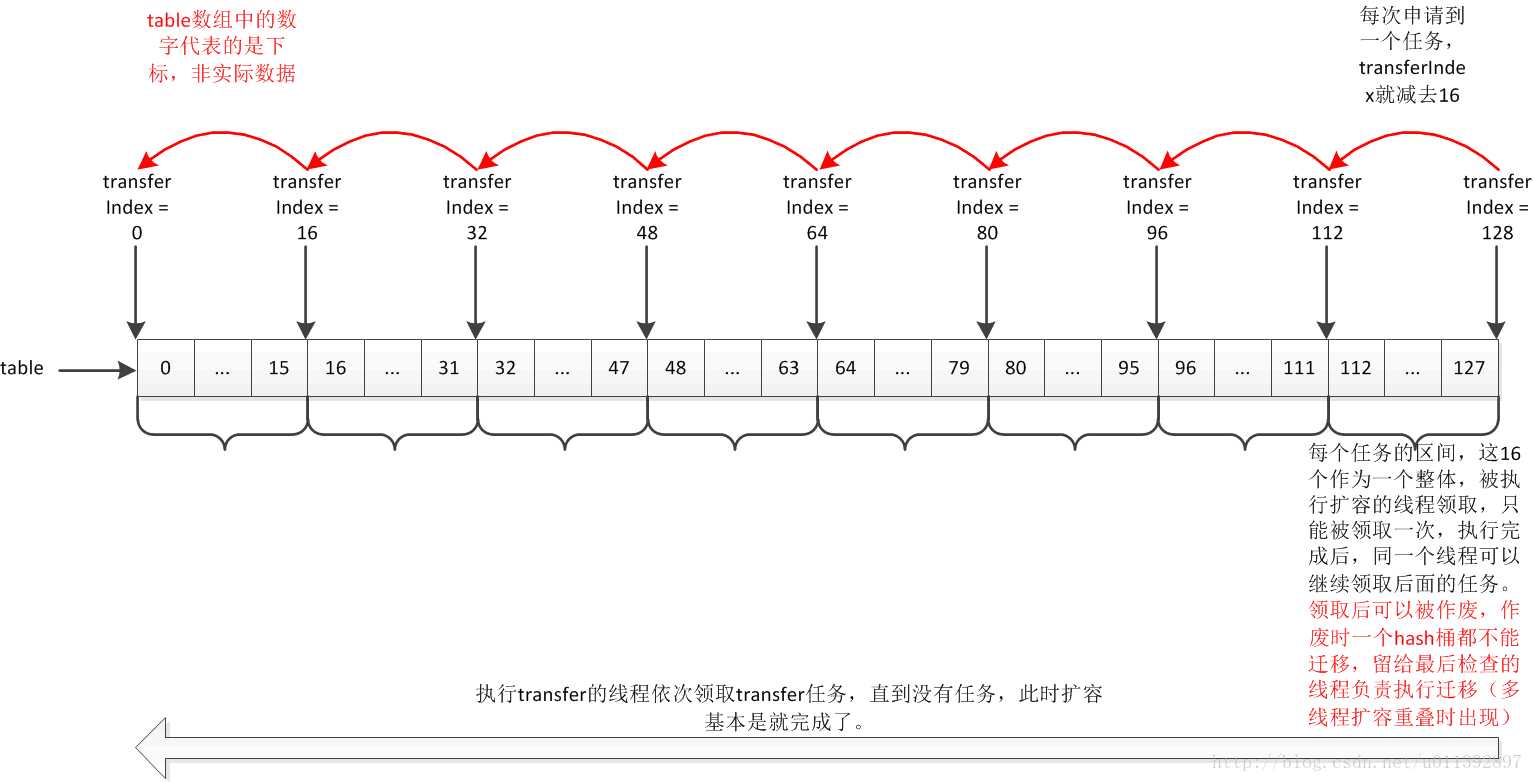
扩容部分的完整代码如下:

//x表示扩容需要增加的值 //check表示计数操作是否会触发扩容,check<0表示不会触发 //check<=1说明线程更新计数时没有遇到竞争 private final void addCount(long x, int check) { CounterCell[] as; long b, s; if ((as = counterCells) != null || !U.compareAndSwapLong(this, BASECOUNT, b = baseCount, s = b + x)) { CounterCell a; long v; int m; boolean uncontended = true; if (as == null || (m = as.length - 1) < 0 || (a = as[ThreadLocalRandom.getProbe() & m]) == null || !(uncontended = U.compareAndSwapLong(a, CELLVALUE, v = a.value, v + x))) { fullAddCount(x, uncontended); return; } if (check <= 1) return; s = sumCount(); } if (check >= 0) { //检测是否扩容 Node<K,V>[] tab, nt; int n, sc; //扩容基本条件 while (s >= (long)(sc = sizeCtl) && (tab = table) != null && (n = tab.length) < MAXIMUM_CAPACITY) { int rs = resizeStamp(n); //计算本次扩容生成戳 if (sc < 0) { //表明此时没有其他线程扩容 //5个条件只要有一个为true,则当前线程不能帮助扩容 if ((sc >>> RESIZE_STAMP_SHIFT) != rs || sc == rs + 1 || sc == rs + MAX_RESIZERS || (nt = nextTable) == null || transferIndex <= 0) break; //前5个条件都为false时尝试此次扩容,将正在执行transfer任务的线程数+1 if (U.compareAndSwapInt(this, SIZECTL, sc, sc + 1)) transfer(tab, nt); } //尝试让当前线程成为第一个执行transfer任务的线程 else if (U.compareAndSwapInt(this, SIZECTL, sc, (rs << RESIZE_STAMP_SHIFT) + 2)) transfer(tab, null); //执行扩容 s = sumCount(); //重新计数看是否需要下一次扩容 } } } /** * Helps transfer if a resize is in progress. * 如果正在进行扩容,则尝试帮助执行transfer任务 */ final Node<K,V>[] helpTransfer(Node<K,V>[] tab, Node<K,V> f) { Node<K,V>[] nextTab; int sc; //判断是否仍然在执行扩容 if (tab != null && (f instanceof ForwardingNode) && (nextTab = ((ForwardingNode<K,V>)f).nextTable) != null) { int rs = resizeStamp(tab.length); //计算扩容生成戳 //再次判断是否正在执行扩容 while (nextTab == nextTable && table == tab && (sc = sizeCtl) < 0) { // 判断下是否能真正帮助此次扩容 if ((sc >>> RESIZE_STAMP_SHIFT) != rs || sc == rs + 1 || sc == rs + MAX_RESIZERS || transferIndex <= 0) break; //不能帮助则终止 if (U.compareAndSwapInt(this, SIZECTL, sc, sc + 1)) { transfer(tab, nextTab); //否则执行此次扩容 break; } } return nextTab; //返回扩容后的数组 } return table; //如果是返回table说明扩容已经结束,table被其它线程赋值新数组 } //预先扩容,包含初始化逻辑的扩容 //用于putAll,此时是需要考虑初始化;链表转化为红黑树中,不满足table容量条件时,进行一次扩容,此时就是普通的扩容 private final void tryPresize(int size) { int c = (size >= (MAXIMUM_CAPACITY >>> 1)) ? MAXIMUM_CAPACITY : tableSizeFor(size + (size >>> 1) + 1); int sc; while ((sc = sizeCtl) >= 0) { Node<K,V>[] tab = table; int n; if (tab == null || (n = tab.length) == 0) { //用于处理初始化,跟initTable方法相同 n = (sc > c) ? sc : c; if (U.compareAndSwapInt(this, SIZECTL, sc, -1)) { try { if (table == tab) { @SuppressWarnings("unchecked") Node<K,V>[] nt = (Node<K,V>[])new Node<?,?>[n]; table = nt; sc = n - (n >>> 2); } } finally { sizeCtl = sc; } } } // c <= sc,说明已经被扩容过了;n >= MAXIMUM_CAPACITY说明table数组已经到了最大长度 else if (c <= sc || n >= MAXIMUM_CAPACITY) break; else if (tab == table) { //可以进行扩容 int rs = resizeStamp(n); if (sc < 0) { Node<K,V>[] nt; if ((sc >>> RESIZE_STAMP_SHIFT) != rs || sc == rs + 1 || sc == rs + MAX_RESIZERS || (nt = nextTable) == null || transferIndex <= 0) break; if (U.compareAndSwapInt(this, SIZECTL, sc, sc + 1)) transfer(tab, nt); } else if (U.compareAndSwapInt(this, SIZECTL, sc, (rs << RESIZE_STAMP_SHIFT) + 2)) transfer(tab, null); } } } // 执行节点迁移,准确地说是迁移内容,因为很多节点都需要进行复制,复制能够保证读操作尽量不受影响 private final void transfer(Node<K,V>[] tab, Node<K,V>[] nextTab) { int n = tab.length, stride; if ((stride = (NCPU > 1) ? (n >>> 3) / NCPU : n) < MIN_TRANSFER_STRIDE) stride = MIN_TRANSFER_STRIDE; //计算每个transfer负责处理多少个hash桶 if (nextTab == null) { //初始化Node数组 try { @SuppressWarnings("unchecked") Node<K,V>[] nt = (Node<K,V>[])new Node<?,?>[n << 1]; nextTab = nt; } catch (Throwable ex) { // try to cope with OOME sizeCtl = Integer.MAX_VALUE; return; } nextTable = nextTab; transferIndex = n; } int nextn = nextTab.length; // 转发节点,在旧数组的一个hash桶中所有节点都被迁移完后,放置在这个hash桶中,表明已经迁移完,对它的读操作会转发到新数组 ForwardingNode<K,V> fwd = new ForwardingNode<K,V>(nextTab); boolean advance = true; boolean finishing = false; //标识扩容工作是否完成 for (int i = 0, bound = 0;;) { Node<K,V> f; int fh; while (advance) { int nextIndex, nextBound; if (--i >= bound || finishing) // 一次transfer还未执行完毕 advance = false; else if ((nextIndex = transferIndex) <= 0) { // transfer任务已经没有了,表明可以准备退出扩容了 i = -1; advance = false; } //尝试申请transfer任务 else if (U.compareAndSwapInt (this, TRANSFERINDEX, nextIndex, nextBound = (nextIndex > stride ? nextIndex - stride : 0))) { // transfer申请到任务后标记自己的任务区间 bound = nextBound; i = nextIndex - 1; advance = false; } } //处理扩容重叠 if (i < 0 || i >= n || i + n >= nextn) { int sc; if (finishing) { //扩容完成 nextTable = null; table = nextTab; sizeCtl = (n << 1) - (n >>> 1); return; } // 尝试把正在执行扩容的线程数减1,表明自己要退出扩容 if (U.compareAndSwapInt(this, SIZECTL, sc = sizeCtl, sc - 1)) { // 判断下自己是不是本轮扩容中的最后一个线程,如果不是,则直接退出。 if ((sc - 2) != resizeStamp(n) << RESIZE_STAMP_SHIFT) return; finishing = advance = true; //最后一个扩容的线程要重新检查一次旧数组的所有hash桶,看是否是都被正确迁移到新数组了。 // 正常情况下,重新检查时,旧数组所有hash桶都应该是转发节点,此时这个重新检查的工作很快就会执行完。 // 特殊情况,比如扩容重叠,那么会有线程申请到了transfer任务,但是参数错误(旧数组和新数组对不上,不是2倍长度的关系), // 此时这个线程领取的任务会作废,那么最后检查时,还要处理因为作废二没有被迁移的hash桶,把它们正确迁移到新数组中 i = n; // recheck before commit } } else if ((f = tabAt(tab, i)) == null) // hash桶本身为null,不用迁移,直接尝试安放一个转发节点 advance = casTabAt(tab, i, null, fwd); else if ((fh = f.hash) == MOVED) //当前hash桶有线程在对其扩容 advance = true; // already processed else { synchronized (f) { //给f加锁 // 判断下加锁的节点仍然是hash桶中的第一个节点,加锁的是第一个节点才算加锁成功 if (tabAt(tab, i) == f) { Node<K,V> ln, hn; if (fh >= 0) { int runBit = fh & n; //记录当前hash值的第X(Math.pow(2,X)=n)位的值 Node<K,V> lastRun = f; for (Node<K,V> p = f.next; p != null; p = p.next) { int b = p.hash & n; if (b != runBit) { runBit = b; lastRun = p; } } if (runBit == 0) { ln = lastRun; hn = null; } else { hn = lastRun; ln = null; } for (Node<K,V> p = f; p != lastRun; p = p.next) { int ph = p.hash; K pk = p.key; V pv = p.val; if ((ph & n) == 0) ln = new Node<K,V>(ph, pk, pv, ln); else hn = new Node<K,V>(ph, pk, pv, hn); } setTabAt(nextTab, i, ln); // 放在新table的hash桶中 setTabAt(nextTab, i + n, hn); // 放在新table的hash桶中 setTabAt(tab, i, fwd); // 把旧table的hash桶中放置转发节点,表明此hash桶已经被处理 advance = true; } // 红黑树的情况,先使用链表的方式遍历,复制所有节点,根据高低位 //组装成两个链表lo和hi,然后看下是否需要进行红黑树变换,最后放在新数组对应的hash桶中 else if (f instanceof TreeBin) { TreeBin<K,V> t = (TreeBin<K,V>)f; TreeNode<K,V> lo = null, loTail = null; TreeNode<K,V> hi = null, hiTail = null; int lc = 0, hc = 0; for (Node<K,V> e = t.first; e != null; e = e.next) { int h = e.hash; TreeNode<K,V> p = new TreeNode<K,V> (h, e.key, e.val, null, null); //当前节点的hash值第X位为0 if ((h & n) == 0) { if ((p.prev = loTail) == null) lo = p; else loTail.next = p; loTail = p; ++lc; } //当前节点的hash值第X位为1 else { if ((p.prev = hiTail) == null) hi = p; else hiTail.next = p; hiTail = p; ++hc; } } //如果lo的size(lc)小于6,则将lo转化为链表 //如果lo的size大于6且hi的size(hc)不等于0,重新构造红黑树,如果hi的size为0,则ln为原始红黑树 ln = (lc <= UNTREEIFY_THRESHOLD) ? untreeify(lo) : (hc != 0) ? new TreeBin<K,V>(lo) : t; //hn的设置桶ln相同 hn = (hc <= UNTREEIFY_THRESHOLD) ? untreeify(hi) : (lc != 0) ? new TreeBin<K,V>(hi) : t; setTabAt(nextTab, i, ln); setTabAt(nextTab, i + n, hn); setTabAt(tab, i, fwd); advance = true; } } } } } }
如下是一个链表扩容的示意图,第一张是一个hash桶中的一条链表,其中蓝色节点表示第X位为0,而红色表示第X位为1,扩容后旧table[i]的桶中为一个ForwardingNode节点,而新nextTab[i]和nextTable[i+n]的桶中分别为第二张和第三张图。

static class Traverser<K,V> { Node<K,V>[] tab; // current table; updated if resized 扩容完成后的旧数组 Node<K,V> next; // the next entry to use 扩容完成后的新数组 TableStack<K,V> stack, spare; //存储遍历到的 ForwardingNodes int index; // index of bin to use next 下一个要读取的hash桶的下标 int baseIndex; // current index of initial table 起始下标 int baseLimit; // index bound for initial table 终止下标 final int baseSize; // initial table size tab数组长度 Traverser(Node<K,V>[] tab, int size, int index, int limit) { this.tab = tab; this.baseSize = size; this.baseIndex = this.index = index; this.baseLimit = limit; this.next = null; } /** * Advances if possible, returning next valid node, or null if none. * 遍历器指针移动到下一个有实际数据的节点,并返回该节点,如果结束则返回null */ final Node<K,V> advance() { Node<K,V> e; if ((e = next) != null) e = e.next; for (;;) { Node<K,V>[] t; int i, n; // must use locals in checks if (e != null) return next = e; //节点非空则直接返回该节点 //达到边界条件直接返回null if (baseIndex >= baseLimit || (t = tab) == null || (n = t.length) <= (i = index) || i < 0) return next = null; //处理特殊节点(ForwardingNode、TreeBin、ReservationNode) if ((e = tabAt(t, i)) != null && e.hash < 0) { if (e instanceof ForwardingNode) { //遍历ForwardingNode的nextTable tab = ((ForwardingNode<K,V>)e).nextTable; e = null; pushState(t, i, n); //将当前位置入栈 continue; } else if (e instanceof TreeBin) e = ((TreeBin<K,V>)e).first; else e = null; } if (stack != null) recoverState(n); //栈不为空,出栈 else if ((index = i + baseSize) >= n) //栈为空,遍历下一个hash桶 index = ++baseIndex; // visit upper slots if present } } /** * Saves traversal state upon encountering a forwarding node. * 入栈操作,保存当前对tab的遍历信息 */ private void pushState(Node<K,V>[] t, int i, int n) { TableStack<K,V> s = spare; // reuse if possible if (s != null) spare = s.next; else s = new TableStack<K,V>(); s.tab = t; s.length = n; s.index = i; s.next = stack; stack = s; } /** * Possibly pops traversal state. * 参数n为当前tab数组的长度 * 可能会出栈,不出栈时,更改索引,准备遍历的是FN.nextTable中对应的第二个hash桶 */ private void recoverState(int n) { TableStack<K,V> s; int len; while ((s = stack) != null && (index += (len = s.length)) >= n) { n = len; index = s.index; tab = s.tab; s.tab = null; TableStack<K,V> next = s.next; s.next = spare; // save for reuse stack = next; spare = s; } if (s == null && (index += baseSize) >= n) index = ++baseIndex; } }

public boolean containsValue(Object value) { if (value == null) throw new NullPointerException(); Node<K,V>[] t; if ((t = table) != null) { Traverser<K,V> it = new Traverser<K,V>(t, t.length, 0, t.length); for (Node<K,V> p; (p = it.advance()) != null; ) { V v; if ((v = p.val) == value || (v != null && value.equals(v))) return true; } } return false; }

public boolean containsKey(Object key) { return get(key) != null; } public V get(Object key) { Node<K,V>[] tab; Node<K,V> e, p; int n, eh; K ek; int h = spread(key.hashCode()); if ((tab = table) != null && (n = tab.length) > 0 && (e = tabAt(tab, (n - 1) & h)) != null) { if ((eh = e.hash) == h) { if ((ek = e.key) == key || (ek != null && key.equals(ek))) return e.val; } else if (eh < 0) //当hash值小于0时,说明当前节点为特殊节点,则以当前节点为根节点进行遍历,而不是遍历该节点的next节点 return (p = e.find(h, key)) != null ? p.val : null; while ((e = e.next) != null) { if (e.hash == h && ((ek = e.key) == key || (ek != null && key.equals(ek)))) return e.val; } } return null; }

public V put(K key, V value) { return putVal(key, value, false); } final V putVal(K key, V value, boolean onlyIfAbsent) { if (key == null || value == null) throw new NullPointerException(); //键或值存在null时直接抛出空指针异常 int hash = spread(key.hashCode()); int binCount = 0; for (Node<K,V>[] tab = table;;) { Node<K,V> f; int n, i, fh; if (tab == null || (n = tab.length) == 0) tab = initTable(); //初始化table else if ((f = tabAt(tab, i = (n - 1) & hash)) == null) { if (casTabAt(tab, i, null, new Node<K,V>(hash, key, value, null))) break; // no lock when adding to empty bin } else if ((fh = f.hash) == MOVED) tab = helpTransfer(tab, f); //发现转发节点,帮助扩容 else { V oldVal = null; synchronized (f) { if (tabAt(tab, i) == f) { if (fh >= 0) { //当前hash值大于0说明hash桶中为链表 binCount = 1; for (Node<K,V> e = f;; ++binCount) { K ek; if (e.hash == hash && ((ek = e.key) == key || (ek != null && key.equals(ek)))) { oldVal = e.val; //如果当前键值对存在,则更新value为最新的value值 if (!onlyIfAbsent) e.val = value; break; } Node<K,V> pred = e; if ((e = e.next) == null) { pred.next = new Node<K,V>(hash, key, value, null); break; } } } else if (f instanceof TreeBin) { //hash桶值为红黑树 Node<K,V> p; binCount = 2; if ((p = ((TreeBin<K,V>)f).putTreeVal(hash, key, value)) != null) { oldVal = p.val; if (!onlyIfAbsent) p.val = value; } } } } if (binCount != 0) { //如果当前hash桶中的size大于8,将该链表转化为红黑树 if (binCount >= TREEIFY_THRESHOLD) treeifyBin(tab, i); if (oldVal != null) return oldVal; break; } } } addCount(1L, binCount); //计数值加1 return null; }

public V remove(Object key) { return replaceNode(key, null, null); } final V replaceNode(Object key, V value, Object cv) { int hash = spread(key.hashCode()); for (Node<K,V>[] tab = table;;) { Node<K,V> f; int n, i, fh; if (tab == null || (n = tab.length) == 0 || (f = tabAt(tab, i = (n - 1) & hash)) == null) break; //当前要移除的key不在table中 else if ((fh = f.hash) == MOVED) tab = helpTransfer(tab, f); else { V oldVal = null; boolean validated = false; synchronized (f) { if (tabAt(tab, i) == f) { if (fh >= 0) { //hash桶中为链表 validated = true; for (Node<K,V> e = f, pred = null;;) { K ek; if (e.hash == hash && ((ek = e.key) == key || (ek != null && key.equals(ek)))) { V ev = e.val; if (cv == null || cv == ev || (ev != null && cv.equals(ev))) { oldVal = ev; if (value != null) //如果当前value不为空,则更新value e.val = value; else if (pred != null) //value为空,则删除该节点 pred.next = e.next; else setTabAt(tab, i, e.next); //删除的是hash的第一个Node } break; } pred = e; if ((e = e.next) == null) break; } } else if (f instanceof TreeBin) { //hash桶为红黑树 validated = true; TreeBin<K,V> t = (TreeBin<K,V>)f; TreeNode<K,V> r, p; if ((r = t.root) != null && (p = r.findTreeNode(hash, key, null)) != null) { V pv = p.val; if (cv == null || cv == pv || (pv != null && cv.equals(pv))) { oldVal = pv; if (value != null) p.val = value; else if (t.removeTreeNode(p)) //处理退化为链表的情况 setTabAt(tab, i, untreeify(t.first)); } } } } } //因为该方法可能是执行替换也可能是删除,如果是删除操作则计数值减1 if (validated) { if (oldVal != null) { if (value == null) addCount(-1L, -1); return oldVal; } break; } } } return null; }
至此ConcurrentHashMap的主要方法也就介绍完了,综合比较Hashtable和ConcurrentHashMap,两者都是线程安全的,但是Hashtable是表级锁,而ConcurrentHashMap是段级锁,锁住的单个Node,而且ConcurrentHashMap可以并发读取。对整张表进行迭代时,ConcurrentHashMap使用了不同于Hashtable的迭代方式,而是一种弱一致性的迭代器。
Hashtable、ConcurrentHashMap源码分析
标签:通知 shift abs pointer state 数据结构 冲突 equals unpark
原文地址:http://www.cnblogs.com/zhanglei93/p/6760426.html