标签:style blog http color os io for ar art
poj2987 Firing http://poj.org/problem?id=2987
最大权闭合图模板题。闭合图就是,对于一个点集V,如果他们的所有的边所指向的点都在点集V中,则这个点集加上他们的边是闭合图。
这种题就是每个点有权值正负零都有可能,选某个点u,如果必须选v,则我们设u,v有一条有向边。最后要我们有一种选取方案使得所选的点权值和最大。这就是最大权闭合图。
解法用的是最大流来解。
最大流==最小割
最小割=减掉流量总和最少的一些边使得源点s和汇点t不连通。
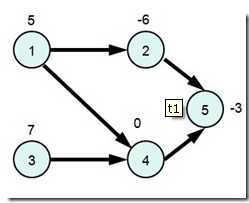
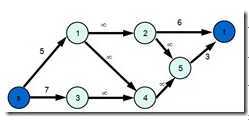
建图方法是:s源点到所有正权点连流量为那个点权值的边,所有负权点到汇点t连流量为负权绝对值的边。原来图中的依赖关系正常建边,流量定为inf。
跑出来的最大流就是最小割。用所有正权的和减去最小割就是可获得的最大权。
证明,因为中间的都是inf,所以最小割肯定是割到与s连的或者与t连的边。那么就是我们选择一些正权或者负权,并且我们都是选小的。也就是说对于正权到s这里,如果正权很小,并且选他就必须选一些负权很大的边,那么我们在最小割中也会选这个正权小的,使得st不连通。反之,如果负权那里小,我们就会选择割负权。最后正权的总和减去最小割。

1 #include<cstdio> 2 #include<cstring> 3 #include<queue> 4 #define mt(a,b) memset(a,b,sizeof(a)) 5 using namespace std; 6 typedef __int64 LL; 7 const LL inf=0x3f3f3f3f3f3f3f3fLL; 8 class Dinic { ///最大流(MV^2*ME) 9 typedef LL typef;///流量的类型 10 static const int ME=1000000;///边的个数 11 static const int MV=5010;///点的个数 12 int temp[MV],cur[MV],level[MV],path[MV]; 13 bool used[MV]; 14 queue<int> q; 15 typef flow; 16 bool bfs(int s,int t) { 17 mt(level,-1); 18 while(!q.empty()) q.pop(); 19 q.push(s); 20 level[s]=1; 21 while(!q.empty()) { 22 int u=q.front(); 23 q.pop(); 24 for(int i=g.head[u]; ~i; i=g.e[i].next) { 25 int v=g.e[i].v; 26 if(level[v]==-1&&g.e[i].flow) { 27 level[v]=level[u]+1; 28 q.push(v); 29 if(v==t) return true; 30 } 31 } 32 } 33 return false; 34 } 35 public: 36 struct G { 37 struct E { 38 int u,v,next; 39 typef flow; 40 } e[ME]; 41 int le,head[MV]; 42 void init() { 43 le=0; 44 mt(head,-1); 45 } 46 void add(int u,int v,typef flow) { 47 e[le].u=u; 48 e[le].v=v; 49 e[le].flow=flow; 50 e[le].next=head[u]; 51 head[u]=le++; 52 } 53 } g; 54 public: 55 typef getflow() { 56 return flow; 57 } 58 void init() { 59 g.init(); 60 } 61 void add(int u,int v,typef flow) { 62 g.add(u,v,flow); 63 g.add(v,u,0); 64 } 65 void solve(int s,int t) { 66 int p,tempp; 67 typef now; 68 bool flag; 69 flow=0; 70 while(bfs(s,t)) { 71 for(int i=0; i<MV; i++) { 72 temp[i]=g.head[i]; 73 used[i]=true; 74 } 75 p=1; 76 path[p]=s; 77 while(p) { 78 int u=path[p]; 79 if(u==t) { 80 now=inf; 81 for(int i=1; i<p; i++) { 82 now=min(now,g.e[cur[path[i]]].flow); 83 } 84 flow+=now; 85 for(int i=1; i<p; i++) { 86 int j=cur[path[i]]; 87 g.e[j].flow-=now; 88 g.e[j^1].flow+=now; 89 if(!g.e[j].flow) tempp=i; 90 } 91 p=tempp; 92 } else { 93 flag=false; 94 for(int i=temp[u]; ~i; i=g.e[i].next) { 95 int v=g.e[i].v; 96 if(used[v]&&g.e[i].flow&&level[u]+1==level[v]) { 97 cur[u]=i; 98 temp[u]=g.e[i].next; 99 flag=true; 100 path[++p]=v; 101 break; 102 } 103 } 104 if(flag) continue; 105 p--; 106 used[u]=false; 107 } 108 } 109 } 110 } 111 } dinic; 112 bool vis[5010]; 113 void dfs(int u,int t) { 114 if(u==t) return ; 115 vis[u]=true; 116 for(int i=dinic.g.head[u]; ~i; i=dinic.g.e[i].next) { 117 int v=dinic.g.e[i].v; 118 if(dinic.g.e[i].flow&&!vis[v]) { 119 dfs(v,t); 120 } 121 } 122 } 123 int main() { 124 int n,m; 125 while(~scanf("%d%d",&n,&m)) { 126 dinic.init(); 127 LL sum=0; 128 int s=0,t=n+1; 129 for(int i=1,val; i<=n; i++) { 130 scanf("%d",&val); 131 if(val>0) { 132 sum+=val; 133 dinic.add(s,i,val); 134 } else { 135 dinic.add(i,t,-val); 136 } 137 } 138 while(m--) { 139 int u,v; 140 scanf("%d%d",&u,&v); 141 dinic.add(u,v,inf); 142 } 143 dinic.solve(s,t); 144 mt(vis,0); 145 dfs(s,t); 146 int ans=0; 147 for(int i=1; i<=n; i++) { 148 if(vis[i]) ans++; 149 } 150 printf("%d %I64d\n",ans,sum-dinic.getflow()); 151 } 152 return 0; 153 }
end
标签:style blog http color os io for ar art
原文地址:http://www.cnblogs.com/gaolzzxin/p/3936973.html