标签：output can table pairs another starting img end repair
City X consists of n vertical and n horizontal infinite roads, forming n × n intersections. Roads (both vertical and horizontal) are numbered from 1 to n, and the intersections are indicated by the numbers of the roads that form them.
Sand roads have long been recognized out of date, so the decision was made to asphalt them. To do this, a team of workers was hired and a schedule of work was made, according to which the intersections should be asphalted.
Road repairs are planned for n2 days. On the i-th day of the team arrives at the i-th intersection in the list and if none of the two roads that form the intersection were already asphalted they asphalt both roads. Otherwise, the team leaves the intersection, without doing anything with the roads.
According to the schedule of road works tell in which days at least one road will be asphalted.
Input
The first line contains integer n (1 ≤ n ≤ 50) — the number of vertical and horizontal roads in the city.
Next n2 lines contain the order of intersections in the schedule. The i-th of them contains two numbers h**i, v**i (1 ≤ h**i, v**i ≤ n), separated by a space, and meaning that the intersection that goes i-th in the timetable is at the intersection of the h**i-th horizontal and v**i-th vertical roads. It is guaranteed that all the intersections in the timetable are distinct.
Output
In the single line print the numbers of the days when road works will be in progress in ascending order. The days are numbered starting from 1.
Examples
input
2 1 1 1 2 2 1 2 2
output
1 4
input
1 1 1
output
1
Note
In the sample the brigade acts like that:
On the first day the brigade comes to the intersection of the 1-st horizontal and the 1-st vertical road. As none of them has been asphalted, the workers asphalt the 1-st vertical and the 1-st horizontal road;
On the second day the brigade of the workers comes to the intersection of the 1-st horizontal and the 2-nd vertical road. The 2-nd vertical road hasn‘t been asphalted, but as the 1-st horizontal road has been asphalted on the first day, the workers leave and do not asphalt anything;
On the third day the brigade of the workers come to the intersection of the 2-nd horizontal and the 1-st vertical road. The 2-nd horizontal road hasn‘t been asphalted but as the 1-st vertical road has been asphalted on the first day, the workers leave and do not asphalt anything;
On the fourth day the brigade come to the intersection formed by the intersection of the 2-nd horizontal and 2-nd vertical road. As none of them has been asphalted, the workers asphalt the 2-nd vertical and the 2-nd horizontal road.
Code:
1 #include <bits/stdc++.h> 2 using namespace std; 3 static const int MAXN = 66; 4 int n; 5 int vis1[MAXN]; 6 int vis2[MAXN]; 7 int x , y; 8 vector<int> ans; 9 int main() 10 { 11 //freopen("D:\\系统优化\\Desktop\\littlepea\\in.data" , "r" , stdin); 12 scanf("%d" , &n); 13 n *= n; 14 for(int i = 1 ; i <= n ; ++i) 15 { 16 scanf("%d%d" , &x , &y); 17 if(vis1[x] || vis2[y]) 18 continue; 19 ans.push_back(i); 20 vis1[x] = vis2[y] = 1; 21 } 22 for(auto i: ans) 23 printf("%d " , i); 24 }
Robot Doc is located in the hall, with n computers stand in a line, numbered from left to right from 1 to n. Each computer containsexactly one piece of information, each of which Doc wants to get eventually. The computers are equipped with a security system, so to crack the i-th of them, the robot needs to collect at least a**i any pieces of information from the other computers. Doc can hack the computer only if he is right next to it.
The robot is assembled using modern technologies and can move along the line of computers in either of the two possible directions, but the change of direction requires a large amount of resources from Doc. Tell the minimum number of changes of direction, which the robot will have to make to collect all n parts of information if initially it is next to computer with number 1.
It is guaranteed that there exists at least one sequence of the robot‘s actions, which leads to the collection of all information. Initially Doc doesn‘t have any pieces of information.
Input
The first line contains number n (1 ≤ n ≤ 1000). The second line contains n non-negative integers a1, a2, ..., a**n (0 ≤ a**i < n), separated by a space. It is guaranteed that there exists a way for robot to collect all pieces of the information.
Output
Print a single number — the minimum number of changes in direction that the robot will have to make in order to collect all n parts of information.
Examples
input
3 0 2 0
output
1
input
5 4 2 3 0 1
output
3
input
7 0 3 1 0 5 2 6
output
2
Note
In the first sample you can assemble all the pieces of information in the optimal manner by assembling first the piece of information in the first computer, then in the third one, then change direction and move to the second one, and then, having 2 pieces of information, collect the last piece.
In the second sample to collect all the pieces of information in the optimal manner, Doc can go to the fourth computer and get the piece of information, then go to the fifth computer with one piece and get another one, then go to the second computer in the same manner, then to the third one and finally, to the first one. Changes of direction will take place before moving from the fifth to the second computer, then from the second to the third computer, then from the third to the first computer.
In the third sample the optimal order of collecting parts from computers can look like that: 1->3->4->6->2->5->7.
Code:
1 #include <bits/stdc++.h> 2 using namespace std; 3 deque<int> dq[2]; 4 bool flag; 5 int n; 6 int eat; 7 int change; 8 int x; 9 int main() 10 { 11 scanf("%d" , &n); 12 for(int i = 1 ; i <= n ; ++i) 13 { 14 scanf("%d" , &x); 15 dq[0].push_back(x); 16 } 17 while(!dq[flag].empty()) 18 { 19 x = dq[flag].front(); 20 dq[flag].pop_front(); 21 if(x <= eat) 22 { 23 ++eat; 24 } 25 else 26 { 27 dq[!flag].push_front(x); 28 } 29 if(dq[flag].empty()) 30 { 31 flag = !flag; 32 if(!dq[flag].empty()) 33 ++change; 34 } 35 } 36 printf("%d" , change); 37 }
The GCD table G of size n × n for an array of positive integers a of length n is defined by formula
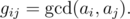
Let us remind you that the greatest common divisor (GCD) of two positive integers x and y is the greatest integer that is divisor of both xand y, it is denoted as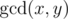 
. For example, for array a = {4, 3, 6, 2} of length 4 the GCD table will look as follows:
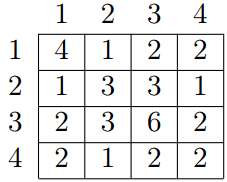
Given all the numbers of the GCD table G, restore array a.
Input
The first line contains number n (1 ≤ n ≤ 500) — the length of array a. The second line contains n2 space-separated numbers — the elements of the GCD table of G for array a.
All the numbers in the table are positive integers, not exceeding 109. Note that the elements are given in an arbitrary order. It is guaranteed that the set of the input data corresponds to some array a.
Output
In the single line print n positive integers — the elements of array a. If there are multiple possible solutions, you are allowed to print any of them.
Examples
input
4 2 1 2 3 4 3 2 6 1 1 2 2 1 2 3 2
output
4 3 6 2
input
1 42
output
42
input
2 1 1 1 1
output
1 1
Code:
1 #include <bits/stdc++.h> 2 using namespace std; 3 typedef long long LL; 4 static const int MAXN = 510 * 510; 5 map<int , int> mp; 6 LL data[MAXN]; 7 vector<LL> ans; 8 int n; 9 int main() 10 { 11 scanf("%I64d" , &n); 12 int t = n * n; 13 for(int i = 1 ; i <= t ; ++i) 14 { 15 scanf("%I64d" , &data[i]); 16 ++mp[data[i]]; 17 } 18 sort(data + 1 , data + 1 + t , [](LL a , LL b){return a > b;}); 19 for(int i = 1 ; i <= t ; ++i) 20 { 21 if(!mp[data[i]]) 22 continue; 23 --mp[data[i]]; 24 for(auto p: ans) 25 mp[__gcd(data[i] , p)] -= 2; 26 ans.push_back(data[i]); 27 } 28 for(auto x: ans) 29 printf("%I64d " , x); 30 }
2017-5-2-Train:Codeforces Round #323 (Div. 2)
标签：output can table pairs another starting img end repair
原文地址：http://www.cnblogs.com/jianglingxin/p/6827533.html
