标签:i+1 不容易 alt 梯度下降 lag 个数 连续 png 一点
机器学习中,感知机(perceptron)是一种二值的监督学习的算法(相应的函数,能决定输入是否属于某个分类,其中输入由一个数值向量表示)。感知机是一个线性分类器,其分类函数基于线性预测函数对新的输入作出预测,即,将输入(实数向量)映射到{-1,1}二值空间:
f(x)=sign(wx+b)
其中,sign是符号函数
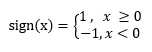
wx是w向量与x向量的内积,w向量与x向量均为n维,分别为如下形式
w=[w1,w2,...,wn]
x=[x1,x2,...,xn]T
不难发现,f(x)是n+1维欧氏空间的超平面,n维空间中的点被f(x)分为两部分(即两类),为了方便计算和表示,我们增加一个维度,使得b = w0x0, 其中x0=1,并且将w也写成列向量形式,则有,
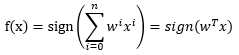
其中,w=[w0,w1,w2,...,wn]T
感知机学习的目的就是要找到一个perceptron,能把不同类别的点区分开来,具体来说就是,由训练数据集
T={(x1,y1), (x2,y2), ... , (xN, yN)}
其中N表示有N个数据,xi属于n+1维实数空间向量,yi属于{1, -1},求n+1维向量w
当然,这里需要有一个前提条件,训练数据要线性可分(比如如下图中的数据就不能线性可分)
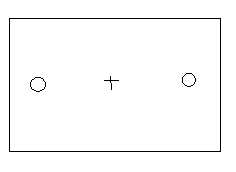 (n+1=3,假设圈圈表示y值为1,叉叉表示y值为-1,图中三点一线,线性不可分)
(n+1=3,假设圈圈表示y值为1,叉叉表示y值为-1,图中三点一线,线性不可分)
线性可分是指:
如果存在某个超平面wTx=0,对数据集中所有yi=1的数据,wTxi>0,对所有yi=-1的数据,wTxi<0,则这个数据集线性可分
定义(经验)损失函数(参数为w),并设法将损失函数极小化,比如损失函数为误分类点的个数,然后极小化为0,则就是找到一个符合要求的超平面。巴特,这样的损失函数不是关于w连续可导,不容易找。
如果选择损失函数为误分类点到超平面的总距离,那么当误分类点为0时,总距离也为0,分类正确。
输入空间一点x到超平面的距离为
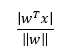
其中,||w||为w的L2范数,然后,对于误分类点来说,距离则为
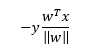
因为对于误分类点,y值与wTx符号相反,所以需要加个负号,股损失函数为误分类点总距离,假设误分类点集合为SetM,则,
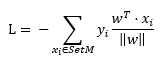
对于上式右边括号中的部分,我们可以认为分母是为了让wT归一化,而我们目的也是为了让SetM最终为空集合,从而使L为0,所以这里分母并没有什么影响,为了简单起见,这里将分母去掉,
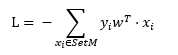
其中,SetM是误分类点集合,xi为n+1维列向量,w为n+1维列向量,yi为{1,-1}中的某个标量值,可以看出,误分类点越少,L越小,误分类点离超平面越近,L越小。当SetM为空集合(没有误分类点)时,L = 0,存在
误分类点时,在误分类点一定的情况下,L是w的线性函数。
采用随机梯度下降法,这是因为只有误分类的点参与优化w,优化过程中,一次选择一个误分类点使其梯度下降。
损失函数对w的偏导数为
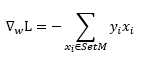
这是一个与xi一样的n维列向量,则针对某一个误分类点的梯度下降的优化为,
w← w + ayixi (*)
其中 + 号表示梯度下降,a表示步长,范围为(0,1],yi为第i个点的分类值(1,或者-1)。
还记得前面说的那个超平面的截距b吗?b其实就是这里的w0,因为x0=1,故
b←b + ayixi0 = b + ayi
当然了,这里b作为w的第0个分量,没必要单独列出来优化。
算法:
输入:训练数据集{(x1,y1), (x2,y2), ... , (xN, yN)},对某个数据点(xi,yi),检测条件 yiwxi > 0 是否满足,如果不满足表示是误分类点,则进行优化
输出:w 值
a) 当(xi, yi), yiwxi <= 0,则使用上面的(*)式对w进行优化,注意,xi的第0维值始终为1
b) 如果优化后依然yiwxi <= 0,则继续a),直到 yiwxi >0, 设置标志位flag 为true,表示有误差点
当然了,由于实际应用中,往往训练数据的x 是n维,可以将b 独立出来优化计算。
标签:i+1 不容易 alt 梯度下降 lag 个数 连续 png 一点
原文地址:http://www.cnblogs.com/sjjsxl/p/6834520.html