标签:logs log 自己 targe 部分 方法 target emma 原理
容斥原理(Inclusion–exclusion principle),是指在计数时,必须注意无一重复,无一遗漏,为了使重叠部分不被重复计算,人们研究出一种新的计数方法。这种方法的基本思想是:先不考虑重叠的情况,把包含于某内容中的所有对象的数目先计算出来,然后再把计数时重复计算的数目排斥出去,使得计算的结果既无遗漏又无重复,这种计数的方法称为容斥原理。——以上来自百度百科
设S为有限集,,则
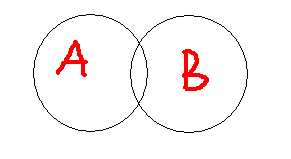
两个集合的容斥关系公式:A∪B=A+B-A∩B(∩:重合的部分)
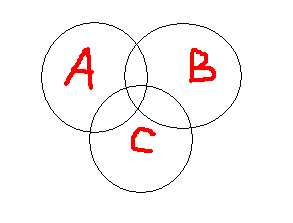
三个集合的容斥关系公式:A∪B∪C=A+B+C-A∩B-B∩C-C∩A+A∩B∩C
详细推理如下:
1、等式右边改造={[(A+B-A∩B)+C-B∩C]-C∩A}+A∩B∩C
2、分块标记如右图图:1245构成A,2356构成B,4567构成C
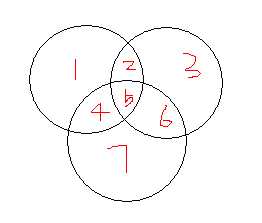
3、等式右边()里指的是下图的1+2+3+4+5+6六部分:
那么A∪B∪C还缺部分7。
4、等式右边[]号里+C(4+5+6+7)后,相当于A∪B∪C多加了4+5+6三部分,
减去B∩C(即5+6两部分)后,还多加了部分4。
5、等式右边{}里减去C∩A(即4+5两部分)后,A∪B∪C又多减了部分5,
如果被计数的事物有A、B两类,那么,A类B类元素个数总和=属于A类元素个数+属于B类元素个数—既是A类又是B类的元素个数。(A∪B=A+B-A∩B)
原理 2
如果被计数的事物有A、B、C三类,那么,A类和B类和C类元素个数总和=A类元素个数+B类元素个数+C类元素个数—既是A类又是B类的元素个数—既是A类又是C类的元素个数—既是B类又是C类的元素个数+既是A类又是B类而且是C类的元素个数。(A∪B∪C=A+B+C-A∩B-B∩C-C∩A+A∩B∩C)
自己选的路,跪着也要走完!!!
标签:logs log 自己 targe 部分 方法 target emma 原理
原文地址:http://www.cnblogs.com/wsdestdq/p/6839495.html