分布式深度学习之DC-ASGD

标签：too   exp   normal   网络学习   准备   频率   个数   number   ever   

本篇笔记是听刘铁岩老师做Distributed Deep Learning：New Driving Force of Artificial Intelligence报告整理而成

深度学习梯度下降公式如下

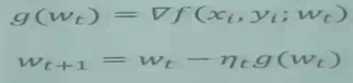
常用的深度学习训练方法为：

Full batch -> SGD -> min-batch SGD

Stochastic Gradient Descent (SGD)

 其中：

• full batch是将所有的样本过一遍再更新参数，更新的效率较低。
• SGD每一个样本更新一次参数，更新频率非常快。但是每一个样本对应的目标函数和整个数据集对应的目标函数是有差别的，因为这是一个随机抽样。可以证明，在随机抽样的时候SGD的目标函数对整个神经网络学习的目标函数来说是一个无偏估计，但这个无偏估计可能会有很大的方差，所以在学习的过程中会引入许多因方差导致的噪声，所以学习的收敛率不是很好。
• mini-batch是在这两者之间达到一个平衡，一方面希望比较频繁地更新参数，另一方面希望mini-batch降低单个样本带来的方差。

以上是标准的神经网络的训练方法。

challenges of training deep networks

• Overfitting: Too many parameters to learn from limited number of training examples 当一个网络变深的时候，该网络作为一个函数的容量程指数级增大，即当网络很深的时候，该网络的表达能力非常强。
• Gradient vanishing or exploding

上图是sigmoid导数的图像，该最大值为0.25，因此当级联导数时就会造成梯度消失。

方法二、Batch Normalization

在每一个隐节点做白化，并且是带参数的白化。做白化，让一批样本的均值为0。

sigmoid函数导数在x为0时取得最大值，因此让样本的均值为0，可以减缓梯度的vanishing

另一方面，通过对min-batch做白化，而不是对整个训练样本做，这样能有效地去除了不同的batch之间的差别。这样便去除了数据的复杂度，使得网络不用去费劲fit不同的样本，这样也能减缓overfit

方法3、在标准的cnn上加了直通通路，用带参的门函数控制网络是直连还是经过sigmoid。

Highway Network的思想来源于LSTM，它的作者也是LSTM的发明者。

类似地还有：

---

The Deeper, The Better ?

训练数据越大，最优层数越深。

大量数据如何训练？

经典结构：数据并行。把数据切成很多小份，每一份训练数据扔到一个机器上，在该机器上即可根据本地数据来做训练，通过梯度下降更新神经网络。当每一个局部得到一些神经网络的更新之后，希望大家共同协作训练。大家就会把自己学到的东西推送到一个公共的服务器上，服务器上就会看到所有的local machine送上来的东西，它会把他们做一个集成，集成了之后就会得到一个它认为考虑了所有的训练机器所有信息之后最好的模型的状态，然后再把最好的模型发送给每一个机器。然后每一个机器利用自己的局部参数去更新下一轮的数据。这样周而复始。这就是经典的参数服务器的构架。

Parameter Sever V.S. Data flow（tensor flow里面用的图计算）各有优缺点。

数据同步的好处：精确性

同步的并行实现等价于某一个串行的梯度下降法，只不过min-batch的size变了。

Synchronous data parallelization is slow due to the barrier, and will increase the effective mini-batch size of DNN training, which usually affects the classification accuracy.。但是训练速度总是受限于最慢的机器。

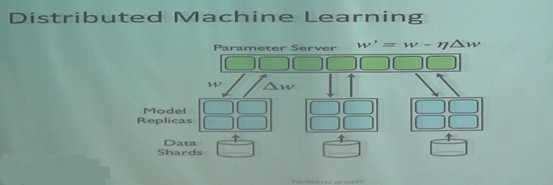
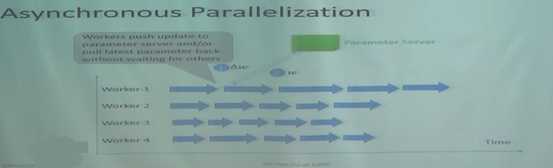
异步，每个机器算完自己的梯度就扔到服务器上，并不管服务器有没有来得及把大家加在一起更新模型，结果推送上去之后就继续往下走了，不去等别的机器，但过了一段时间觉得希望等别的机器的信息的时候，就把当时那个点上服务器上的模型拽下来，更新一下自己的起点，然后再往下走。每一台机器都这样走。

这个策略更新很快，而且不用担心服务器宕掉。但它的缺点是它的过程有点out of control，已经不是任何一种标准的Gradient Descent操作。一般称这种问题为delayed gradients。

Asynchronous data parallelization is fast due to no waiting time, but will suffer from delayed grandients(even if all machines have the same speed), which usually slows down the convergence.

有人证明过，因为有delayed gradients，虽然每一轮迭代的次数很快，但是整体的收敛的轮数变大了很多。

为了解决这个问题，人们使用了很多手段，包括SSP、AdaDelay等等。他们或者强制要求跑的快的机器停下来等待比较慢的机器，或者给延迟的梯度一个较小的学习率。

一台机器算得的g(W_(t))准备更新到服务器上的模型时，由于其他机器更新了模型，此时服务器上的W已经是W_(t+tao)。因为有delayed gradients，W_(t+tao)本来需要更新g(W_(t+tao))，而现在更新了g(W_(t))。

于是想到了泰勒展开。用g(W_(t))去表示g(W_(t+tao))。

一次项已经有了。二次项需要去计算。g(W_(t))是梯度，二次项就是梯度的梯度……这样就需要计算hessian matrix，而这个矩阵的计算复杂度远大于一次项梯度的计算。

首先，泰勒展开在什么时候有意义呢？Wt和Wt+τ距离不能太远，如果相差太远，那些高阶项就不是小量，有限泰勒展开就不准了。这决定了在训练的哪个阶段使用这项技术：在训练的后半程，当模型快要收敛，学习率较小的时候，可以保证每次模型变化不太大，从而安全地使用泰勒展开。

其次，即便是多加上一个一阶项，运算量也是很大的。因为梯度函数的一阶导数对应于原目标函数的二阶导数，也就是对应于海森阵。我们知道海森阵计算和存储的复杂度都很高，在模型很大的时候，实操性不强。

Is there any efficient way of computing the hissian matrix?

那么怎么解决这个挑战呢？我们证明了一个定理，在特定情况下，Hessen阵可以几乎0代价地计算出来，而且近似损失非常之小。具体而言，我们证明了对于一些特定的损失函数（负对数似然的形式），二阶导可以被一阶导的外积进行无偏估计。无偏估计虽然均值相同，方差可能仍然很大，为了进一步提升近似效果，我们通过最小化MSE来控制方差。做完之后我们就得到了一个新的公式，这个公式除了以前的异步的梯度下降以外还多引入一项，其中包含一个神奇的Φ函数和λ因子，只要通过调节他们就可以有效的补偿延迟。

在此基础上，我们进一步证明，使用延迟补偿的异步并行算法可以取得更好的收敛性质，其对延迟的敏感性大大降低。

这样就可以把异步的梯度下降做一个改进。

 

有了这样的思路后就可以做实验对比，通常单机版是收敛到最好的精度，一旦做多机并行，精度总会有所损失。如果做同步的多机并行，因为增大了batchsize所以会有精度损失，如果做异步的多机并行，因为其过程中会有gradient delay所以也会有精度损失。

实验效果：

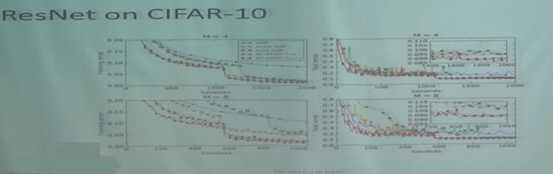
类似的一些研究

 

分布式深度学习之DC-ASGD

标签：too   exp   normal   网络学习   准备   频率   个数   number   ever   

原文地址：http://www.cnblogs.com/stjay/p/6848183.html