标签:class 分配 部分 适用于 ica rest [] 为我 实际应用
k近邻法(k-nearest neighbors algorigthm) 是一种最基本的用于分类和回归的方法之一,当没有关于训练数据的分布时,首先最容易想到的就是采用k近邻法。
k近邻法输入为实例的特征向量,输出为实例的类别。算法思想是,给定训练数据集,对应输入空间的各个数据点,要判断一个新的数据点的分类,则取目标数据点最近的k个数据点,
然后统计这k个数据点中每个分类各占多少,并取数量最多的那个分类作为目标数据点的分类。
上面说到的“最近”?那么何为最近?
k近邻法通常采用欧式距离来表征两个数据点的距离,距离越小,这两个数据点越近。
假设数据点x具有n维度(n个特征),
x=[x1,x2, ... , xn]T
数据xi和xj的距离则为
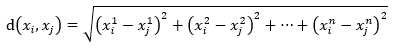
当然,还可以采用Minkowski距离,这是更一般的形式
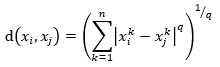
其中,q >= 1.
当q=1,为曼哈顿距离(Manhattan distance)
当q=2,为欧式距离(Euclidean distance)
当q=+∞,为两个点映射到各个坐标距离的最大值
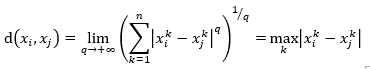
值得注意的是上面所说的距离适用于数据点的特征向量的(行列式)值是连续的,或者说向量各维度的值是连续的。
对于分类变量(categorical variables),则使用汉明距离(Hamming distance),
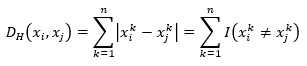
其中,x是n维向量,每个维度的取值为{0,1},为0或者为1,汉明距离就是统计对应各维度值不等的个数。
如果k值较小,则使用较小的邻域中的数据点进行预测,则近似误差会减小,因为避免了较大邻域可能会有大量其他分类的数据点来干扰预测,
然而邻域也不能选择太小,否则一旦出现数据点是噪声(实际应用中肯定存在),预测同样会受到噪声干扰,此时没有足够的正确的数据点来帮助预测分类。
综上算法就是,计算训练数据集中每个数据点与需要预测的数据点的距离,并找出距离最小的k个数据点,然后将这k个数据点归类,数量最多的那个分类就是预测的数据点分类
然而,由于实际中给定的训练数据集可能比较大,这样每次预测一个数据点时,都要经过上面的过程计算,会耗费很长时间,所以需要想方设法提高计算效率,一个常见的方法如下介绍。
kd树(k-dimensional tree)是一种空间切分的数据结构,是一种特殊二叉树,很奇怪的是,k维到底是什么含义?唔,我也没有去想搞清楚它,但显然不是指k近邻法中的k,也不是指数据点的维度n,
我这里就把k-d树看成一个整体,名字就要k-d tree, -_-!! 比如使用二维空间的数据集生成2维的k-d tree
kd树应用于多维空间数据的搜索(比如范围搜索和最近邻搜索)。
每个非叶节点可以认为隐式地形成一个切分超平面,将空间分为两部分,位于超平面左侧(假定一个超平面法向量,左侧可以认为是法向量的反向,那么右侧是法向量的正向)的数据点则构成这个非叶节点的左子树,
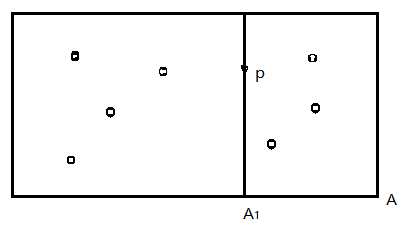
右侧的数据点构成此非叶节点的右子树。超平面的方法这样选择:每个树中节点关联这k维中的一维,对应的超平面垂直于这个维度的轴。举个例子,假设某个超平面经过点p垂直切分某个轴"A"(对应某个维度),切点为A1,
那么在这个维度上,值小于A1的数据点位于这个超平面左侧,而大于A1的数据点位于超平面右侧,如下图就是p有一个共4节点的左子树,有一个共3节点的右子树。另外,为了使生成的二叉树平衡,选择一个节点来形成
切分超平面时,尽量从当前剩余的数据点中使用在某维度上具有中值或者接近中值的数据点
输入:数据集 T = {x1, x2, ... , xN}, y忽略不写,其中x是n维向量
输出:n维 kd树
步骤如下:
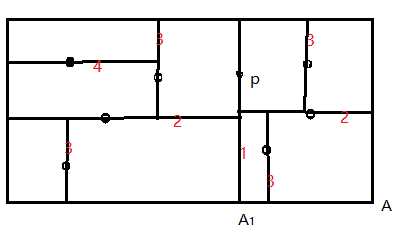
如下图,所示,图中数字表明步骤
先来讨论最近邻搜索
输入:kd树,目标点x,假设维度为n
输出:x的最近邻
步骤:
总结一下,用更简洁的语言描述为:
最后,给出kd树相关的代码说明,注意,代码未经测试,不保证一定能运行,且代码书写简便,未考虑性能优化,仅帮助理解kd树构建和查询过程
public class Point { /// <summary> /// 数据点的实数空间特征向量 /// </summary> public double[] vector; public Point(double[] vector) { this.vector = vector; } /// <summary> /// 计算两个点之间的欧式距离 /// </summary> /// <param name="other"></param> /// <returns></returns> public double Distance(Point other) { if (this.vector.Length != other.vector.Length) throw new Exception(""); double squareSum = 0; for(int i = 0; i < vector.Length; i++) { squareSum += Math.Pow((vector[i] - other.vector[i]), 2); } return Math.Sqrt(squareSum); } public bool EqualsTo(Point other) { if (vector.Length != other.vector.Length) return false; for(int i = 0; i < vector.Length; i++) { if (vector[i] != other.vector[i]) return false; } return true; } } public class Range { public double[,] boundaries; public static Range CreateInf(int dim) { var r = new Range(dim); for(int i = 0; i < dim; i++) { r.boundaries[i, 0] = double.MinValue; r.boundaries[i, 1] = double.MaxValue; } return r; } public Range(int dim) { boundaries = new double[dim,2]; } public Range(double[,] boundaries) { this.boundaries = boundaries; } public Range Intersect(Range r) { if (r.boundaries.Length != this.boundaries.Length) throw new Exception(""); var range = new Range(this.boundaries.Length); for(int i = 0; i < this.boundaries.Length; i++) { var leftMax = this.boundaries[i,0] > r.boundaries[i,0] ? this.boundaries[i, 0] : r.boundaries[i, 0]; var rightMin = this.boundaries[i, 1] < r.boundaries[i, 1] ? this.boundaries[i, 1] : r.boundaries[i, 1]; range.boundaries[i, 0] = leftMax; range.boundaries[i, 1] = rightMin; } return range; } /// <summary> /// 经过点并垂直于坐标轴切割空间,并获取左侧(轴上较小值)空间 /// </summary> /// <param name="p"></param> /// <param name="axis">轴标号,从0开始</param> /// <returns></returns> public static Range LeftRange(Point p, int axis) { if (axis >= p.vector.Length) throw new Exception(""); var range = CreateInf(p.vector.Length); range.boundaries[axis, 1] = p.vector[axis]; return range; } public static Range RightRange(Point p, int axis) { if (axis >= p.vector.Length) throw new Exception(""); var range = CreateInf(p.vector.Length); range.boundaries[axis, 0] = p.vector[axis]; return range; } } public class TreeNode { /// <summary> /// related point /// </summary> public Point point; /// <summary> /// perpendicular on which axis the splitted hyperplane is /// </summary> public int axis; public TreeNode parent; public TreeNode left; public TreeNode right; public Range range; public bool isVisited; public bool isLeftVisited; } public class KDTree { /// <summary> /// root of this K-D tree /// </summary> public TreeNode root; /// <summary> /// dimension /// </summary> public int dim; /// <summary> /// Constructor according to a given list of trainning points /// </summary> /// <param name="points"></param> public KDTree(List<Point> points) { dim = points[0].vector.Length; root = new TreeNode() { range = Range.CreateInf(dim) }; RecursivelyConstruct(root, points, 0); } /// <summary> /// 递归构造K-D树,直到所有数据点被分配完成 /// </summary> /// <param name="node">当前需要确定对应哪个数据点的节点</param> /// <param name="points">当前未分配的数据点</param> /// <param name="depth">当前节点的深度(root为0)</param> private void RecursivelyConstruct(TreeNode node, List<Point> points, int depth) { if(points.Count == 1) { node.point = points[0]; return; } var axis = GetAxis4SplitByVar(points); var m = GetMedianIndex(points, axis); node.axis = axis; node.point = points[m]; if (m > 0) // has left subregion { var t = CreateChildNode(node, true, m, axis, points); RecursivelyConstruct(t.Item1, t.Item2, depth + 1); } if(m < points.Count - 1) // has right subregion { var t = CreateChildNode(node, false, m, axis, points); RecursivelyConstruct(t.Item1, t.Item2, depth + 1); } } /// <summary> /// 搜索与给定点最近的点 /// </summary> /// <param name="p"></param> /// <returns></returns> public Point SearchNearestNode(Point p) { var stack = new Stack<TreeNode>(); // to store those visited nodes DownRecurseSearch(p, root, stack); var leaf = stack.Pop(); var node = Traceback(p, leaf, stack); return node.point; } /// <summary> /// 向下递归访问节点直到遇到叶节点 /// 考虑了某一个子节点为空的情况 /// </summary> /// <param name="p"></param> /// <param name="n"></param> /// <param name="stack"></param> private void DownRecurseSearch(Point p, TreeNode n, Stack<TreeNode> stack) { stack.Push(n); n.isVisited = true; if (n.left == null && n.right == null) return; // leaf reached if (GoDownLeftFirst(p, n)) // go down left as soon as posssible { if(n.left != null && !n.left.isVisited) DownRecurseSearch(p, n.left, stack); else if(n.right != null && !n.right.isVisited) DownRecurseSearch(p, n.right, stack); } else // go down right as soon as posssible { if (n.left != null && !n.left.isVisited) DownRecurseSearch(p, n.left, stack); else if (n.right != null && !n.right.isVisited) DownRecurseSearch(p, n.right, stack); } } /// <summary> /// 继续向下访问节点的子节点,true -> left child node; false -> right child node /// </summary> /// <param name="p"></param> /// <param name="n"></param> /// <returns></returns> private bool GoDownLeftFirst(Point p, TreeNode n) { var axis = n.axis; return p.vector[axis] < n.point.vector[axis]; } /// <summary> /// 向上回溯查找最近邻点 /// </summary> /// <param name="p">目标点</param> /// <param name="n">当前最近邻点</param> /// <param name="stack">已访问过的节点</param> /// <returns></returns> private TreeNode Traceback(Point p, TreeNode n, Stack<TreeNode> stack) { if (stack.Count == 0) return n; var parent = stack.Pop(); // parent node of the current node n // check current node and its parent which is nearer to destination p? var dn = p.Distance(n.point); // distance between n and p, and let it be the currently nearest distance var dp = p.Distance(parent.point); // distance between parent and p if (dp < dn) { dn = dp; // update the currently nearest distance n = parent; // update the currently nearest node } if (Intersect(p, dn, parent)) // 如果p为球心,当前最短距离为半径的超球体与父节点的切割超平明相交,则有必要去父节点的另一个空间向下递归查找最近邻点 { // 当前父节点的另一个子空间,考虑了另一个子空间可能不存在数据点的情况 TreeNode other = null; if (parent.left != null && !parent.left.isVisited) other = parent.left; else if (parent.right != null && !parent.right.isVisited) other = parent.right; if(other != null) { var localStack = new Stack<TreeNode>(); DownRecurseSearch(p, other, localStack); var localNode = Traceback(p, localStack.Pop(), localStack); // get the nearest node in this local sub region // update the min distance and nearest node if needed var localDist = p.Distance(localNode.point); if(localDist < dn) { dn = localDist; n = localNode; } } } // go on up-traceback return Traceback(p, n, stack); } /// <summary> /// 以p为球心,radis为半径的超球体,是否与经过点n且与垂直于n的axis的超平面(切割超平面)相交 /// </summary> /// <param name="p">目标点</param> /// <param name="radis">当前的最近距离</param> /// <param name="n">被考察的节点</param> /// <returns></returns> private bool Intersect(Point p, double radis, TreeNode n) { var axis = n.axis; return Math.Abs(p.vector[axis] - n.point.vector[axis]) < radis; } /// <summary> /// 创建子节点 /// </summary> /// <param name="parent">父节点</param> /// <param name="isLeft">是否为左子节点</param> /// <param name="m">父节点对应空间的数据集中位数索引</param> /// <param name="axis">作用维度</param> /// <param name="points">父节点对应空间的数据集</param> /// <returns></returns> private Tuple<TreeNode, List<Point>> CreateChildNode(TreeNode parent, bool isLeft, int m, int axis, List<Point> points) { var subRegion = isLeft ? points.Take(m).ToList() : points.Skip(m + 1).ToList(); var node = new TreeNode(); node.parent = node; var range = isLeft ? Range.LeftRange(points[m], axis) : Range.RightRange(points[m], axis); node.range = parent.range.Intersect(range); if (isLeft) parent.left = node; else parent.right = node; return new Tuple<TreeNode, List<Point>>(node, subRegion); } /// <summary> /// 选择方差最大的那个维度 /// </summary> /// <param name="points"></param> /// <returns></returns> private int GetAxis4SplitByVar(List<Point> points) { var dim = points[0].vector.Length; var aves = new double[dim]; double max = 0; int axis = 0; for(int i = 0; i < dim; i++) { aves[i] = points.Sum(p => p.vector[i]) / dim; var variance = points.Sum(p => Math.Pow((p.vector[i] - aves[i]), 2)) / dim; if (max < variance) { max = variance; axis = i; } } return axis; } /// <summary> /// 根据深度,轮选维度 /// </summary> /// <param name="depth"></param> /// <param name="dim"></param> /// <returns></returns> private int GetAxis4SplitByDep(int depth, int dim) => depth % dim; /// <summary> /// Given a list of points and the concerned axis, get the index at which the point has a median on the concerned axis /// </summary> /// <param name="points"></param> /// <param name="axis"></param> /// <returns></returns> private int GetMedianIndex(List<Point> points, int axis) { QuickSort(points, 0, points.Count - 1, axis); return points.Count / 2; } private void QuickSort(List<Point> points, int start, int end, int axis) { if(start < end) { int s = start; int e = end; var pivot_i = (start + end) / 2; var pivot_v = points[pivot_i].vector[axis]; while (s < e) { while (s < e && points[s].vector[axis] <= pivot_v) { s++; } while (e > s && points[e].vector[axis] >= pivot_v) { e--; } if (s < e) { var temp = points[s]; points[s] = points[e]; points[e--] = temp; } } QuickSort(points, start, s - 1, axis); QuickSort(points, s + 1, end, axis); } } }
标签:class 分配 部分 适用于 ica rest [] 为我 实际应用
原文地址:http://www.cnblogs.com/sjjsxl/p/6844091.html