标签:位置 .com 邻接表 空间 图的存储 情况 可见 ima node
------------------siwuxie095
图的存储结构
这里介绍 图的存储结构,也称为 图的表示法
毕竟,图画出来并不是为了好玩,而是要用这些图去一些实际问题,
那么要让这些图去解决实际问题,该怎么利用它呢?
第一步,就必须要把 图 变成 数据,而这些数据又能真实的反映出图
中的 顶点与边 或 顶点与弧 之间的关系(这里介绍的也正是第一步)
· 对于有向图来说,它是由 顶点和弧 组成的
· 对于无向图来说,它是由 顶点和边 组成的
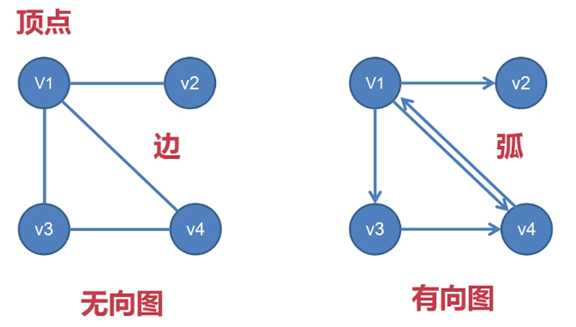
所以,去存储有向图和无向图时,在存储算法上,会有一定的差别
关于图的存储算法,有 4 种比较常用,其中包括 邻接矩阵、邻接表、
十字链表 和 邻接多重表
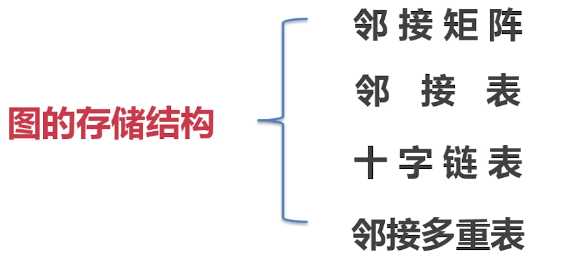
· 邻接矩阵:采用数组进行存储,用来记录 有向图 和 无向图
· 邻接表:采用链表进行存储,用来记录 有向图
· 十字链表:采用链表进行存储,用来记录 有向图
· 邻接多重表:采用链表进行存储,用来记录 无向图
不论是什么样的存储方式,它都是要去存储 顶点与边 或 顶点与弧 的
在介绍这 4 种存储结构之前,先要明晰三个重要概念:弧尾、弧头 和 权值
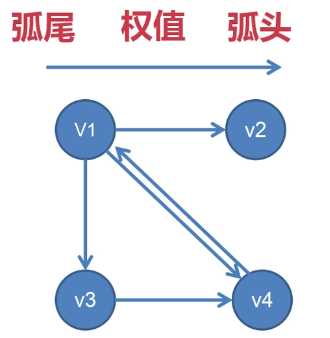
对于上图中的箭头来说:
箭头的尾端(起端) 叫 弧尾,箭头的头端(终端) 叫 弧头
而对于一张图来说:
箭头本身就表示从某一顶点到达某一顶点,则箭头本身有 权值
如:一个城市到另一个城市的道路是 300 公里,就可以把权值
记为 300
总之,权值 是一个抽象的数据,它用来表示 弧 或 边 上的数据,
从而能够为后续的算法提供算法依据
邻接矩阵
邻接矩阵,它采用数组存储,用来记录 有向图 和 无向图

1)对于有向图:

有向图的顶点表达起来很简单,只需存储 顶点索引 和 顶点数据
「顶点索引 - 不可重复」
而弧的表示方法就用到了邻接矩阵
显然,第一种算法的重点在于 邻接矩阵,也就是 弧的表示算法 上
如下:
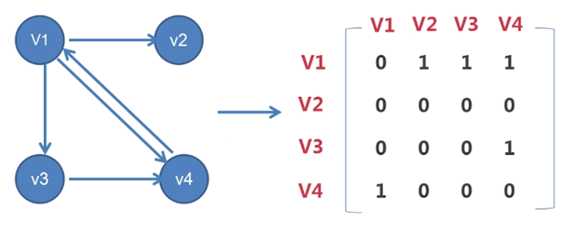
有向图中有四个顶点 v1、v2、v3、v4,把顶点之间的弧,用 1 表示,
而没有弧的地方,用 0 表示
于是,可以将 v1 到 v4 这四个顶点在矩阵当中分别列开
显然,v1 和 v1 本身是不可以到达的,就写上 0,而 v2 和 v2、v3 和 v3、
v4 和 v4,同理 … 都写上 0,所以主对角线上都是 0
除了自身不能到达自身之外,自身到达其他顶点的情况,如下:
v1 到 v2、v3、v4 各有一条弧,所以把 v1 到 v2、v1 到 v3、
v1 到 v4 都记为 1
v2 到 v1、v3、v4 都没有相应的弧,所以把 v2 到 v1、v2 到 v3、
v2 到 v4 都记为 0
v3 只有到 v4 的弧,而没有到 v1、v2 的弧,所以把 v3 到 v4 记为 1,
v3 到 v1、v3 到 v2 记为 0
v4 只有到 v1 的弧,而没有到 v2、v3 的弧,所以把 v4 到 v1 记为 1,
v4 到 v2、v4 到 v3 记为 0
如果 v1 到 v2 不仅有弧,还有权值,那么也可以直接记为 权值,而不是 1,
其它 … 同理 …
这就是有向图的邻接矩阵表达法
2)对于无向图:
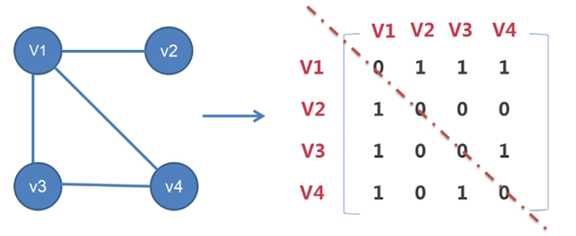
无向图与有向图有着不同:
无向图中,v1 到 v2 与 v2 到 v1 用的是同一条边
所以,v1 到 v2 记为 1,而 v2 到 v1 也记为 1
其它 … 同理 …
不难发现,用邻接矩阵去记录无向图的边时,主对角线的
上方与下方是完全对称的
由此可见,在一个无向图中,记录它的邻接矩阵时,如果
想要节省空间,可以只记录邻接矩阵的上三角部分,或 下
三角部分,这样可以节省一些存储空间
当然,也可以都把它记录下来
那么邻接矩阵如何转换成代码中的语句呢?
可以直接把 邻接矩阵 定义成一个 二维数组 即可,
即 4 行 4 列,然后在相应的位置上用 0、1 来表
达顶点之间的 边 或 弧
「也可以定义为一个 一维数组 …」
通过结构体来表达邻接矩阵,如下:
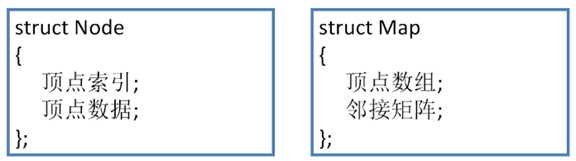
对于图 Map 本身来说,需要存储 顶点数组 和 邻接矩阵
对于顶点 Node 来说,需要存储 顶点索引 和 顶点数据
顶点数组中记录的是所有的顶点,邻接矩阵中记录的是
所有的边,以及顶点与边的关系(或 所有的弧,以及顶
点与弧的关系)
邻接表
邻接表,它采用链式存储,用来记录 有向图

对于有向图:

有向图的顶点需要存储 顶点索引、顶点数据 和 出弧链表头指针
与前面的邻接矩阵相比,多出了一个 出弧链表头指针,那么什么是
出弧链表头指针 呢?
以顶点 v1 为例:
v1 一共有三条出弧,分别指向 v2、v3、v4
v1 的三条出弧形成一个链表,即 出弧链表,而 出弧链表的头结点 即 v1
于是当拿到头节点后,就通过头节点中的出弧链表头指针,依次访问到 v1
的三条弧,而且都是出弧
「注意:头结点没有意义,只起牵头作用」
即 有向图的弧需要表达成 结点,且全部理解为 出弧(相对),它需要存储
弧头顶点索引、下一条弧指针 和 弧数据
以 v1 到 v2 的弧 为例: v2 是弧头,v1 是弧尾
对于 v1 来说, 它上面记录了出弧链表头指针,于是可以通过链表头指针
去找到这条弧,而这条弧又记录了 弧头顶点索引 ,即 v2 的索引
而 v1 到 v2 的弧上记录的 下一条弧指针 和 弧数据,分别是 v1 到 v3 这
条弧的地址 和 v1 到 v2 这条弧的权值
显然,只要有了 顶点的表示方法 和 弧的表示方法,
就能把整个图表达出来,如下:
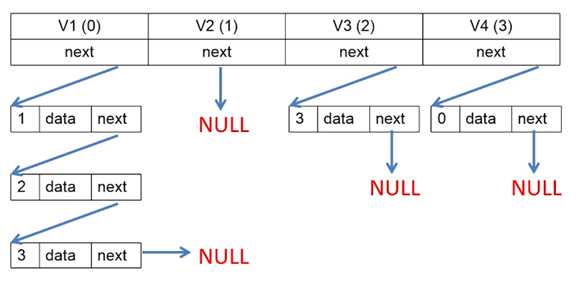
上面一排是四个顶点 v1、v2、v3、v4,假设它们的索引分别是 0、1、2、3
每个顶点下面形成的链表就是 出弧链表,它的结点分为:头结点 和 弧结点
头结点 即 当前顶点,它没有任何意义,只起牵头作用,便于寻址,
其中的 next 即为出弧链表头指针
弧结点 即 当前顶点的所有出弧,其中的 next 为下一条弧指针,
data 为弧的权值,而最前面的即为弧头顶点索引
对于 v1 来说,它的 next 指向 v1 到 v2 的弧,这条弧上有 v2 的索引 1,
同时,这条弧的 next 指向 v1 到 v3 的弧 … 最后一条弧的 next 一定要
指向 NULL
对于 v2 来说,它没有任何一条出弧,所以它的 next 直接指向 NULL
对于 v3 来说,同理 …
对于 v4 来说,同理 …
逆邻接表
与邻接表相对应的概念,叫做 逆邻接表

所谓 逆邻接表,是相对于 邻接表 来说的,二者的区别在于:
1)邻接表的顶点中记录的是出弧链表头指针:
它指向的是 当前顶点 和 当前顶点的出弧 所形成的出弧链表,
出弧链表的弧结点中记录的是 弧头顶点索引
2)逆邻接表的顶点中记录的是入弧链表头指针:
它指向的是 当前顶点 和 当前顶点的入弧 所形成的入弧链表,
入弧链表的弧结点中记录的是 弧尾顶点索引
之所以要改成 弧尾顶点索引,是因为顶点中的记录的是入弧
链表头指针,对于一个弧来说,相当于它的弧头已经确定了,
则弧中就不需要再记录弧头了,直接记录弧尾即可
所以,逆邻接表 与 邻接表 是相对的
通过结构体来表达邻接表,如下:
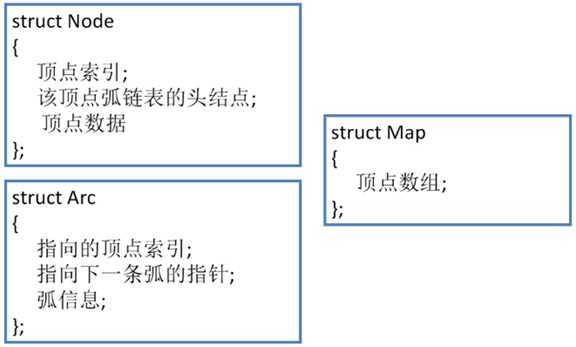
对于图 Map 本身来说,只需要存储 顶点数组 即可
对于顶点 Node 来说,需要存储 顶点索引、顶点数据 和 该顶点弧链表的头结点
该顶点弧链表的头结点 就与该顶点的弧所连接,这条弧又能去找到下一条弧
对于弧 Arc 来说,需要存储 指向的顶点索引、指向下一条弧的指针 和 弧信息
十字链表
十字链表,它采用链式存储,用来记录 有向图

对于有向图:
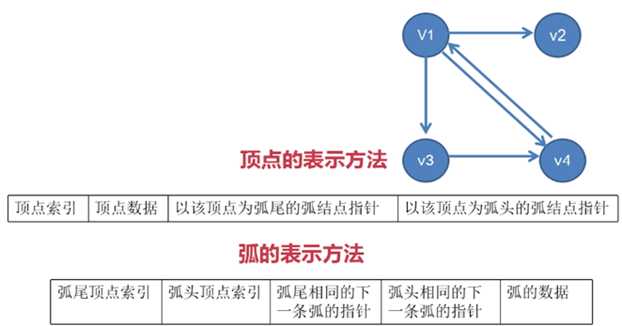
有向图的顶点需要存储 顶点索引、顶点数据、以该顶点为弧尾的弧结点指针
和 以该顶点为弧头的弧结点指针
以 v1 为例:
v1 中要记录的除了 v1 的索引和数据外,还要记录第一条形成的
从 v1 射出去的弧 和 第一条从其它顶点射回来的弧
假设 v1 到 v2 的弧是第一条从 v1 射出去的弧,v4 到 v1 的弧是
第一条从其它顶点射回来的弧,则:
以 v1 为弧尾的弧结点指针就指向 v1 到 v2 的弧,以 v1 为弧头的
弧结点指针就指向 v4 到 v1 的弧
而 有向图的弧则需要存储 弧尾顶点索引、弧头顶点索引、弧数据、
弧尾相同的下一条弧的指针 和 弧头相同的下一条弧的指针
以 v1 到 v2 的弧 为例:
弧尾顶点索引 即 v1,弧头顶点索引 即 v2,弧数据 即 弧的权值
弧尾相同的下一条弧,即 v1 到 v3 的弧 或 v1 到 v4 的弧,如果
该指针指向 v1 到 v3 的弧,则 v1 到 v3 的弧上相应位置的指针
就指向 v1 到 v4 的弧
弧头相同的下一条弧,不存在,所以将该指针置为 NULL
通过结构体来表达十字链表,如下:

对于图 Map 本身来说,只需要存储 顶点数组 即可
对于顶点 Node 来说,需要存储 顶点索引、顶点数据、
第一条入弧节点指针 和 第一条出弧结点指针
其中:第一条入弧 和 出弧 结点指针 的类型正是 弧类型
对于弧 Arc 来说,需要存储 弧尾顶点索引、弧头顶点索引、
指向下一条弧头相同的弧的指针、指向下一条弧尾相同的弧
的指针、以及弧信息
索引可以是字母 char 类型,也可以是数字 int 类型,还可以
是任意一种能够不重复的类型
而指向弧的指针必然就是弧本身的指针,即 Arc 类型
邻接多重表
邻接多重表,它采用链式存储,用来记录 无向图

对于无向图:
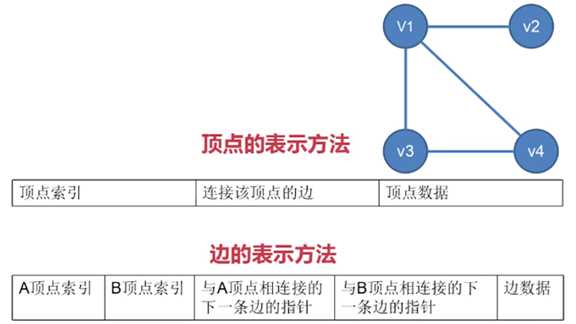
无向图的顶点需要存储 顶点索引、顶点数据 和 连接该顶点的边
以 v1 为例:
v1 中要记录的除了 v1 的索引和数据外,还要记录的边有 3 条,
即 v1 到 v2 的边、v1 到 v3 的边、v1 到 v4 的边
实际上要记录的是指向第一条边的指针,假设 v1 到 v2 的边是
第一条边,则记录指向这条边的指针即可
而无向图的边需要存储 A 顶点索引、B 顶点索引、边数据、
与 A 顶点相连接的下一条边的指针 和 与 B 顶点相连接的
下一条边的指针
以 v1 到 v2 的边 为例:
A 顶点索引 即 v1 的索引,B 顶点索引 即 v2 的索引,边数据 即 边的权值
与 A 顶点相连接的下一条边,与 v1 相连接的下一条边,即 v1 到 v3 的边
或 v1 到 v4 的边,如果该指针指向 v1 到 v3 的边,则 v1 到 v3 的边上相
应位置的指针就指向 v1 到 v4 的边,这取决于哪条边先建立起来的
与 B 顶点相连接的下一条边,即 与 v2 相连接的下一条边,不存在,所以
将该指针置为 NULL
通过结构体来表达邻接多重表,如下:

对于图 Map 本身来说,只需要存储 顶点数组 即可
对于顶点 Node 来说,需要存储 顶点索引、顶点数据 和 第一条边结点指针
第一条边的结点指针就意味着能找到一条边
对于边 Edge 来说,需要存储 顶点 A 的索引、顶点 B 的索引、边信息、
连接 A 的下一条边的指针 和 连接 B 的下一条边的指针
索引可以是字母 char 类型,也可以是数字 int 类型,还可以是任意一种
能够不重复的类型
而连接边的指针必然就是边本身的指针,即 Edge 类型
【made by siwuxie095】
标签:位置 .com 邻接表 空间 图的存储 情况 可见 ima node
原文地址:http://www.cnblogs.com/siwuxie095/p/6849765.html