标签：十字路口 避免 src 关系 专业 under 连通性 线数据 包括
有很多同学虽然成功做好了网络数据集，但是分析时会出现这样的问题：
这是为什么呢？
这有三个可能的原因：
1. 两个点之间所有的道路没有连通（问题出在点、线数据上）。
2. 网络数据集出现了孤立的点位置。
3. 网络数据集的连通性有问题。
我就从这三个方面说说，如何避免这些问题。因为标题起的是点线要素的制作情况，我就着重讲第一点了，后两个情况简单说说，在第四章网络数据集的连通性会详细说。
还分两个简单的情况：
一个是点不在线上；
另一个比较复杂：线之间二维没有由折点连通。
这里的由，用专业的说法就是"via"，或者"by"。
点不在线上很容易，初中数学都说过的，想必证明点在线上的问题已经让各位头疼了吧。
那么，什么是“线之间二维没有由折点连通”？
我们暂时假定道路数据是没有高程数据的，也就是说，所有的道路均在二维平面上。
伟大的数学家华罗庚说过，“数有形时可直观,形有数时能入微”。我们画图吧！
我们知道，ArcGIS里的线是Polyline，一个Polyline数据集有多条折线，一条折线由n个折点（也叫结点、节点、端点）和n-1条线段组成，例如下图：
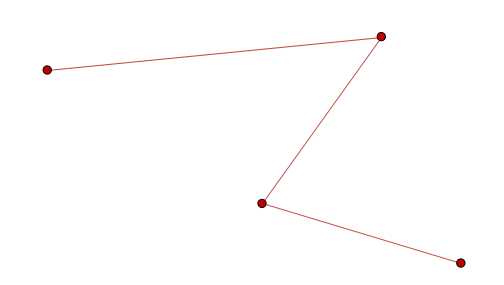
这个三折线就包括了3条线段和4个折点组成。
那么熟悉了折点的概念，我们往下看看，什么是二维间没有折点连通？
我又画了一条三折线，用绿色的折点表示：
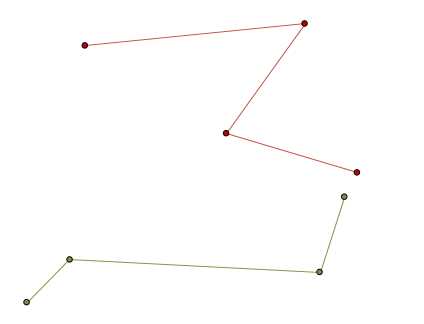
现在，我将绿色的三折线挪动，与红色的线相交，只会有这样的三种情况：
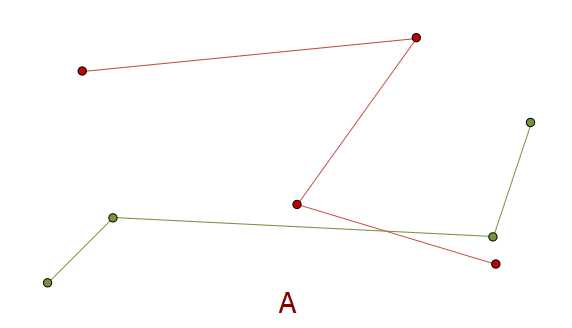
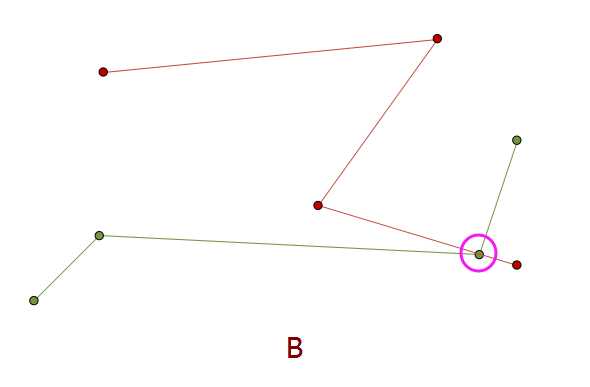
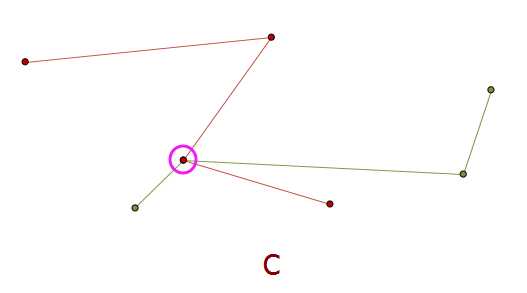
A、B、C三种情况有什么不同？
在ArcGIS中，如果不显示折点，是根本看不出是如何相交的。
A：线相交，但是存在上下的关系
B：线相交，虽然存在上下关系，但是有一条线的一个折点在另一条线的边上
C：线相交，虽然存在上下关系，但是一条线的一个点与另一条线的折点重合
现在我们再来看看“线之间二维没有经过折点连通”，就十分容易了：A、B两个情况均为此情况，只要是这样的情况
构建的网络数据集都不会在线的交点处连通。
——————————那么，说清楚了，如何画线是最科学的呢？——————————
- 十字路口、岔路口处设置折点。
- 立交桥处不设置折点（这样就不连通了）。
- 立交桥的匝道出入口设置折点。
如果涉及立交桥，那么就需要设置高程字段了，而且是涉及了三维线数据的端点连通问题，更为复杂。
在此我暂时不解释，有兴趣的同学可以参考官方的帮助文档，说的很详细。（其实就是画起来和解释起来比较麻烦，篇幅原因，怕读者拍砖看不懂、说我写的复杂，就不继续写了，从我的二维情况可以推广到三维的情况）
说实话，A和B完全就可以看作有一条线在另一条线的上空，你想想，两条路如果不相交，而是上下的关系，车子怎么切换道路呢？当然也就不连通咯。
但是，在二维世界里没有第三个维度，所以看起来“叠合”在一起了而已。
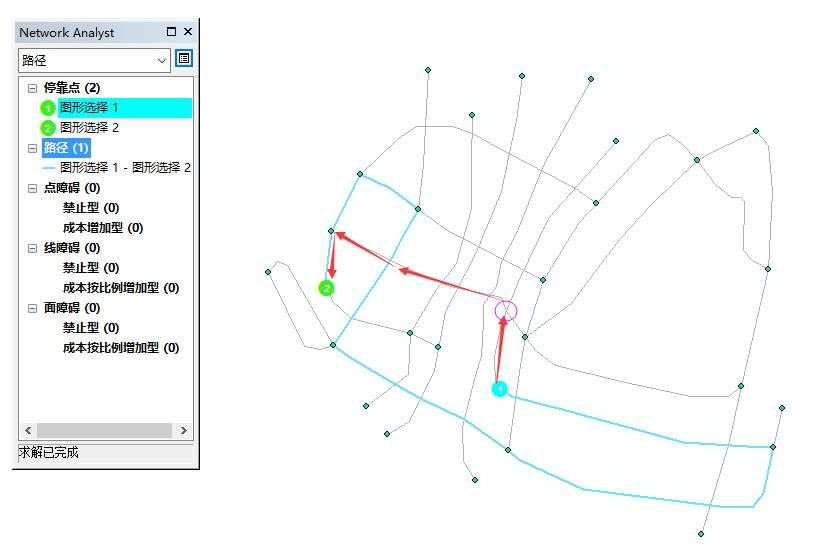
为什么不按红线走呢？
因为紫色圈的地方根本没有“二维按折点连通”。可以看到，蓝色的点即为网络数据集的连通点，紫色圈的地方没有连通的折点，说明相交的两条线确实没有“二维按折点连通”。
见Route.shp编辑下的状态：
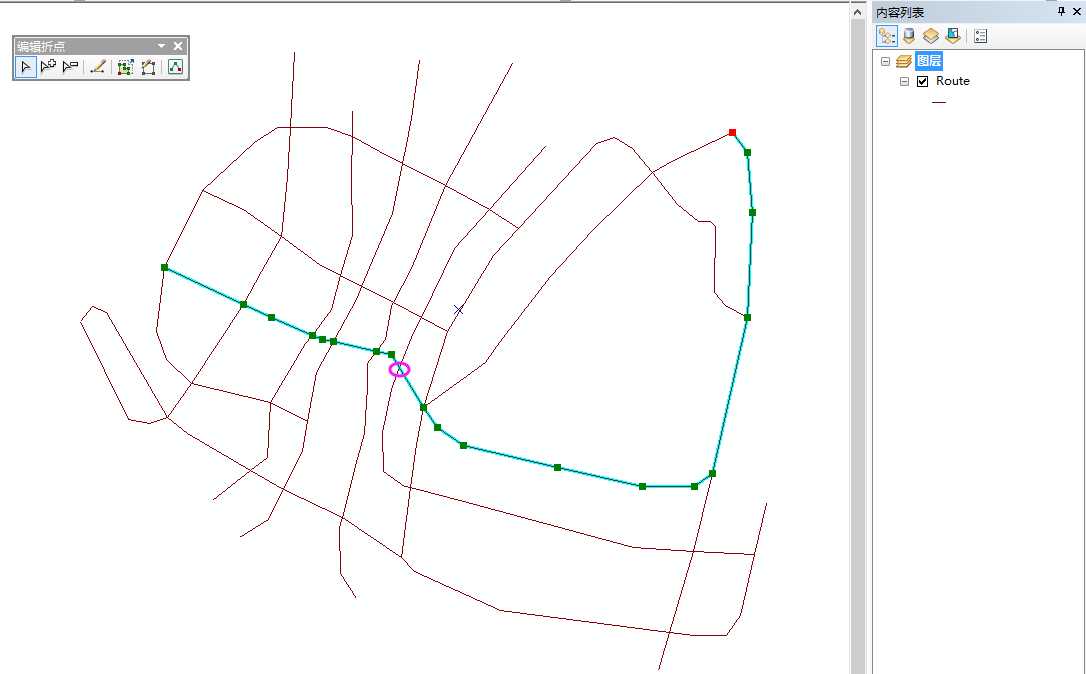
是没有绿色的折点的，难怪不能连通了。
在我的编辑下，Route.shp已经全部实现了每条线交叉的地方都有折点。见新的网络数据集的Junctions：
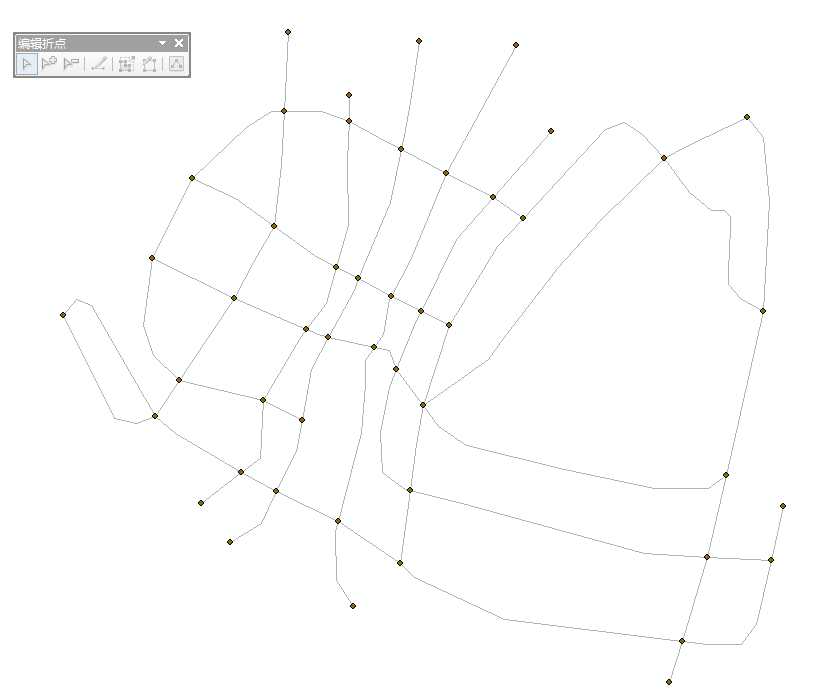
每个交叉点都是连通的，所以道路也就畅通无阻（当然这是假定交点都是十字路口，不是立交桥）
这个点类似于岛屿，其实就是上面提及的点不在线上，构建网络网络数据集的时候就成了孤立的点。
（这个问题一直困扰着我，最近才解决）
还是画图更直观吧！
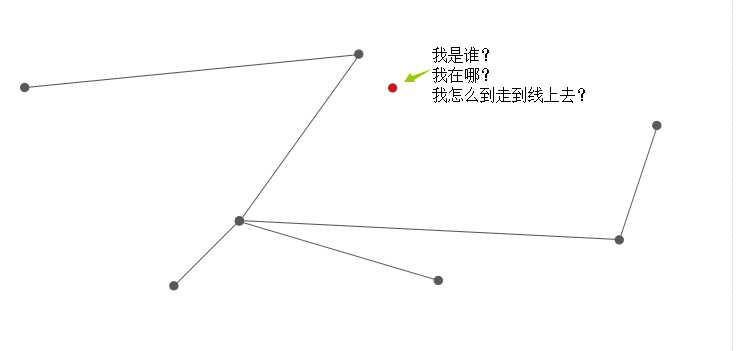
红色的点假设是点要素类中的一个点要素，并不在任何一条线上，虽然可以创建网络数据集，但是在网络数据集中是孤零零的一个点：
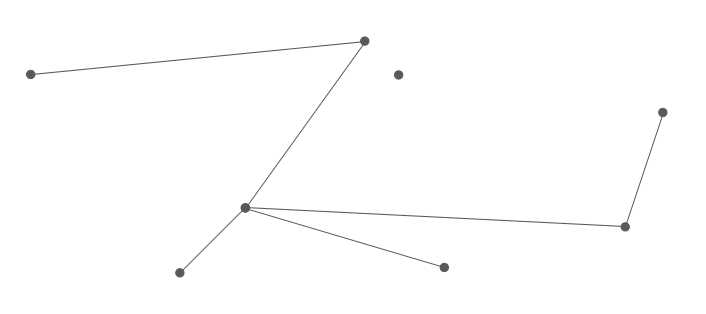
然而，在网络数据集中孤立的点并不会显示，端点也不会显示，例如有这样的一幅网络数据集：
我们是看不到端点的，也看不到孤立的点。上上个图我只是把端点和孤立点“画”了出来。
所以如果存在这样的路网数据和点数据：
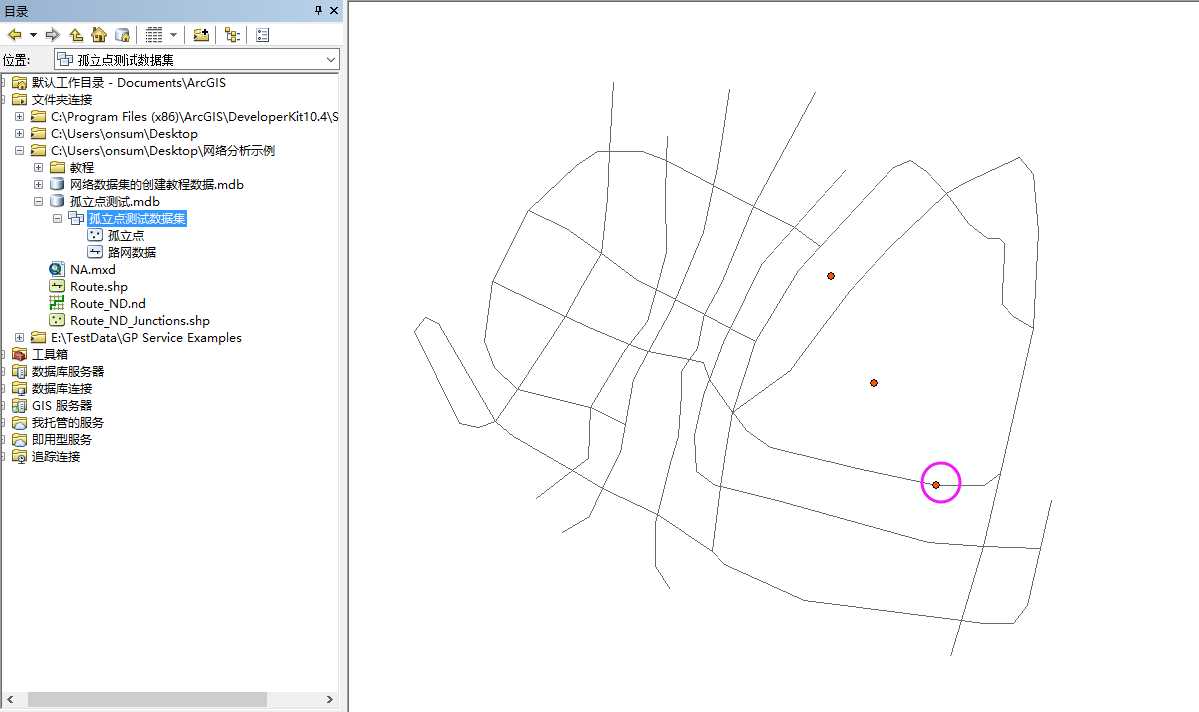
两个点是孤立点，一个点在线的折点上（而不是在线上） （为啥这样说，下一篇会写到如果有点数据，网络数据集又如何创建）
构建网络数据集时，点数据选择依边线连通：
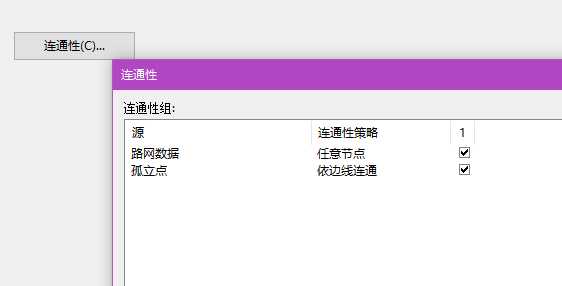
完成时会提示：
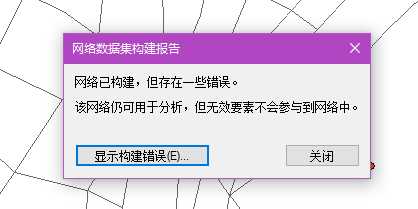
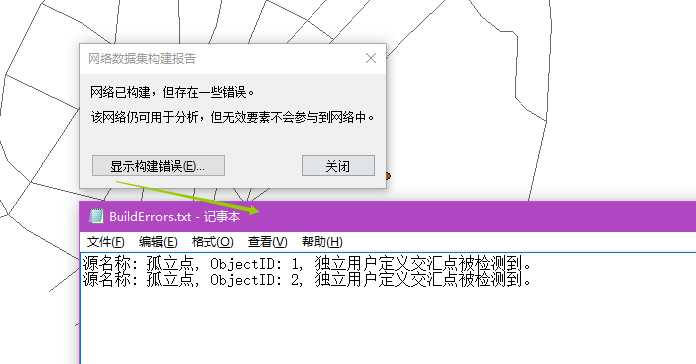
这样就存在了孤立点。
虽然不影响，但是如果精确地添加了网络位置到这些独立的点上，自然就会出现文章开头的无法分析的情况。
网络位置是可以用这个工具添加的：
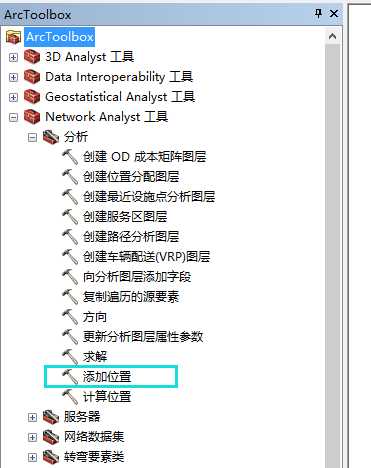可以简单理解网络位置为最短路径中的起点终点，最近设施点等。
当使用构建网络数据集的点要素添加为网络位置点时，就说精确重合了，那当然是不连通的，没法分析咯。
这个属于以后的内容，在这里就不细说了，等以后写完第四章的连通性问题，就会在这里跟进超链接。
ArcGIS 网络分析[1.4] 制作点线要素时需要注意的地方
标签：十字路口 避免 src 关系 专业 under 连通性 线数据 包括
原文地址：http://www.cnblogs.com/onsummer/p/6850520.html
