标签:height 重构 hdfs block 大量 关联分析 其他 资源 选择
一、简单介绍大数据技术产物
“大数据”一词首先出现在2008年9月《Nature》杂志发表的一篇名为“Big Data: Wikiomics”的文章上(Mitch,2008)。“大数据科学”尚未有统一定义,但是科学家普遍认为它是以海量的多元异构数据为主要研究对象,以大数据的存储、处理和理解方法为主要研究内容,以新兴的计算技术为主要研究工具,以扩展人类对数据的利用能力为主要目标的一门新兴的综合性学科。它主要针对当前海量(volume)、多元(variety)和高速更新(velocity)数据的处理问题,重点研究如何将当前高速发展的计算技术用于数据处理/挖掘、有效地利用数据、从海量多元的数据本身去发现新的知识。
在存储上,hdfs的分布式存储可以任意水平扩展,可以解决数据存储的难题。
在计算上,从最初的MapReduce,把任务水平拆分,多台机器并行计算,再汇总结果;
到基于Spark的内存计算,改造Mapreduce每次数据落盘以及编程方式的痛点。
有了存储和计算框架,周边就衍生出了很多管理、缓存相关的技术,比如:
处于大数据时代下的产物:

二、介绍时空大数据
时空大数据定义:越来越多的数据使世界进入真正的大数据(Big Data)时代,其中大量的与时空位置有关的数据称为时空大数据。比如Uber网约车实时车辆位置,外卖配送等等。
时空大数据由于其所在空间的空间实体和空间现象在时间、空间和属性三个方面的固有特征,呈现出多维、语义、时空动态关联的复杂性,因此,需要研究时空大数据多维关联描述的形式化表达、关联关系动态建模与多尺度关联分析方法,时空大数据协同计算与重构提供快速、准确的面向任务的关联约束。具体特点包括:
1)时空大数据包含对象、过程、事件在空间、时间、语义等方面的关联关系。
2)时空大数据具有时变、空变、动态、多维演化特点,这些基于对象、过程、事件的时空变化是可度量的,其变化过程可作为事件来描述,通过对象、过程与事件的关联映射,建立时空大数据的动态关联模型。
3)时空大数据具有尺度特性,可建立时空大数据时空演化关联关系的尺度选择机制;针对不同尺度的时空大数据的时空演化特点,可实现对象、过程、事件关联关系的尺度转换与重建,进而实现时空大数据的多尺度关联分析。
4)时空大数据时空变化具有多类型、多尺度、多维、动态关联特点,对关联约束可进行面向任务的分类分级,建立面向任务的关联约束选择、重构与更新机制,根据关联约束之间的相关性,可建立面向任务的关联约束启发式生成方法。
5)时空大数据具有时间和空间维度上的特点,实时地抽取阶段行为特征,以及参考时空关联约束建立态势模型,实时地觉察,理解和预测导致某特定阶段行为发生的态势。可针对时空大数据事件理解与预测问题,研究空间大数据事件行为的本体建模和规则库构建,为异常事件的模式挖掘和主动预警提供知识保障,可针对相似的行为特征,时空约束和事件级别来挖掘事件模式并构建大尺度事件及其应对方案的规则库。
时空大数据一方面具有一般大数据的大规模、多样性、快变性和价值性的特点,另一方面还具有与对象行为对应的多源异构和复杂性、与事件对应的时/空/尺度/对象动态演化、对事件的感知和预测特性。
目前来看,国际上的时空大数据科学的研究仍处于起步阶段,需要面向具体应用开展深入研究。例如在国防领域,整体态势感知是现代化国防的关键,具有整体获取特性的遥感大数据在国防上意义重大;在气象领域,空间信息是气象预测的基础,能融合时空大数据的气象大数据将为大气环境监测、农业灾害监测提供强有力的支撑;在交通领域,融合了地理位置信息、空间信息的时空大数据将是应急处置的重要决策依据,可以提高应急交通指挥决策的科学性。因此,进一步研究时空大数据表示、度量和理解的基本理论和方法,揭示时空大数据与现实世界对象、行为、事件间的对应规律,将大有可为。
三、介绍时空大数据中的基础操作
1.最近邻查询 (离我最近的人是谁?)
2.反向最近邻查询 (谁的最近邻查询是我?结果为一个集合)
3.范围查询(距离我10m范围内都有谁?)
4.空间集成查询(聚合查询,距离我10m范围内有几个人?)
5.最短路径查询(从沙河到学院路的最短路径)
6.最优选址查询(麦当劳选址问题)
四、介绍索引结构
索引结构R-tree。R-tree结构类似于B树,R-tree是B树在高维空间的扩展,是一棵平衡树。每个R树的叶子结点包含了多个指向不同数据的指针,这些数据可以是存放在硬盘中的,也可以是存在内存中。根据R-tree的这种数据结构,当我们需要进行一个高维空间查询时,我们只需要遍历少数几个叶子结点所包含的指针,查看这些指针指向的数据是否满足要求即可。这种方式使我们不必遍历所有数据即可获得答案,效率显著提高。
举例说明:
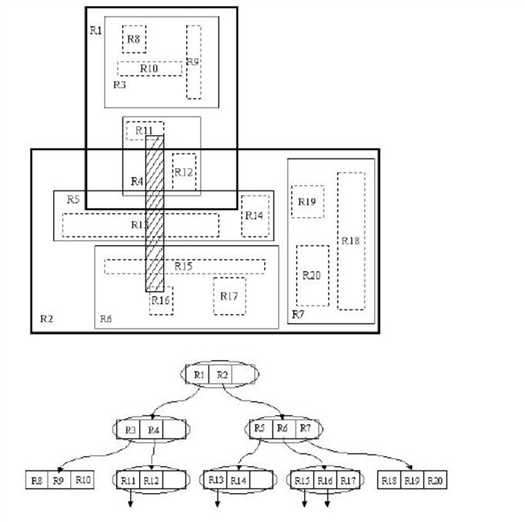
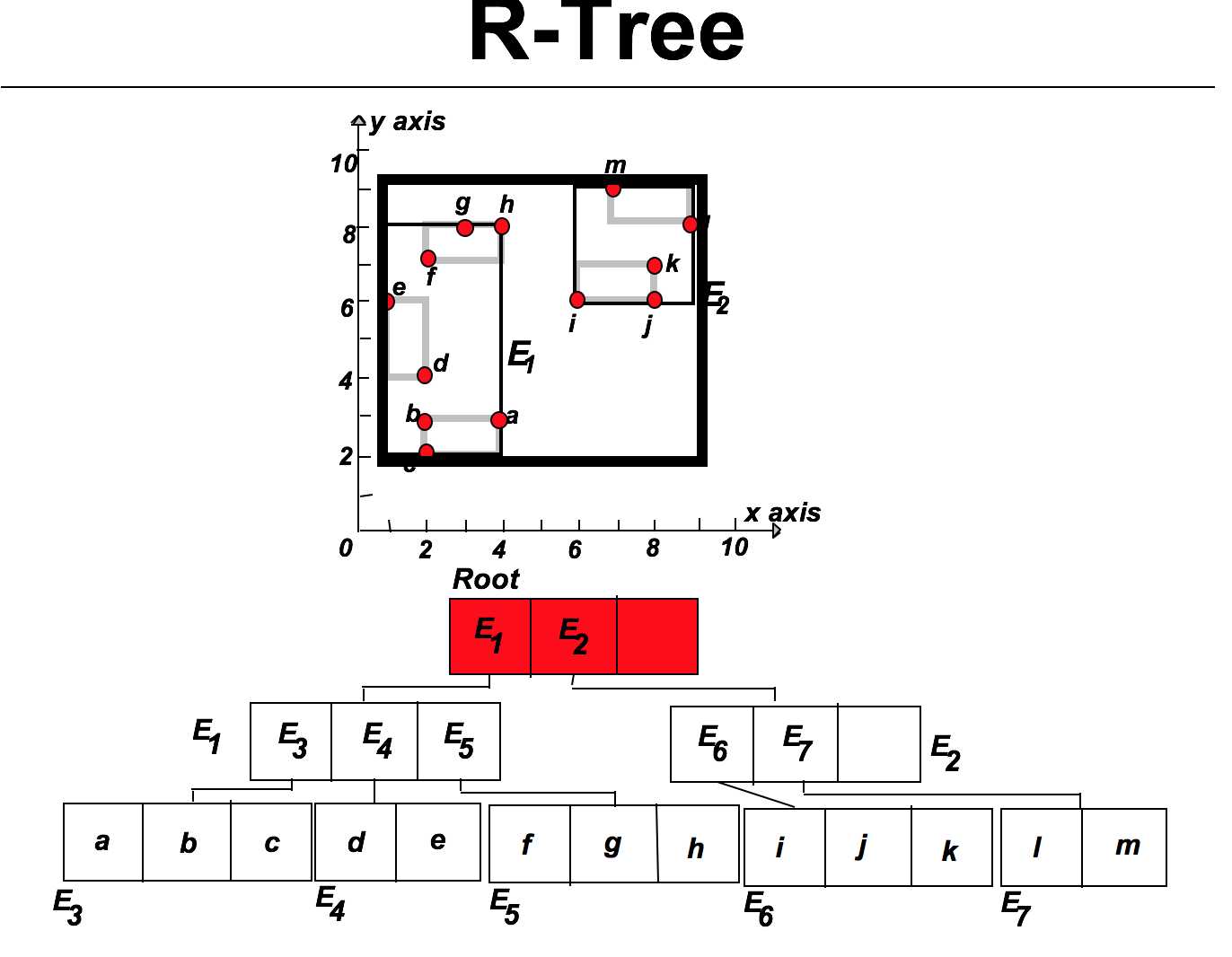
其中的矩形是按照Minimum Bounding Rectangle(MBR)进行划分的。其中每个结点最大的子节点数量d可以自定义,并且在上面的例子里设为d=3。
R-tree的一些特性:
基于磁盘的: 存储在磁盘上,加载需要的部分到内存。
分页的: 每个节点是一个固定大小的磁盘页 (e.g. 8KB)。
平衡的: 所有节点距离根节点的距离相等。
动态的更新: 动态插入/删除。
叶节点存储: 所有的记录都存在叶子节点中。
最小容量: 每个节点(除根节点)数据至少占一半空间。
利用R-tree实现范围查询的过程如下:
从根节点开始:
1.若当前节点是非叶子结点,对该节点的每个子节点<E, ptr>进行如下判断:如果E的MBR和Q有重叠,搜索ptr指向的子树。
2.如果当前节点是叶子节点,则返回叶子节点中位于Q内的点。
下图给出阴影部分为查询范围!很直观可以得到在阴影内的点有b和d,下图解释如何利用R-tree完成这一范围查询操作。
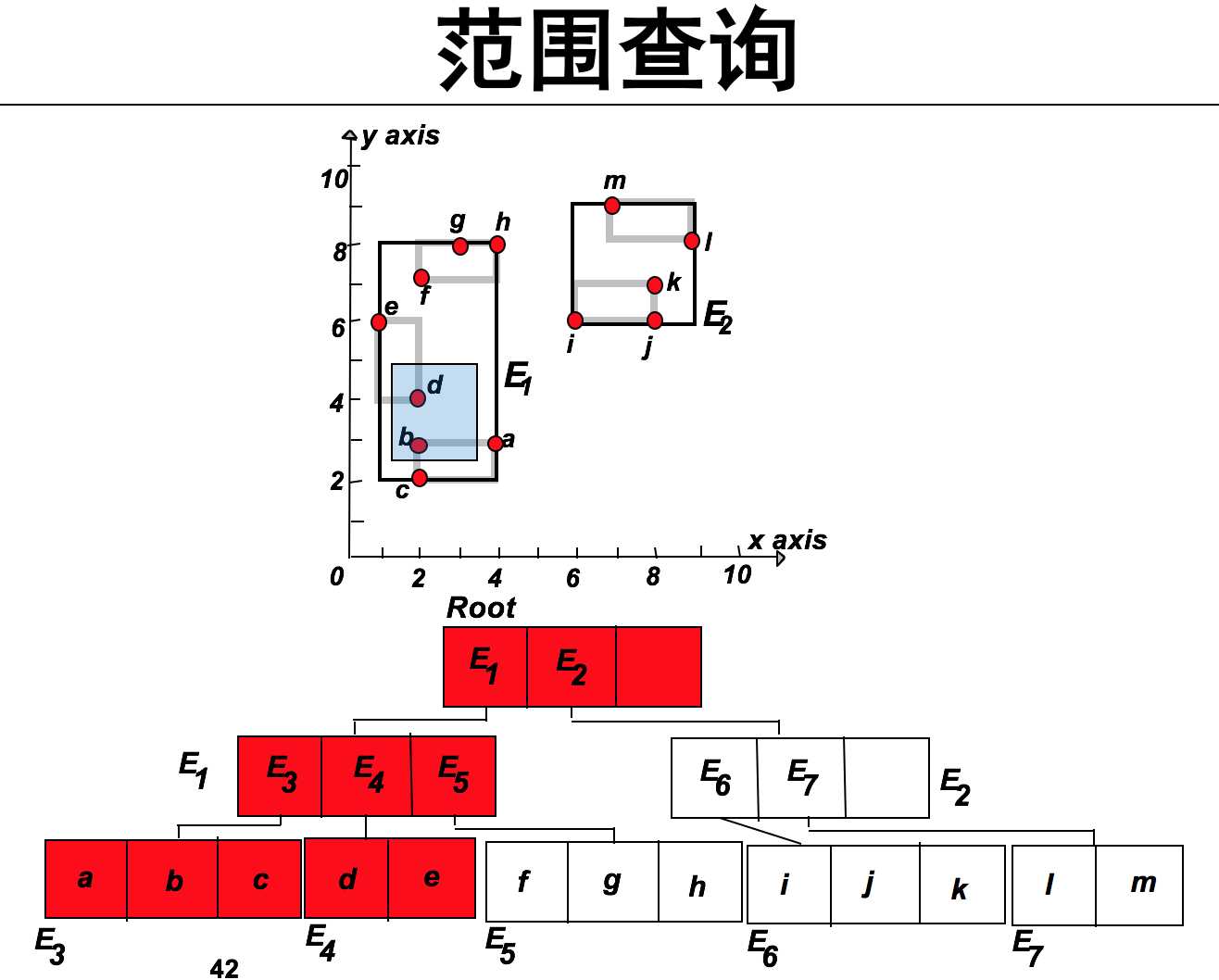
利用R-tree实现聚合查询的过程如下:
求解算法:
直接想法:先转换成范围查询,然后计数。
更好的想法:对每个index实体都保存对应其子树的聚合的值。
保存每个Index实体子树聚合的数量值,如果当前查询完整包括某个MBR,则将求解的ans加上该部分的Index中保存的数量值。实现剪枝操作,注意这里的剪枝是有前提条件以及相应的操作的!!!(前提条件:MBR属于查询范围Q;相应操作 ans+=MBR‘s Index num)
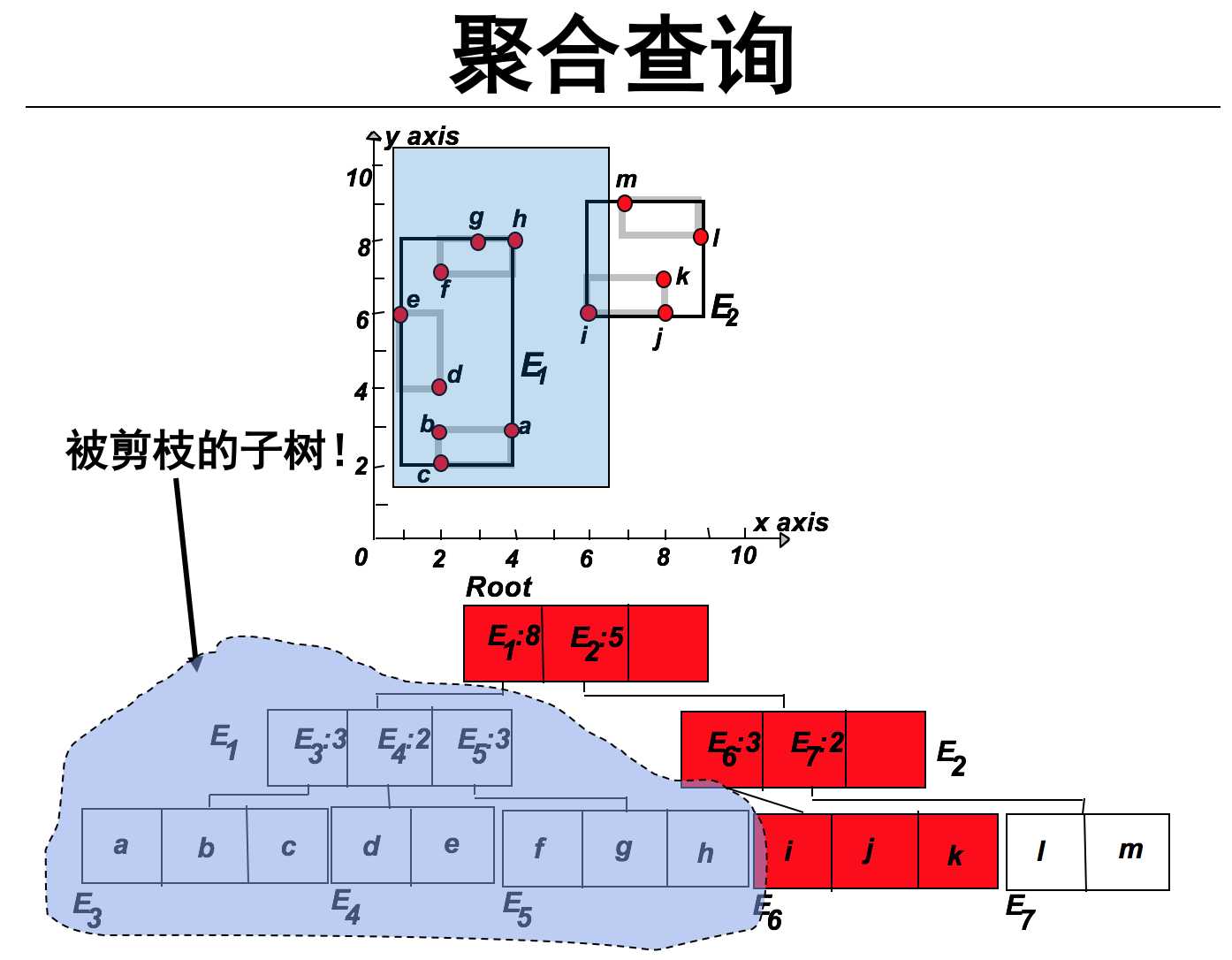
下面简单介绍R-tree的构建:插入对象
从根节点开始向下查找“最适合”的叶子节点L。
1,找到插入该节点需要扩大面积最小的子节点。如果有两个这样的节点,则选择MBR面积较小的节点。
如果该叶子节点L有剩余位置,插入o完成操作。否则,将L分裂为L1和L2。
1,调整L内的对象的范围使L恰覆盖L1。
2,向L的父节点添加一个子节点覆盖L2(可能会引起父节点的递归分裂)。
因此操作可以简化为:
1. 无分裂、无扩大区域
2. 无分裂、需扩大区域
3. 需要分裂
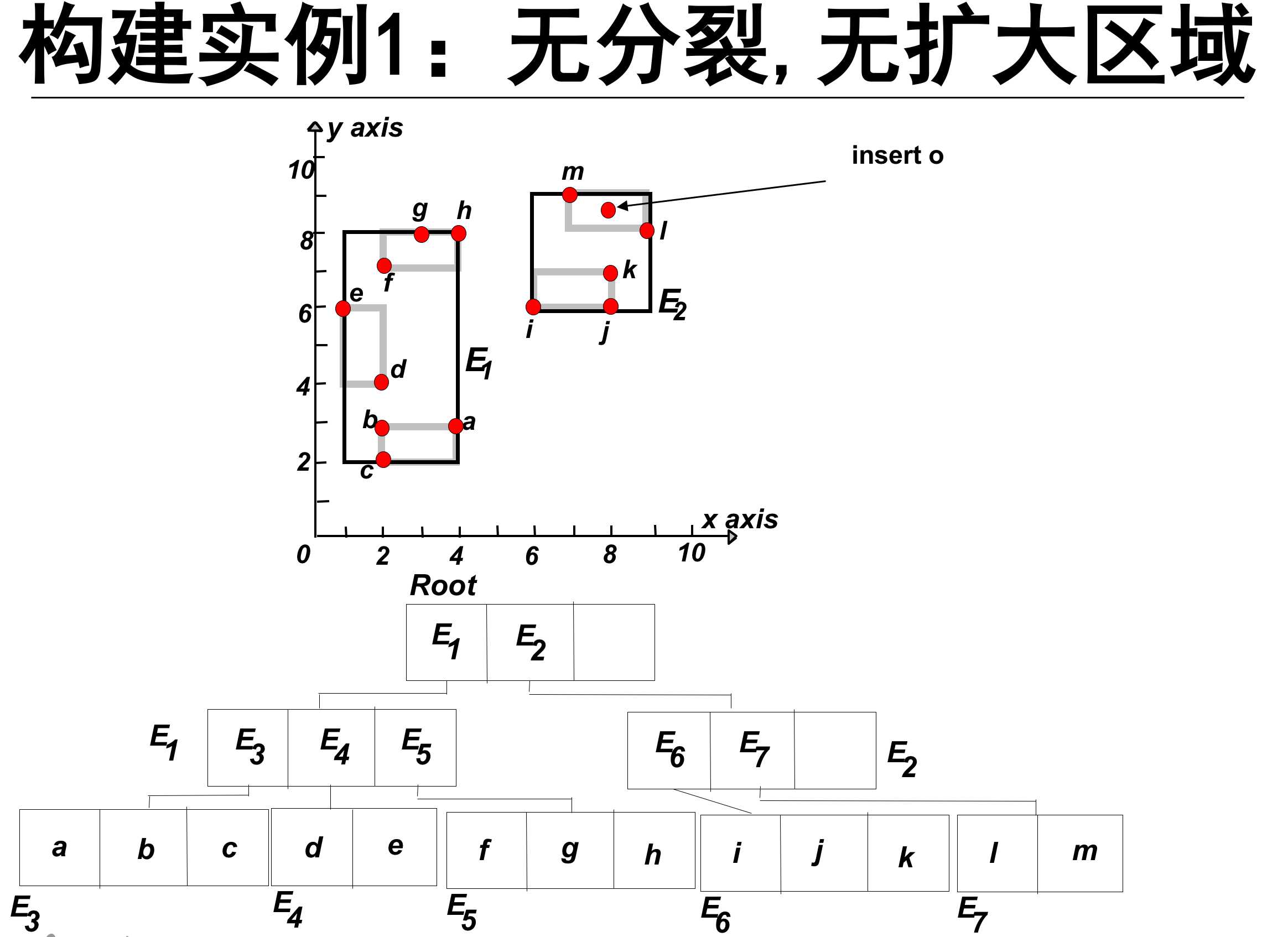
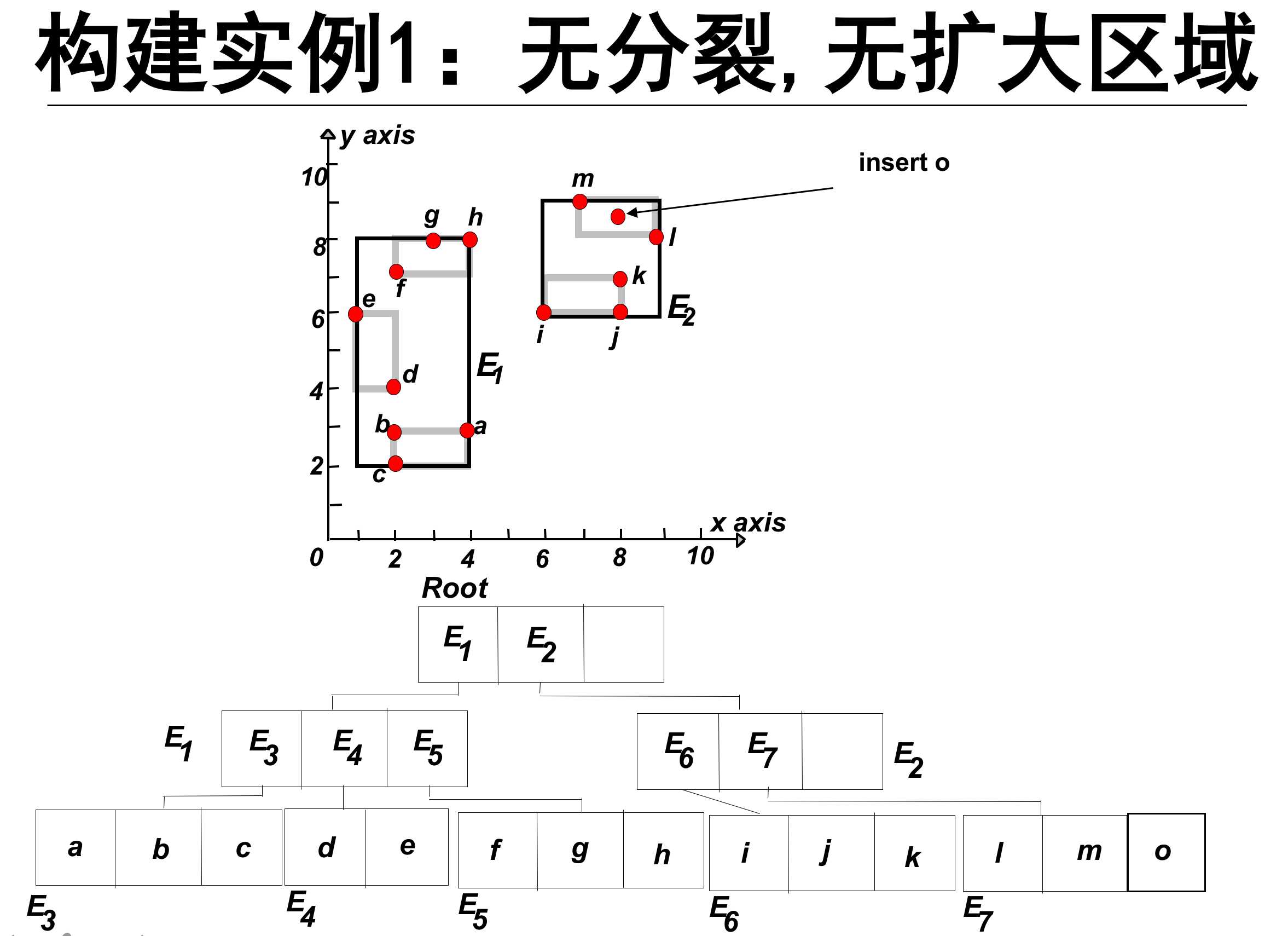
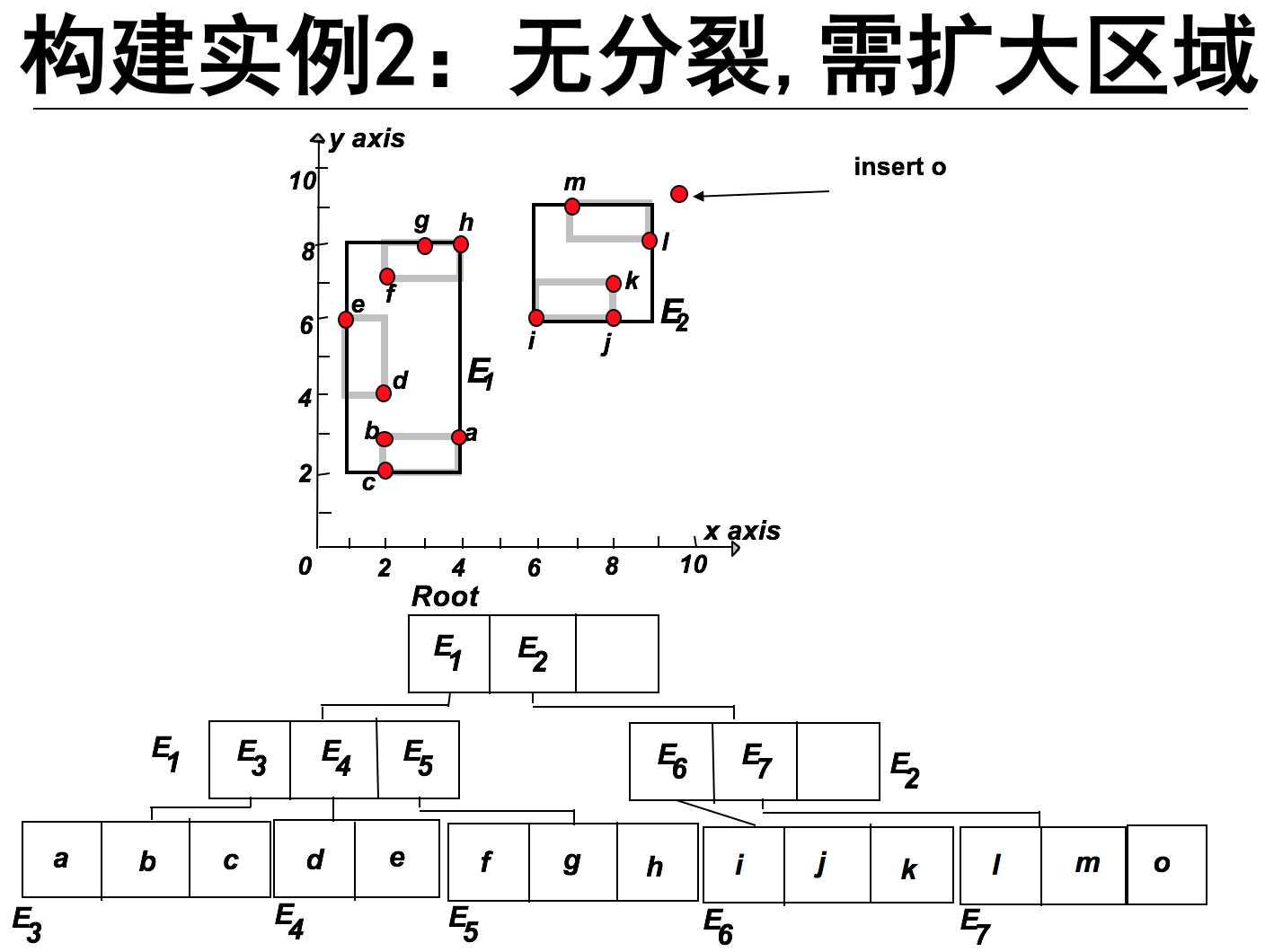
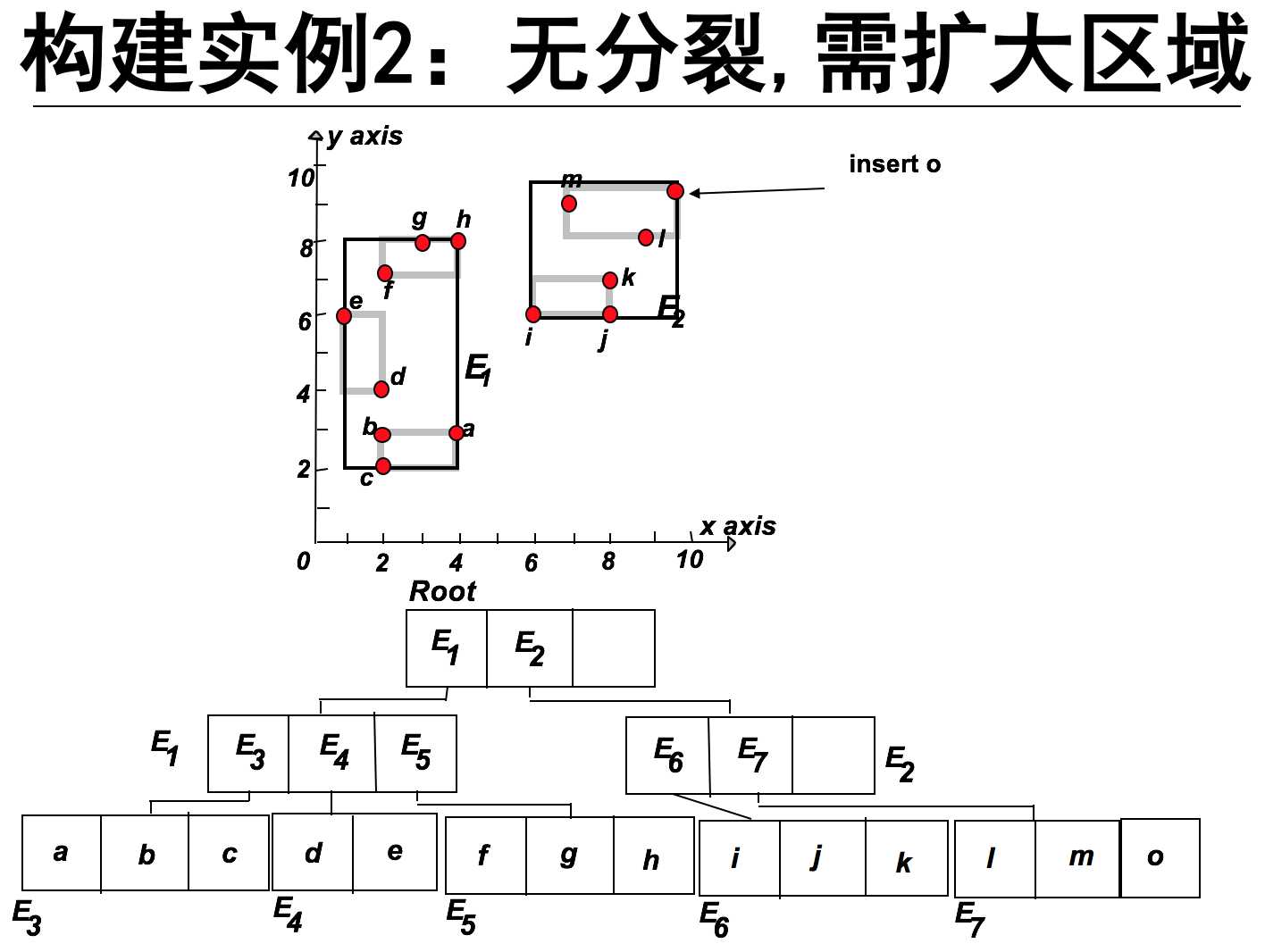
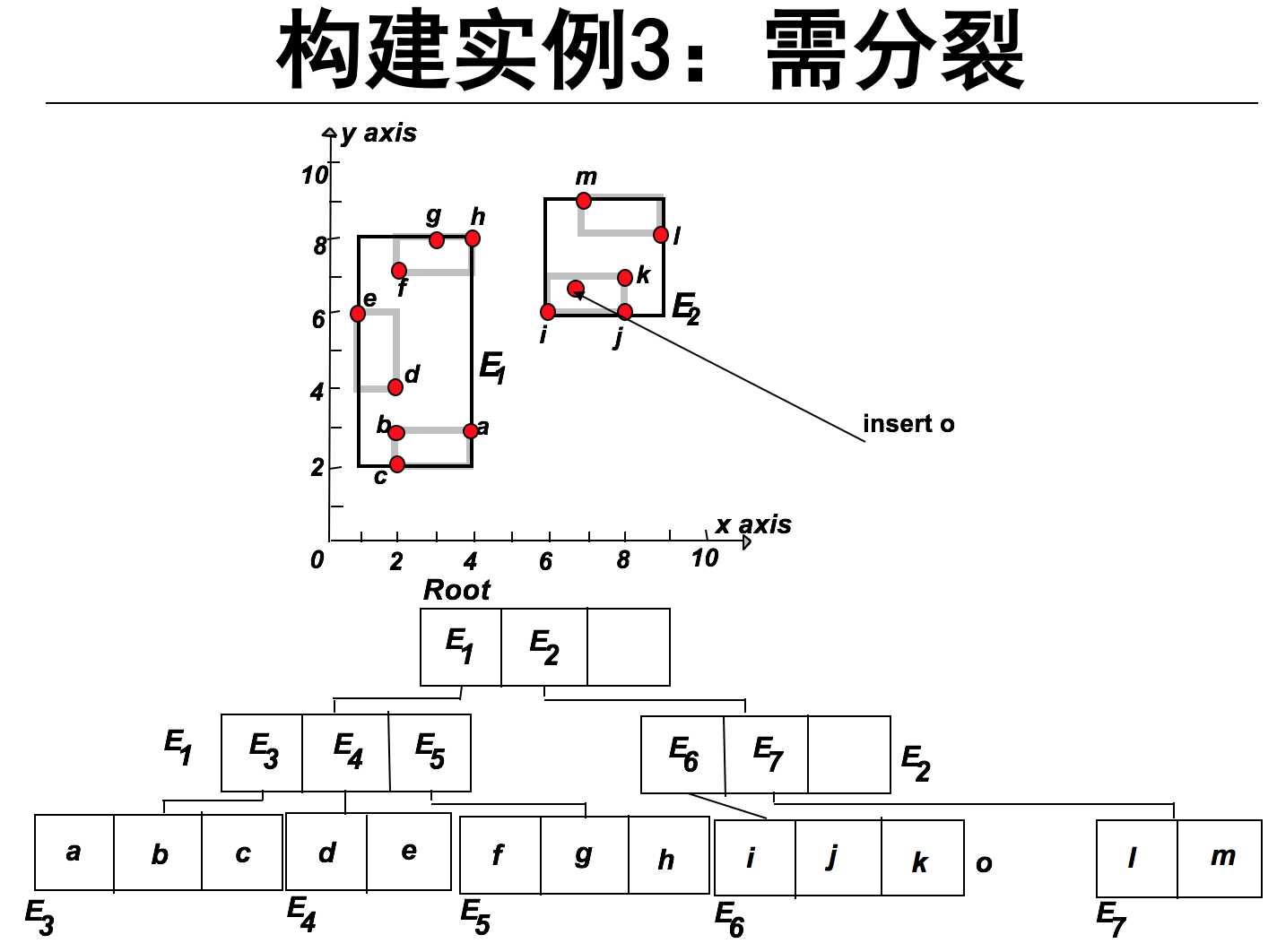
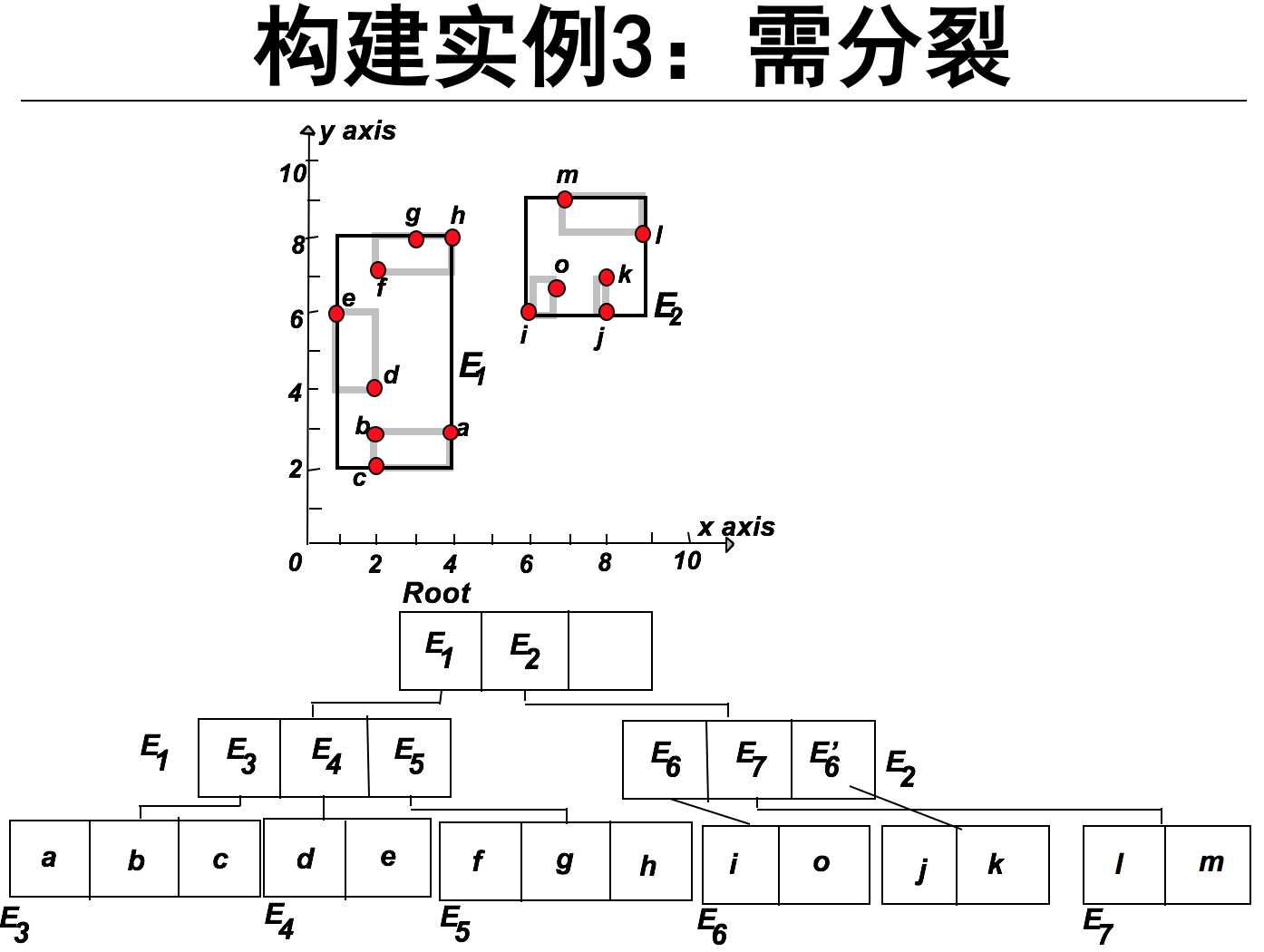
L中原有的对象和新插入的实体必须位于L1或L2中。目标是减少L1和L2覆盖区域在随后查询中的重叠程度。思路:以最小化面积为目标重新分配L1和L2的区域。
1. 穷举算法速度慢;
2.可以在平方或者线性时间下获得近似结果。
最近邻查询操作:


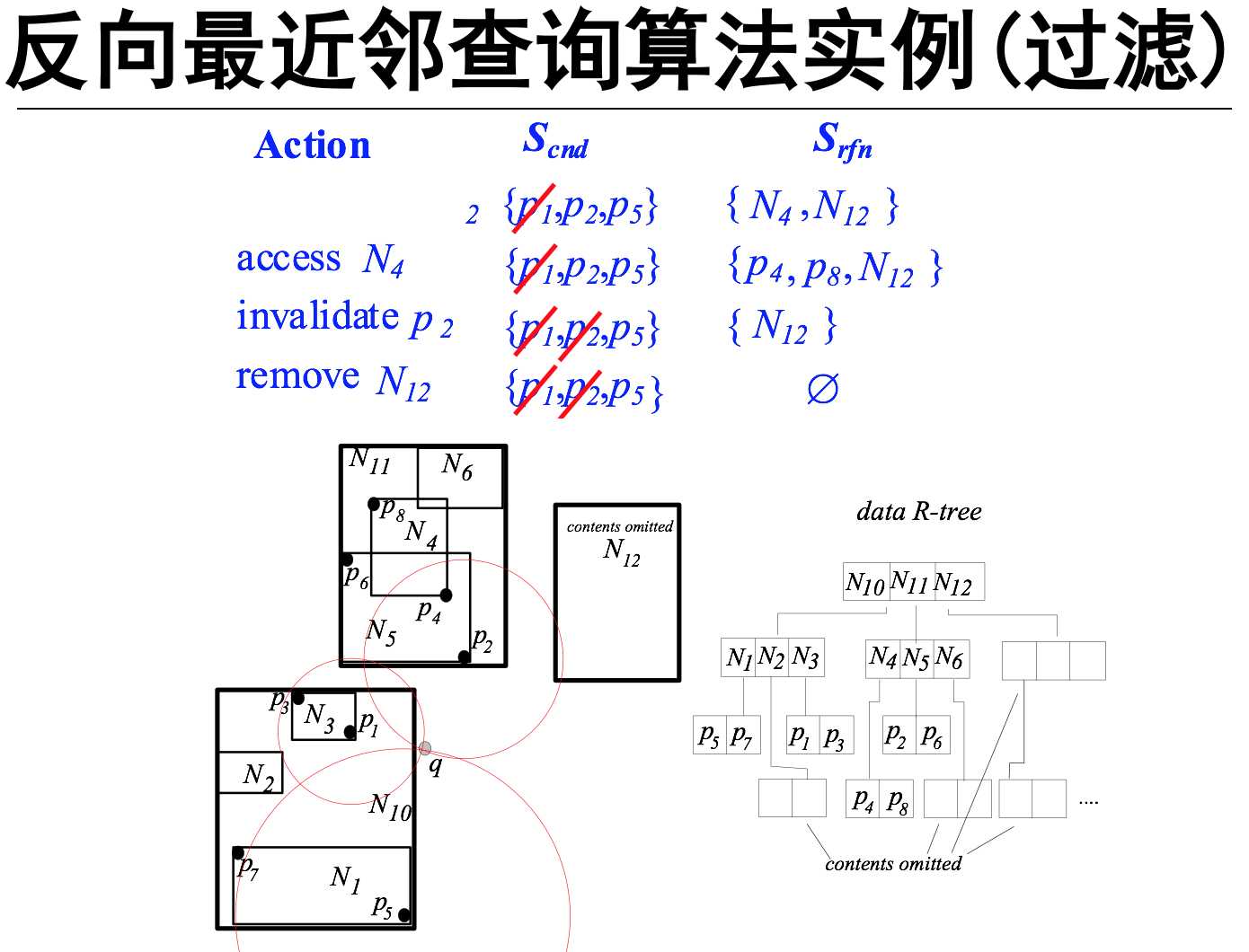
反向最近邻查询(RNN)

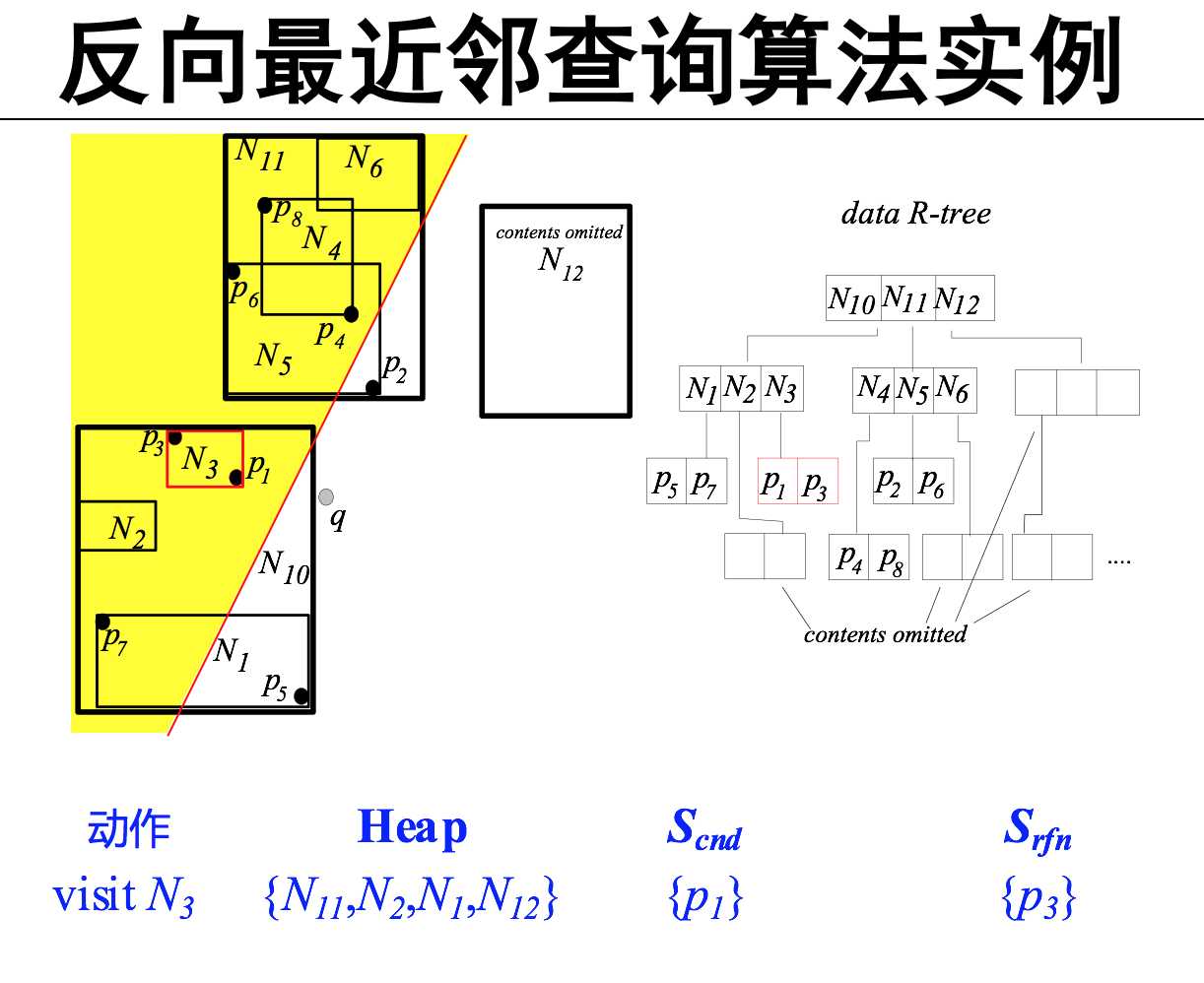
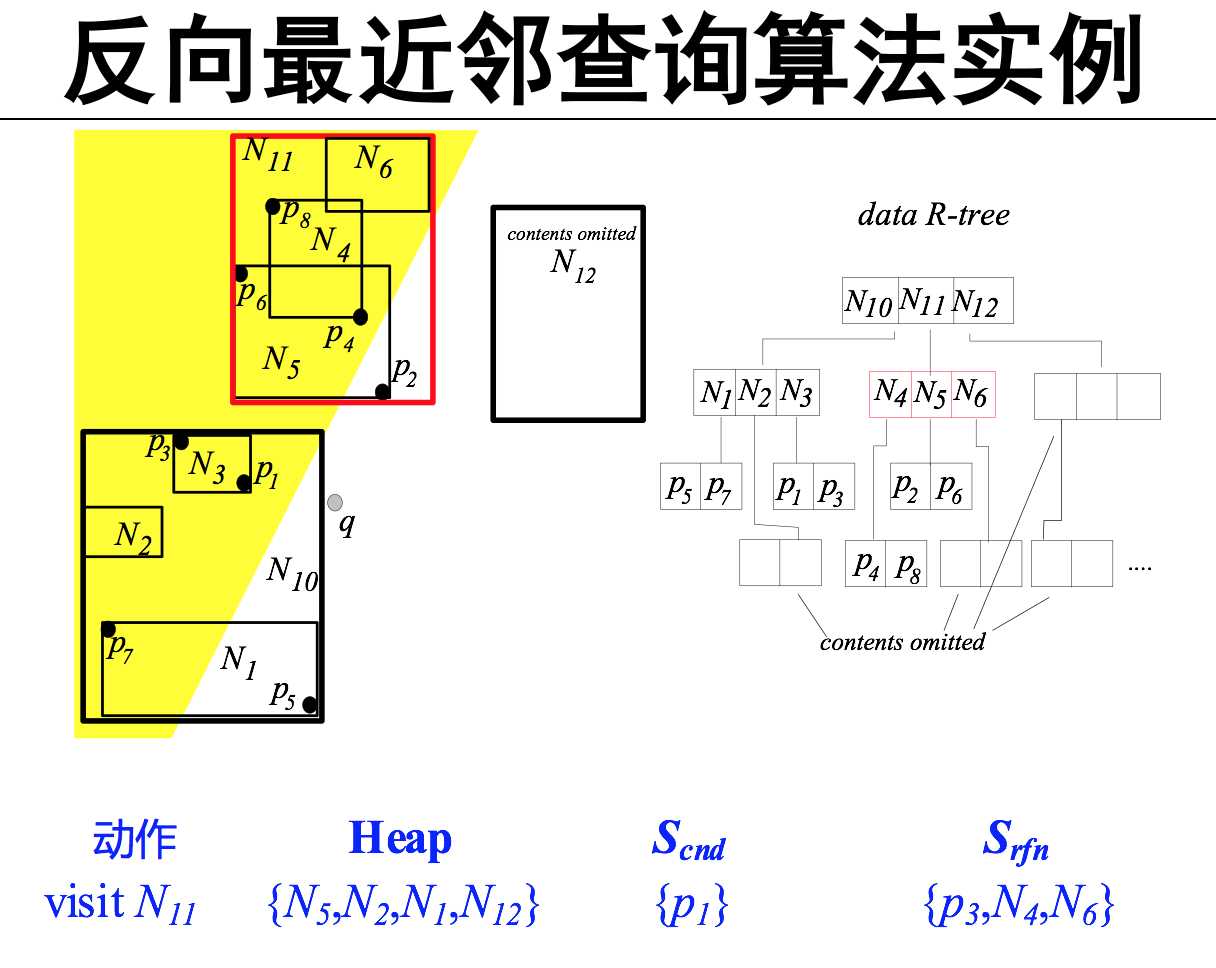
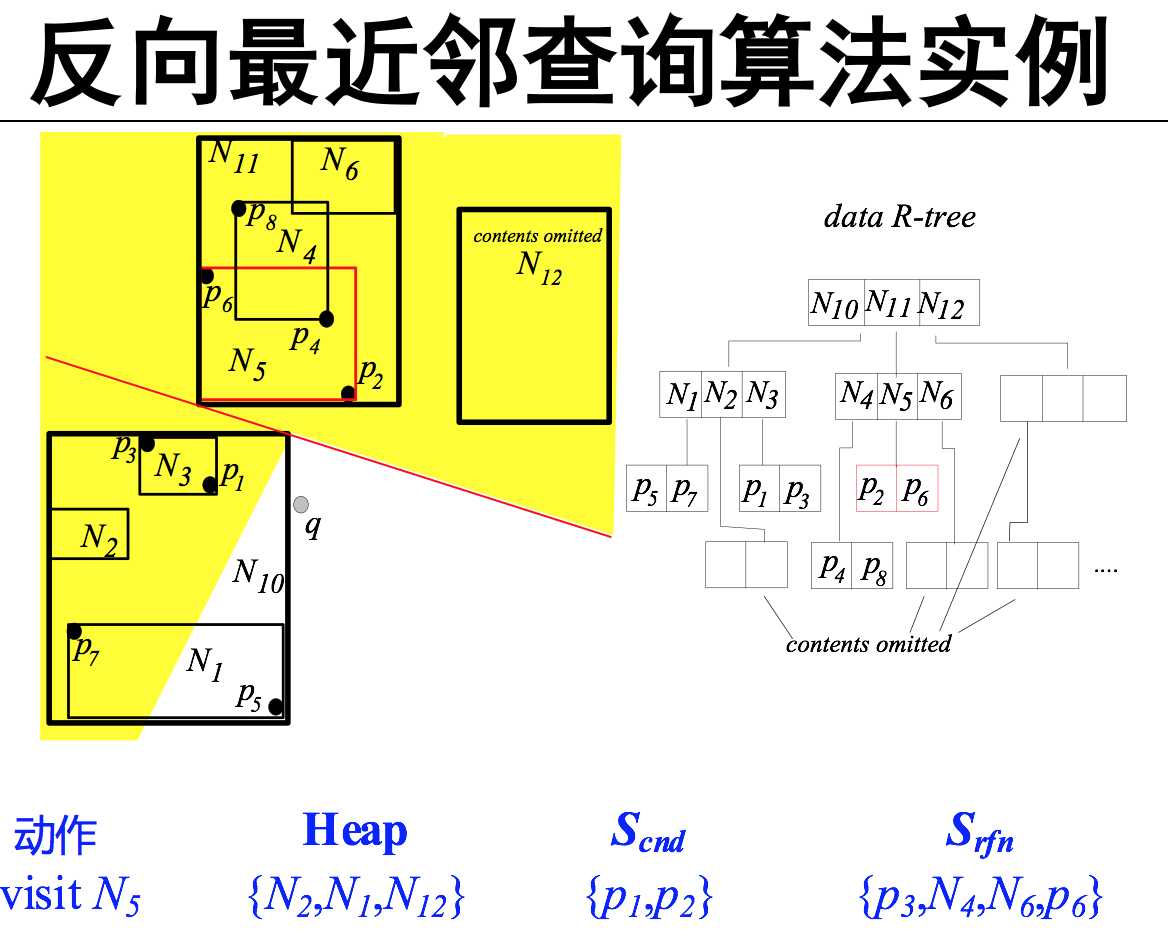
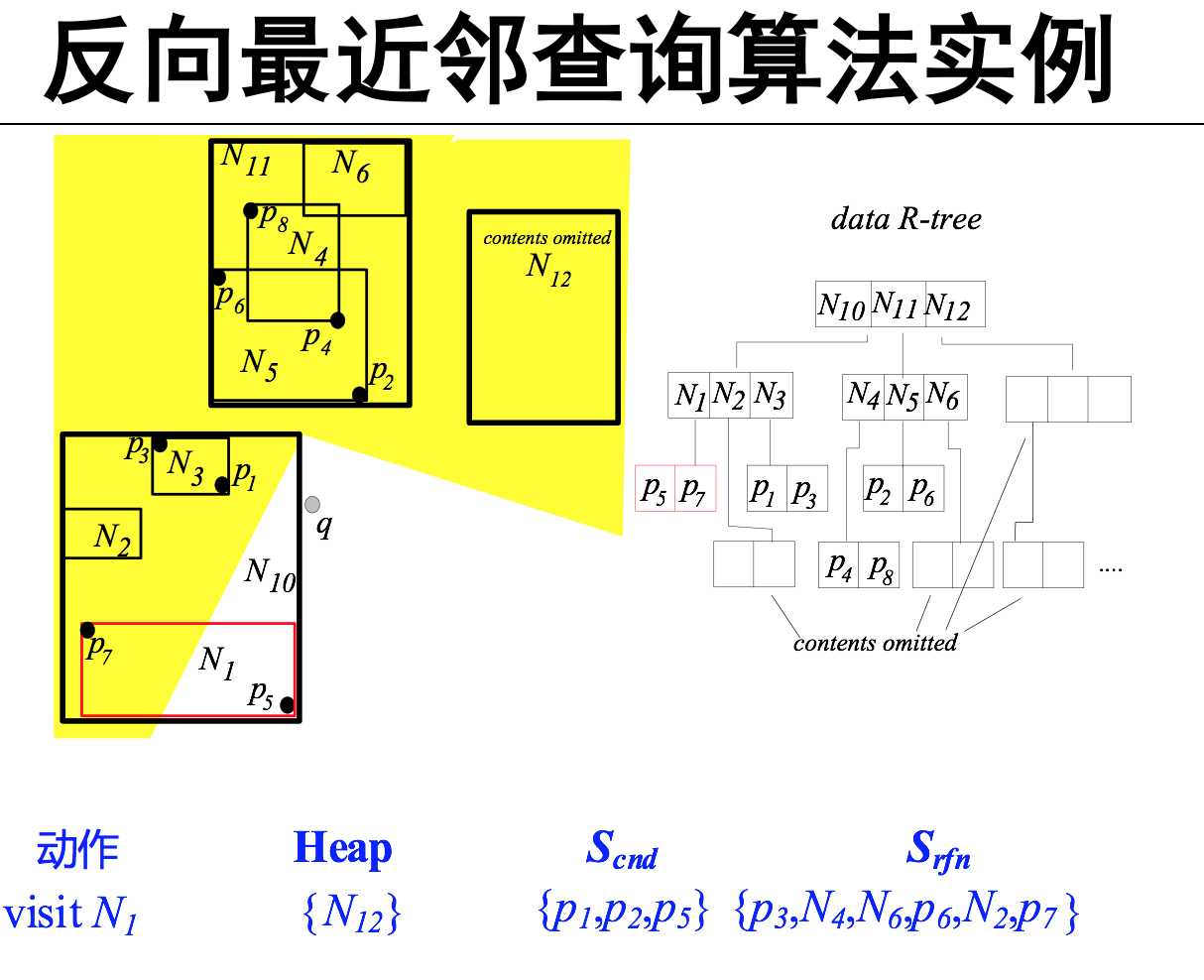
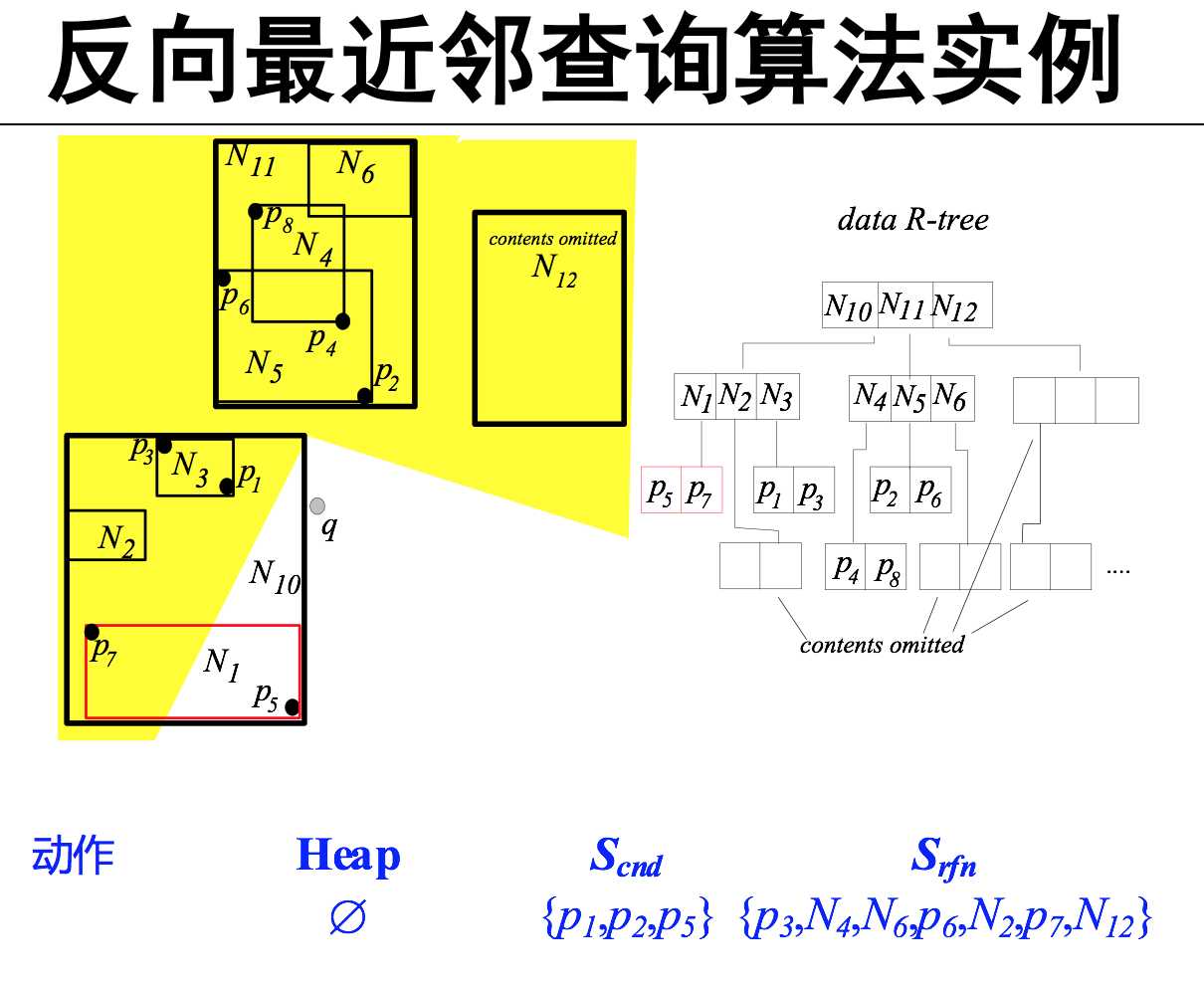
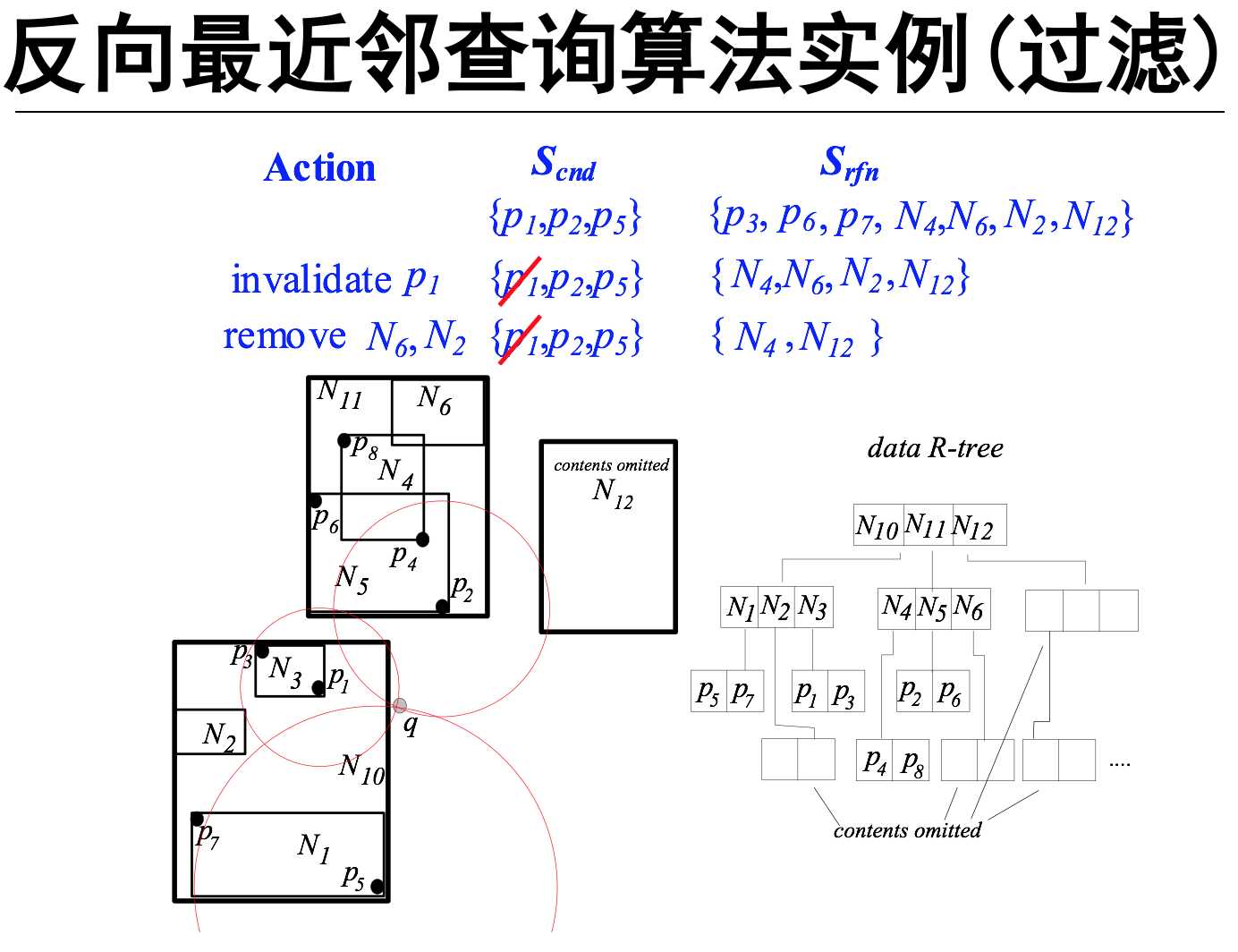
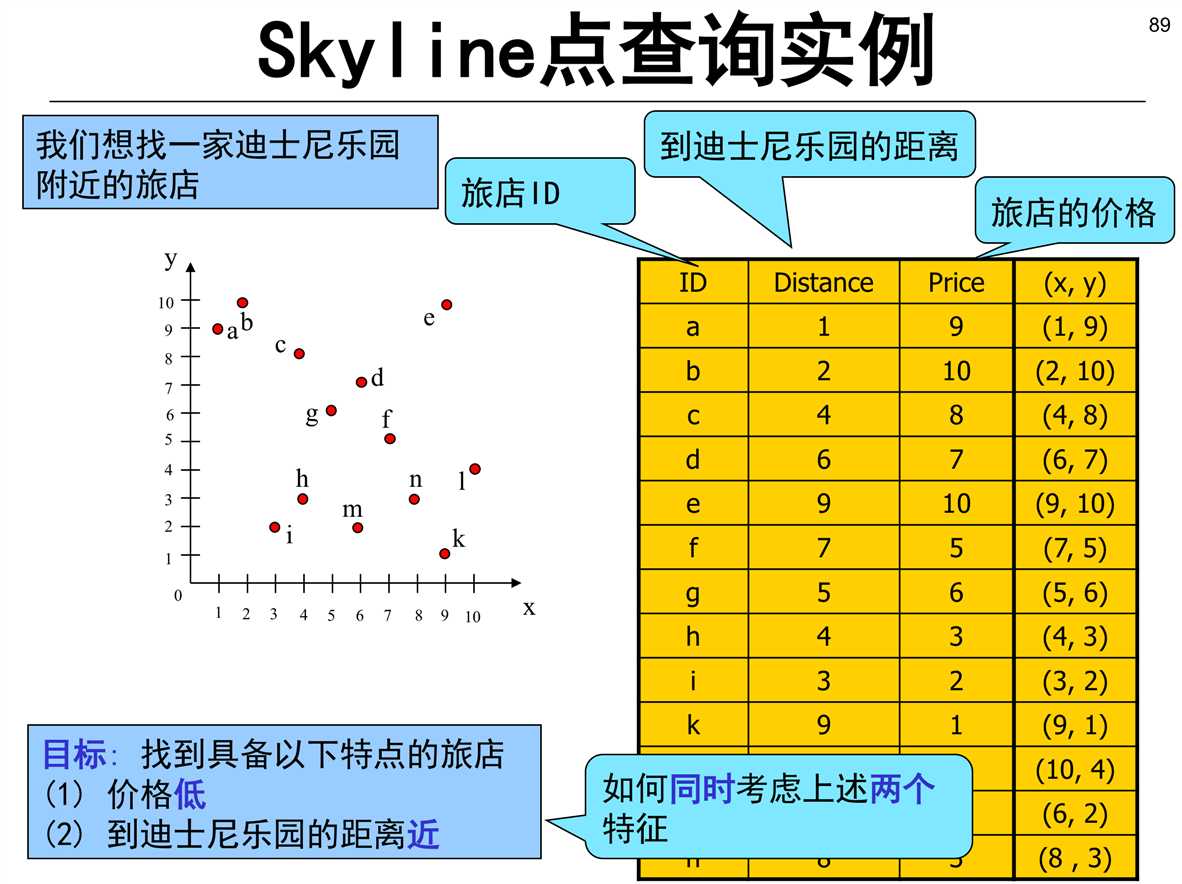
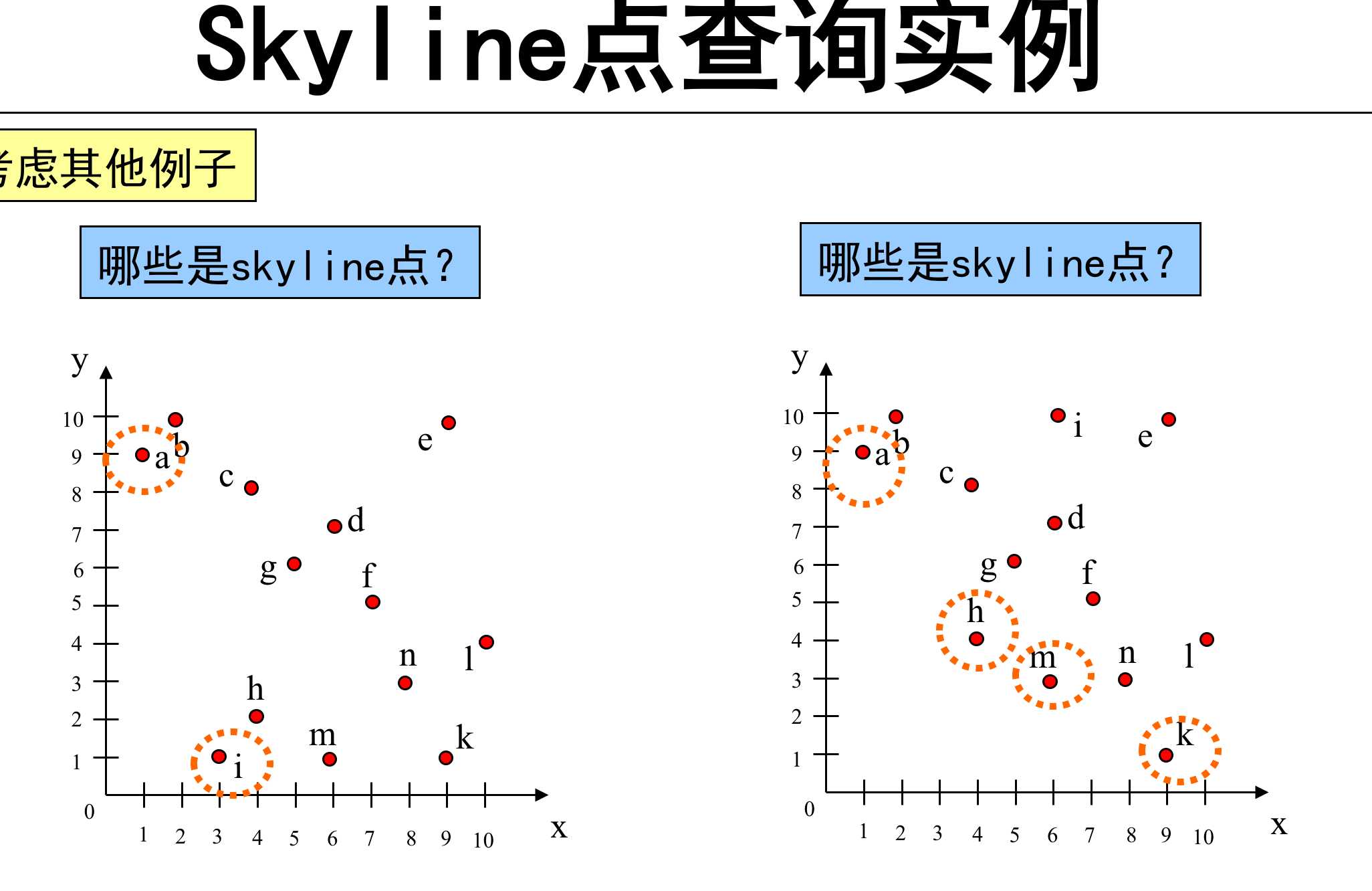
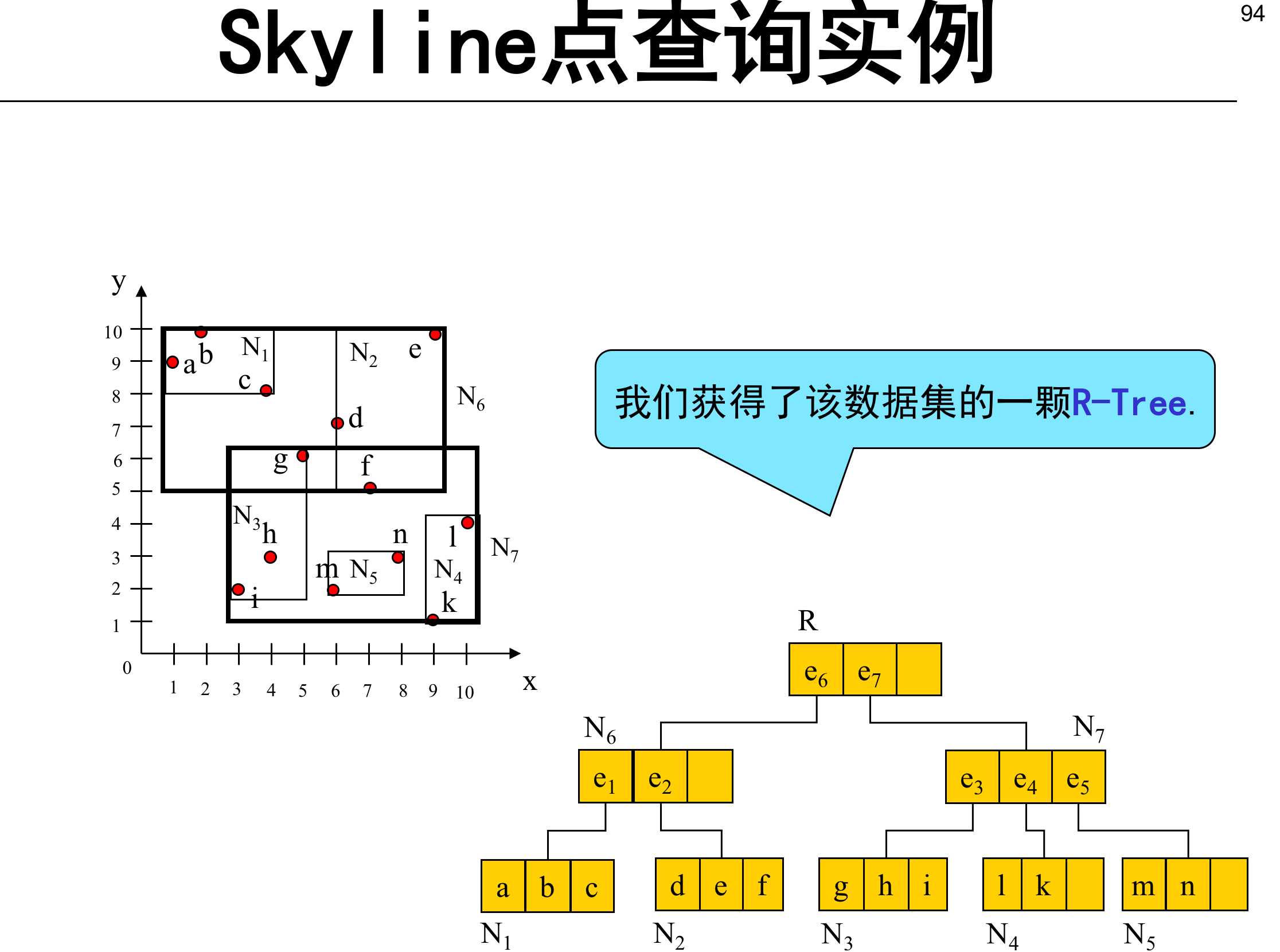
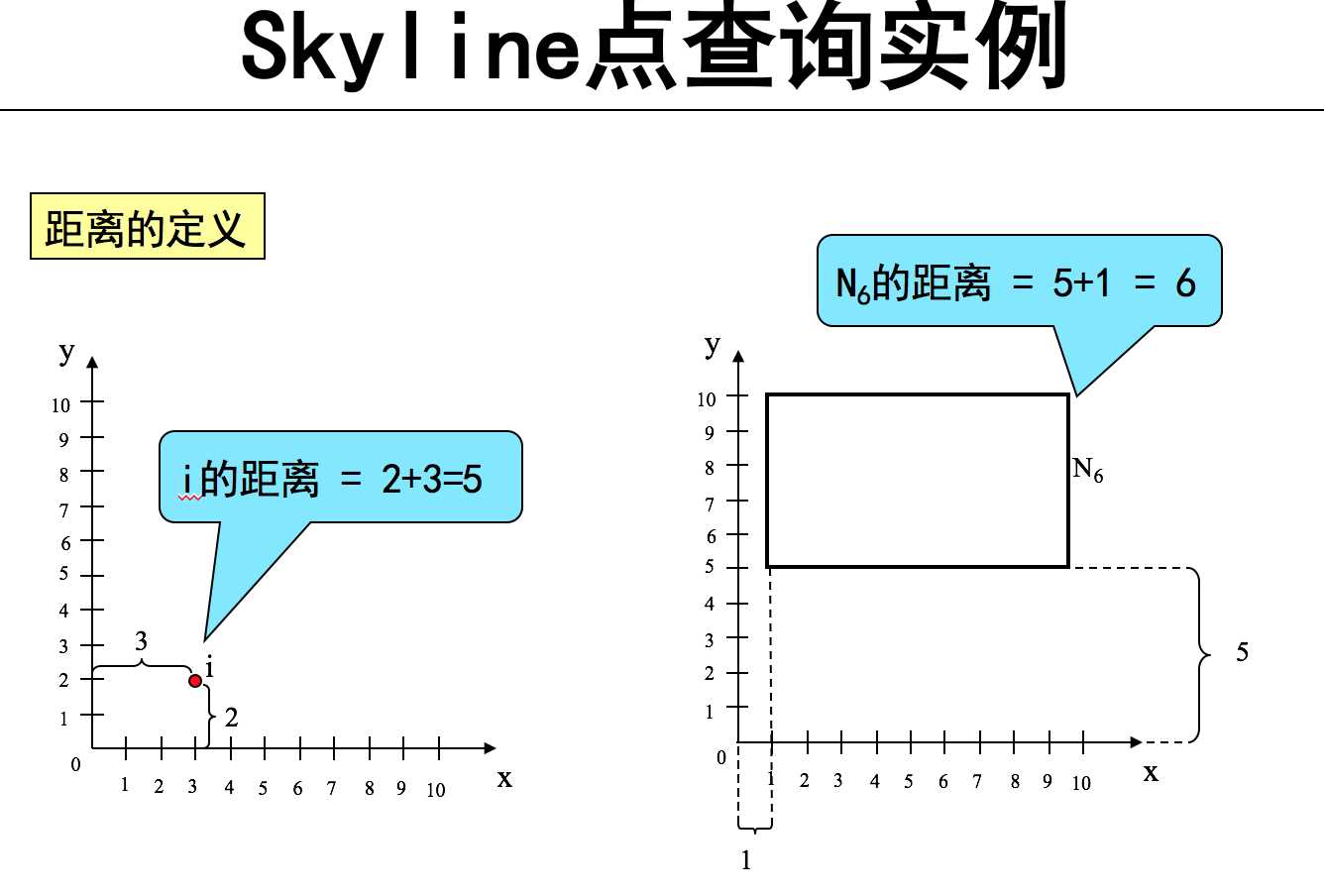
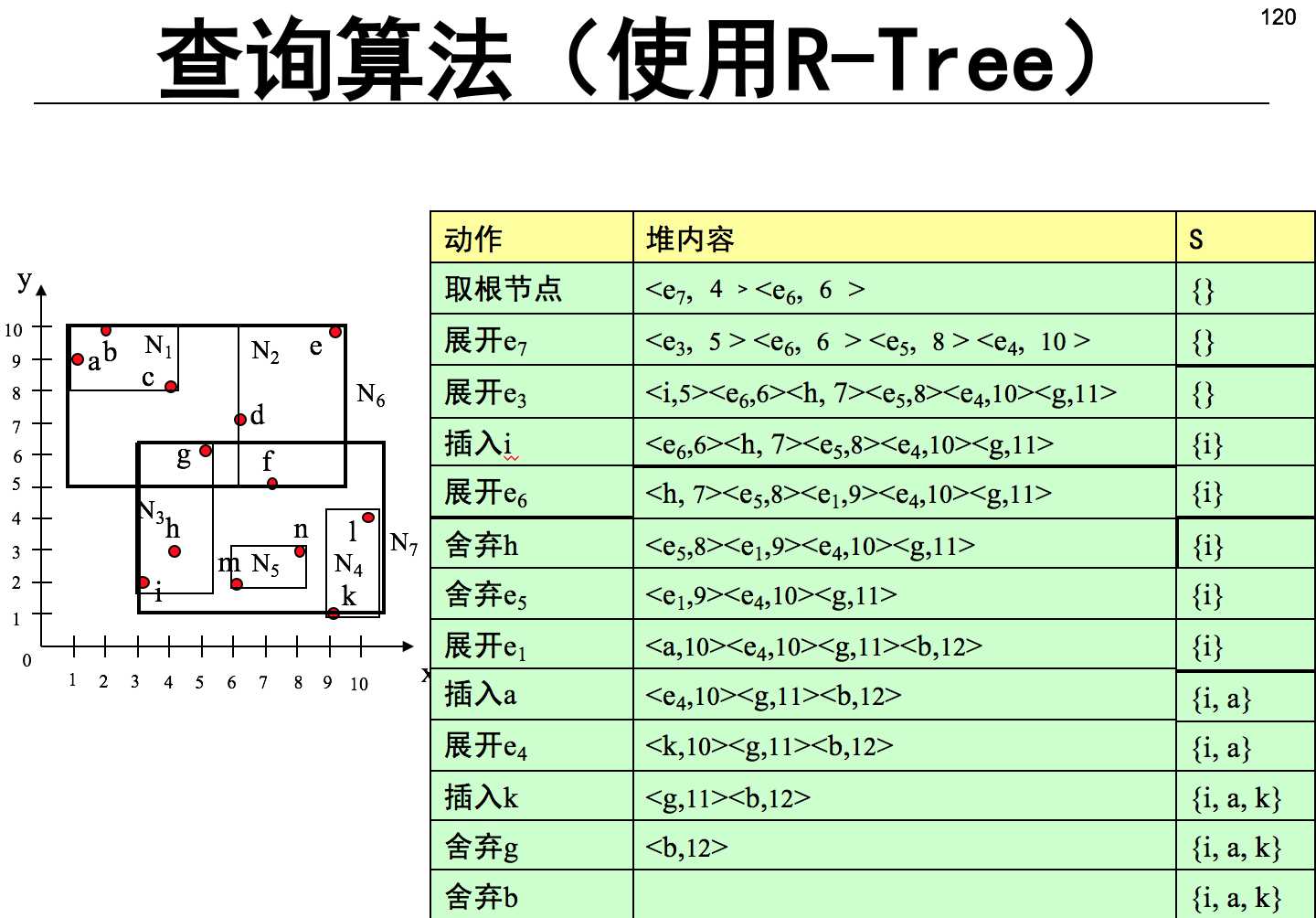
Skyline点 那些点不能被其他的点dominate( 找skyline点集)


参考文献:

Big Spatio temporal Data(R-tree Index and NN & RNN & Skyline)
标签:height 重构 hdfs block 大量 关联分析 其他 资源 选择
原文地址:http://www.cnblogs.com/zpfbuaa/p/6850844.html