标签:min com time operator type tor long ret ++
。。。
果然是dalao们做难题做多了后
简单题水不起来了吗。。
300分
T1写了差不多30~40分钟
T2写了不到5min (当时怀疑有坑..)
T3推了大概1个多小时的式子, 然后又加上调试差不多一个半小时
时间分配就这样..感觉T2出的太过简单了..直接是个模板
T1 并查集 + 乱搞
T2 快速幂模板
T3 Dp
二次联通门 : codevs 2796 最小完全图
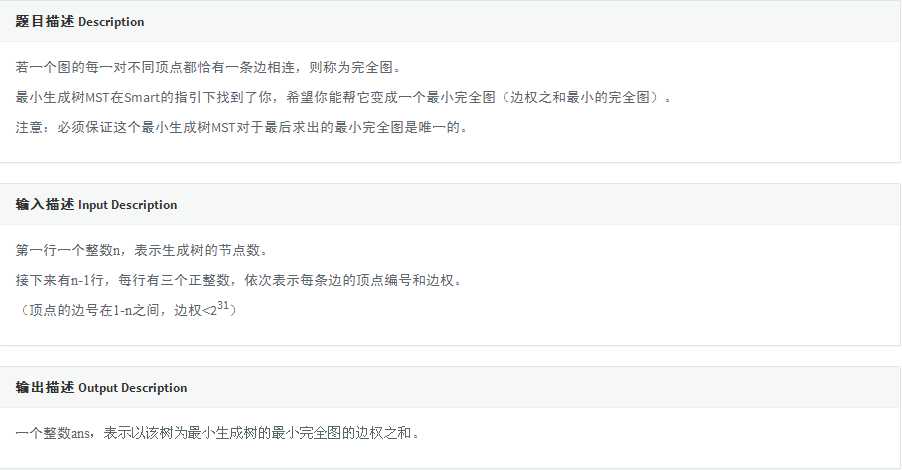
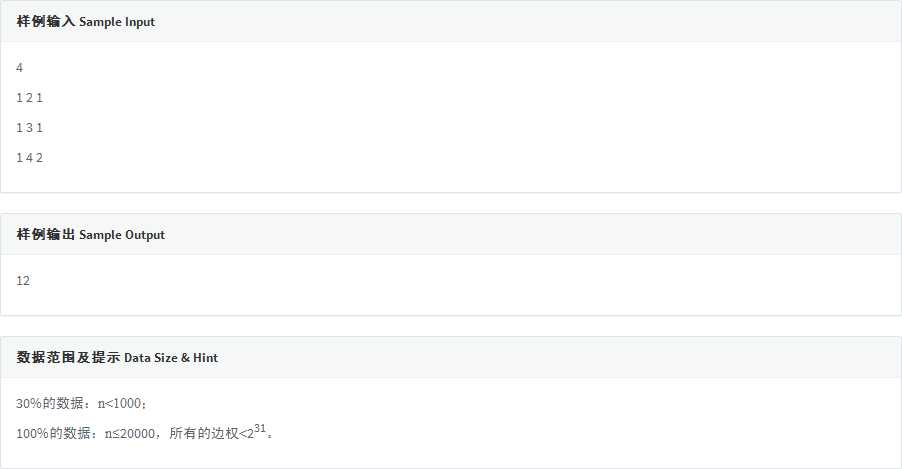
/* codevs 2796 最小完全图 并查集 + 乱搞 用并查集维护图 给并查集带个集合中元素大小的权(即该并查集内共有多少点) 最终的答案就是要合并的两个集合中点数的乘积-1 因为两个集合中的点都不同, 所以可连得边数就是点数的乘积(size[x] * size[y]) 因为这两个集合中已经有当前边了, 所以注意要减去1 由于是求最小 那么边权就是当前边的边权加1啦 (感觉自己说的很迷..) 注意每次合并时记得要按祖先来合并并查集的大小 */ #include <algorithm> #include <cstdio> #define Max 100090 void read (int &now) { now = 0; register char word = getchar (); while (word < ‘0‘ || word > ‘9‘) word = getchar (); while (word >= ‘0‘ && word <= ‘9‘) { now = now * 10 + word - ‘0‘; word = getchar (); } } int N; long long Answer; class Unio_Find_Set_Type { private : int father[Max]; int size[Max]; public : void clear (int N) { for (int i = 1; i <= N; i++) { father[i] = i; size[i] = 1; } } int Find (int x) { return father[x] == x ? x : father[x] = Find (father[x]); } inline void Unio (int x, int y, int dis) { Answer += (long long) (dis + 1) * ((long long) size[x] * (long long) size[y] - 1); size[x] += size[y]; father[y] = x; } }; Unio_Find_Set_Type ZlycerQan; class Make_Graph_Type { private : struct Edges { int from; int to; int dis; bool operator < (const Edges a) const { return dis < a.dis; } } edge[Max]; int Edge_Count; int now_1, now_2; public : inline void Add_Edge (int from, int to, int dis) { Answer += dis; Edge_Count++; edge[Edge_Count].from = from; edge[Edge_Count].to = to; edge[Edge_Count].dis = dis; } void Make () { std :: sort (edge + 1, edge + N); for (int i = 1; i < N; i++) { now_1 = ZlycerQan.Find (edge[i].from); now_2 = ZlycerQan.Find (edge[i].to); ZlycerQan.Unio (now_1, now_2, edge[i].dis); } } }; Make_Graph_Type Make; int main (int argc, char *argv[]) { read (N); int x, y, z; for (int i = 1; i < N; i++) { read (x); read (y); read (z); Make.Add_Edge (x, y, z); } ZlycerQan.clear (N); Make.Make (); printf ("%lld", Answer); return 0; }
T2 : codevs 1497 取余运算
二次联通门 : codevs 1497 取余运算
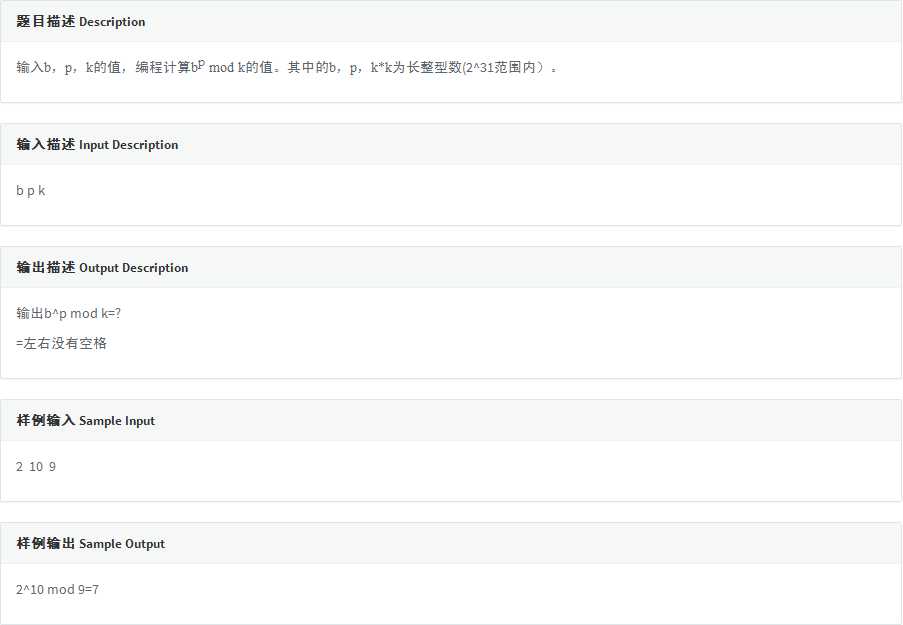
/* codevs 1497 取余运算 快速幂模板.. 不知道为何不能直接用printf 直接把整个式子输出... 就只能比较麻烦, 分开输出了.. */ #include <cstdio> void read (long long &now) { now = 0; register char word = getchar (); while (word < ‘0‘ || word > ‘9‘) word = getchar (); while (word >= ‘0‘ && word <= ‘9‘) { now = now * 10 + word - ‘0‘; word = getchar (); } } long long Fast_Pow (long long now, long long p, long long Mod) { long long Answer = 1; while (p) { if (p & 1) Answer = (Answer * now) % Mod; now = (now * now) % Mod; p >>= 1; } return Answer; } int main (int argc, char *argv[]) { long long x, p, Mod; read (x); read (p); read (Mod); printf ("%lld^", x); printf ("%lld mod", p); printf (" %lld=", Mod); printf ("%lld", Fast_Pow (x, p, Mod)); return 0; }
T3 : codevs 1257 打砖块
二次联通门 : codevs 1257 打砖块
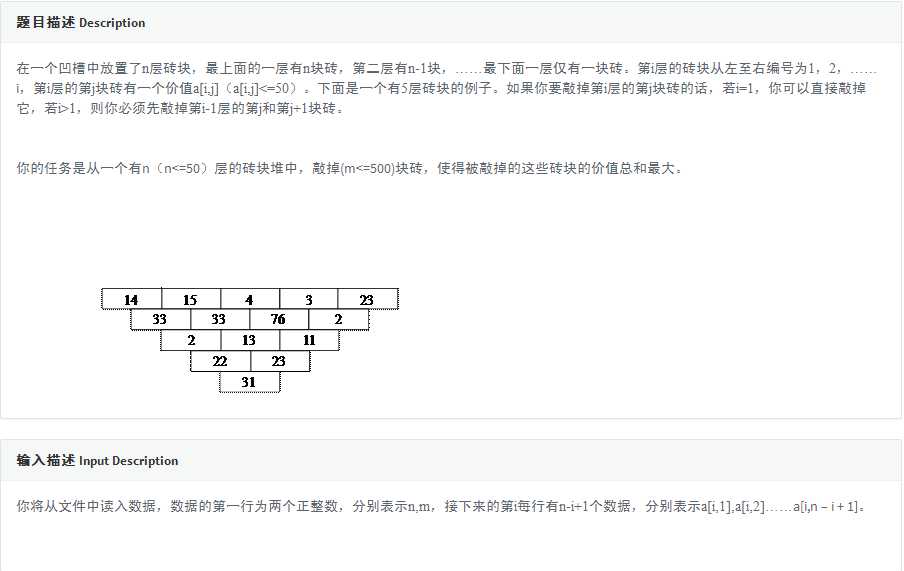
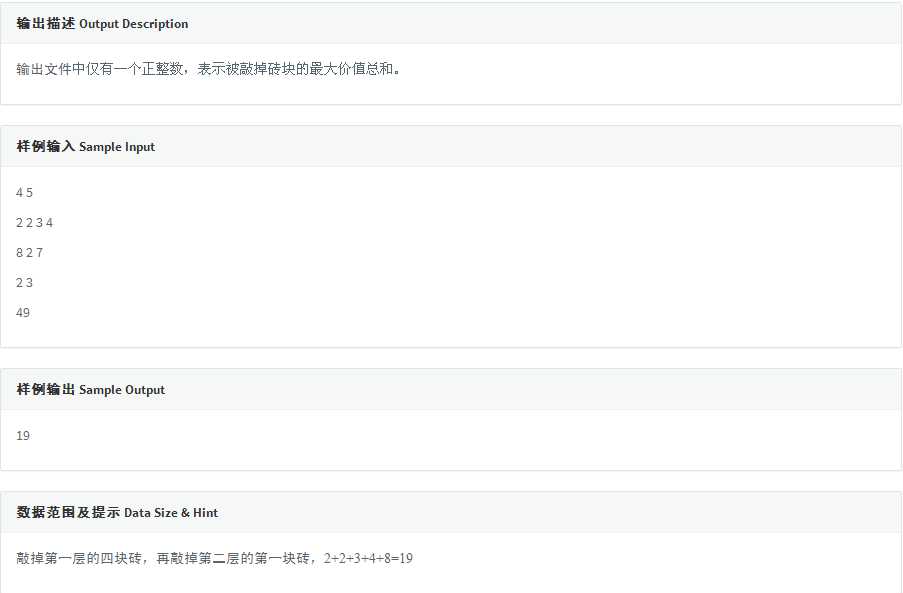
/* codevs 1257 打砖块 DP 状态数很好确定 dp[i][j][k] 表示 打到第i行第j列是第k个被打掉的最大价值 那么方程就是 dp[i][j][k] = max (dp[i][j][k], dp[i + 1][p][k - j] + map[j][i]) map[i][j]是个前缀和 用来记录(1 ~ i)行中第j列的价值总和 p是枚举当前列中的位置 若砖块不是按照顺序打掉的(即类似于一个三角形), 则新开一列 第0列 即dp[i][0][k], 存的是不打第i列的砖块 打第i-1列中砖块的最大值 这样递推一下就可以.. 注意边界条件, 和每一行中的k值的正确求出 */ #include <cstdlib> #include <cstdio> #include <ctime> #define Max 105 #define V N - i + 1 void read (int &now) { now = 0; register char word = getchar (); while (word < ‘0‘ || word > ‘9‘) word = getchar (); while (word >= ‘0‘ && word <= ‘9‘) { now = now * 10 + word - ‘0‘; word = getchar (); } } inline int max (int a, int b) { return a > b ? a : b; } int N, M; int dp[Max][Max][Max * 10]; int map[Max][Max]; int main (int argc, char *argv[]) { read (N); read (M); for (int i = 1; i <= N; i++) for (int j = 1; j <= V; j++) { read (map[i][j]); map[i][j] += map[i - 1][j]; } int Answer = 0, now; for (int i = N; i >= 1; i--) for (int j = 0; j <= V; j++) { now = 0; for (int q = 1; q <= j; q++) now += q; if (j == 0) now = 1; for (int k = now; k <= M; k++) for (int p = j - 1; p <= V; p++) if (p >= 0) dp[i][j][k] = max (dp[i][j][k], dp[i + 1][p][k - j] + map[j][i]); else dp[i][j][k] = max (dp[i][j][k], dp[i + 1][0][k - j] + map[j][i]); } for (int i = 1; i <= N; i++) for (int j = 0; j <= V; j++) Answer = max (Answer, dp[i][j][M]); printf ("%d", Answer); return 0; }
标签:min com time operator type tor long ret ++
原文地址:http://www.cnblogs.com/ZlycerQan/p/6853559.html