标签:利用 表格 步骤 目的 随机 化学 样本 医院 code
在机器学习中,特征选择主要有两个目的:
1. 减少特征数量,提高训练速度
2. 减少噪声特征从而提高模型在测试集上的准确率。一些噪声特征会导致模型出现错误的泛化,容易产生overfitting。
常用的特征选择算法有很多,这里着重介绍其中两个:卡方检验和互信息
一、卡方检验
1. 卡方分布
在说卡方检验之前,首先介绍卡方分布。
设 X1, X2, ..., Xn 是来自总体 N(0,1) 的独立样本,那么统计量 $X^{2}=X_{1}^{2}+X_{2}^{2}+...+X_{n}^{2}$ 服从自由度为 n 的卡方分布,记为 $X^{2} \sim X^{2}(n)$. 注意,这里的自由度是指公式右端独立变量的个数,与卡方检验中的自由度不同。
卡方分布的性质:
a. 期望 $E(X^{2})=n$
b. 方差 $D(X^{2})=2n$
c. 分位点 $P{X^{2}>X_{\alpha}^{2}(n)}=\alpha$, 如下图所示
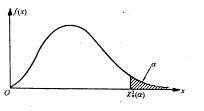
2. 卡方检验
即 Χ2 检验,它是数理统计中常用的检验两个变量独立性的方法。首先假设两个变量时独立的(原假设),然后计算观察值与理论值的偏差。如果偏差足够小,那么就接受原假设,否则,拒绝原假设,接受备择假设。偏差的计算公式如下
$\sum_{i=1}^{n}\frac{(x_{i}-E)^{2}}{E}$ (1)
其中,$x_{i}$是样本的观察值,$E$ 是理论值。计算出来的偏差值与卡方表中的阈值(根据显著性水平$\alpha$确定)对比,如果小于此阈值,则原假设成立,否则,拒绝原假设。
2.1 四格表
顾名思义,四格表,即具有四个格子的表,举个栗子来说明:
某医院分别利用化学疗法和化疗结合放射治疗卵巢癌患者,结果如表,请问两种疗法有无差别?
| 组别 | 有效 | 无效 | 合计 | 有效率(%) |
| 化疗组 | 19 | 24 | 43 | 44.2 |
| 化疗加放射 | 34 | 10 | 44 | 77.3 |
| 合计 | 53 | 34 | 87 | 60.9 |
表格中最原始的数据有四个(19, 24, 34, 10),其他数据都是由这四个数据推导而来。那么如何利用公式来计算卡方值呢?这里涉及到理论值计算 。假设治疗方法的不同对治疗结果没有影响,即化疗与化疗加放射这两个随机变量之间没有关系。注:卡方检验的自由度,在这里计算方法是:v = (行数-1)(列数-1)
2.2 检验步骤:
a. 建立检验假设
$H_{0}$: 治疗方法对治疗结果没有影响
$H_{1}$: 治疗方法对治疗结果有影响
$\alpha$=0.01
b. 计算理论值
| 组别 | 有效 | 无效 | 合计 |
| 化疗 | 26.2 | 16.8 | 43 |
| 化疗加放射 | 26.8 | 17.2 | 44 |
| 合计 | 53 | 34 | 87 |
因为已经假设了治疗方法对治疗结果没有影响。这里仍利用第一个表中总的有效率(即60.9%),化疗组共有43个样本,有效的应该是 43*60.9% = 26.2 。 其他3个同样的计算方法得到。这样,有了观察值和理论值,就可以计算卡方值了。
c. 计算卡方值
把观察值表和理论值表代入到公式(1)中,
$X^{2}=\sum_{i=1}^{n}\frac{(x_{i}-E)^{2}}{E}=\frac{(19-26.2)^{2}}{26.2}+\frac{(24-16.8)^{2}}{16.8}+\frac{(34-26.8)^{2}}{26.8}+\frac{(10-17.2)^{2}}{17.2}=10.01$
d. 查表对比卡方值与阈值
根据查表得知(表可以在书上或者网上查到),$X^{2}_{0.01}(1)=6.63$, (注:$X^{2}_{\alpha}(v)$), 卡方值(10.01) > 阈值(6.63),所以我们拒绝原假设,接受备择假设,即治疗方法对治疗结果有影响。
3. Python 实现
在Python中实现卡方检验有两种方法,一种是利用scipy,另一种是利用 sklearn。
3.1 scipy
import scipy from scipy.stats import chisquare chisquare([5, 2, 0, 13, 14]) # Power_divergenceResult(statistic=23.941176470588239, pvalue=8.2072801249491787e-05)
具体关于 chisquare 的用法请参考scipy的doc.
3.2 sklearn
TBD
二、互信息(Mutual Information)
1. 定义
互信息是用来评价一个事件的出现对于另一个事件的出现所贡献的信息量,互信息的定义如下
$I(Y;X)=\sum_{y_{i} \in Y} \sum_{x_{i} \in X} P(X=x_{i}, Y=y_{i})log_{2}\frac{P(X=x_{i}, Y=y_{i})}{P(X=x_{i}) P(Y=y_{i})}$
在对文本进行特征选择的时候,X表示某个词,Y表示类别,$x_{i}$表示这个词的取值(0, 1),分别是出现和不出现;$y_{i}$表示类别,可以为两类或者多类。
对文本特征提取$x_{i}$的取值只能是出现和不出现两种情况。使用互信息理论进行特征抽取是基于如下假设:在某个特定类别出现频率高,但在其他类别出现频率较低的词条与该类的互信息较大。通常互信息作为特征词与类别之间的测度,如果特征词属于该类,它们的互信息最大。特征项和类别的互信息体现了特征项与类别的相关程度,是一种广泛用于建立词关联统计模型的标准。
2. Python实现
好像有一个包可以用,minepy,具体的没有研究,可以搜下,github上有这个项目。
标签:利用 表格 步骤 目的 随机 化学 样本 医院 code
原文地址:http://www.cnblogs.com/satchel/p/6856663.html