题目描述
如题,给出一个无向图,求出最小生成树,如果该图不连通,则输出orz
输入输出格式
输入格式:
第一行包含两个整数N、M,表示该图共有N个结点和M条无向边。(N<=5000,M<=200000)
接下来M行每行包含三个整数Xi、Yi、Zi,表示有一条长度为Zi的无向边连接结点Xi、Yi
输出格式:
输出包含一个数,即最小生成树的各边的长度之和;如果该图不连通则输出orz
输入输出样例
输入样例#1:
4 5 1 2 2 1 3 2 1 4 3 2 3 4 3 4 3
输出样例#1:
7
说明
时空限制:1000ms,128M
数据规模:
对于20%的数据:N<=5,M<=20
对于40%的数据:N<=50,M<=2500
对于70%的数据:N<=500,M<=10000
对于100%的数据:N<=5000,M<=200000
样例解释:
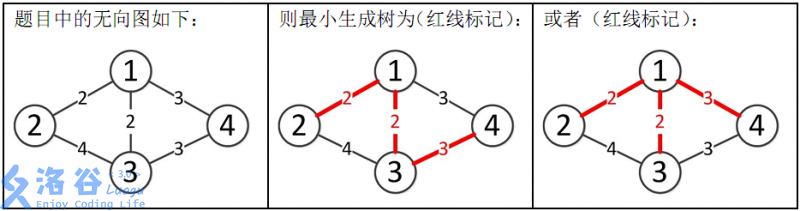
所以最小生成树的总边权为2+2+3=7
p算法代码:(错了,哪位大佬帮我看看!)
#include<stdio.h> #include<cstdlib> #include<cstring> #include<iostream> #include<algorithm> #define N 5001 #define maxn 1234567 using namespace std; int read() { int x=0,f=1; char ch=getchar(); while(ch<‘0‘||ch>‘9‘) { if(ch==‘-‘) f=-1; ch=getchar(); } while(ch<=‘9‘&&ch>=‘0‘) { x=x*10+ch-‘0‘; ch=getchar(); } return f*x; } int n,m,x,y,z,a[N][N],dis[N],ans; bool b[N]; int main() { memset(b,false,sizeof(b)); n=read(),m=read(); for(int i=1;i<=m;i++) { x=read(),y=read(),z=read(); a[x][y]=a[y][x]=z; } memset(dis,127,sizeof(dis)); b[1]=true; dis[1]=0; for(int i=1;i<=n;i++) if(a[1][i]) dis[i]=min(dis[i],a[1][i]); for(int i=1;i<n;i++) { int maxd=0; for(int j=1;j<=n;j++) { if(!b[j]) if(maxd==0||dis[j]<dis[maxd]) maxd=j; } ans+=dis[maxd]; b[maxd]=true; for(int j=1;j<=n;j++) { if(!b[j]) if(a[maxd][j]) dis[j]=min(dis[j],a[maxd][j]); } } if(ans>=maxn) { printf("orz"); return 0; } printf("%d\n",ans); return 0; }
k算法代码
#include<stdio.h> #include<cstdlib> #include<cstring> #include<iostream> #include<algorithm> #define N 200001 #define maxn 1234567 using namespace std; int n,m,x,y,z,ans,tot,fa[N]; struct Edge { int x,y,z; }edge[N]; int read() { int x=0,f=1; char ch=getchar(); while(ch<‘0‘||ch>‘9‘) { if(ch==‘-‘) f=-1; ch=getchar(); } while(ch<=‘9‘&&ch>=‘0‘) { x=x*10+ch-‘0‘; ch=getchar(); } return f*x; } int found(int x) { return fa[x]==x?x:fa[x]=found(fa[x]); } int cmp(Edge a,Edge b) { return a.z<b.z; } int main() { n=read(),m=read(); for(int i=1;i<=m;i++) { x=read(),y=read(),z=read(); edge[i].x=x; edge[i].y=y; edge[i].z=z; } sort(edge+1,edge+1+m,cmp); for(int i=1;i<=n;i++) fa[i]=i; for(int i=1;i<=m;i++) { x=edge[i].x,y=edge[i].y; int fx=found(x),fy=found(y); if(fx==fy) continue; fa[fx]=fy; tot++; ans+=edge[i].z; if(tot==n-1) break; } int fx=found(1); for(int i=2;i<=n;i++) { if(found(i)!=fx) { printf("orz"); return 0; } } printf("%d",ans); return 0; }
