标签:元素 style 基本使用 转化 targe 再计算 目标 组成 数学
机器学习是实现人工智能的手段, 其主要研究内容是如何利用数据或经验进行学习, 改善具体算法的性能
多领域交叉, 涉及概率论、统计学, 算法复杂度理论等多门学科
广泛应用于网络搜索、垃圾邮件过滤、推荐系统、广告投放、信用评价、欺诈检测、股票交易和医疗诊断等应用
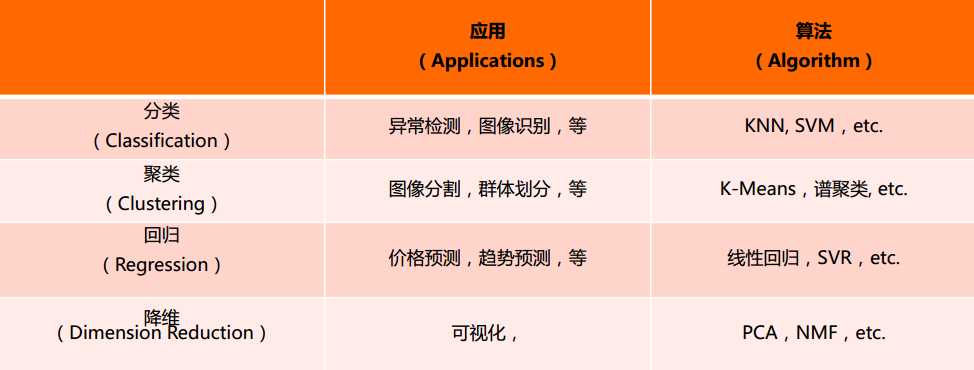
机器学习的分类
监督学习 (Supervised Learning)
从给定的数据集中学习出一个函数, 当新的数据到来时, 可以根据这个函数预测结果, 训练集通常由人工标注
无监督学习 (Unsupervised Learning)
相较于监督学习, 没有人工标注
强化学习(Reinforcement Learning,增强学习)
通过观察通过什么样的动作获得最好的回报, 每个动作都会对环境有所影响, 学习对象通过观察周围的环境进行判断
半监督学习(Semi-supervised Learning)
介于监督学习和无监督学习
深度学习 (Deep Learning)
利用深层网络神经模型, 抽象数据表示特征
在Python中使用Scikit-learn(简化为sklearn)这一模块来处理机器学习
主要是依赖于numpy, scipy和matplotlib库
开源可复用
sklearn中机器学习模型十分丰富, 需要根据问题的类型来选择适当的模型
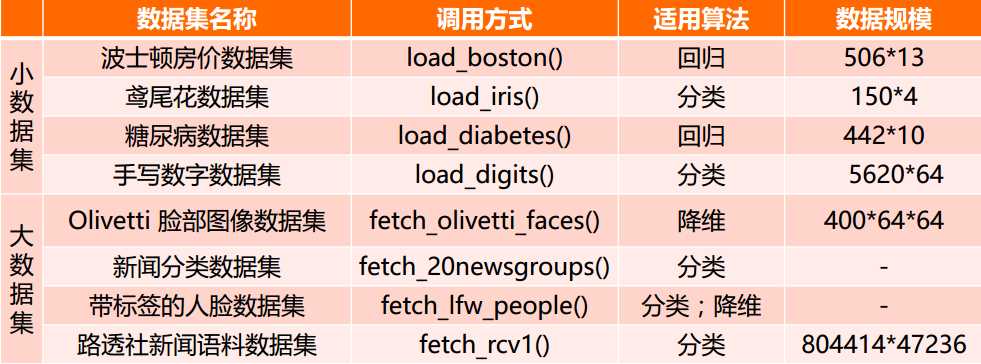
sklearn常用的函数
关于sklearn库
sklearn是scikit-learn的简称,是一个基于Python的第三方模块。sklearn库集成了一些常用的机器学习方法,在进行机器学习任务时,并不需要实现算法,只需要简单的调用sklearn库中提供的模块就能完成大多数的机器学习任务。
安装sklearn库需要安装numpy, scipy(sklearn的基础, 集成了多种数学算法和函数), matplotlib(数据绘图工具)
注意安装有顺序: numpy -> scipy -> matplotlib -> sklearn
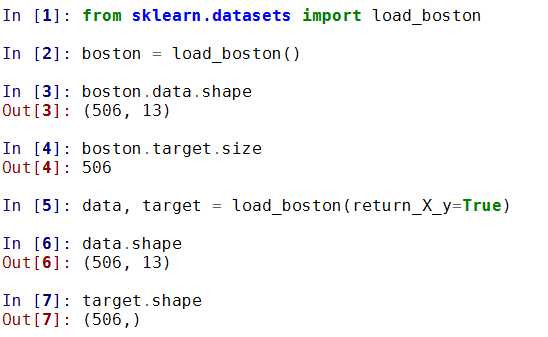
1) 波士顿房价数据集
波士顿房价数据集包含506组数据,每条数据包含房屋以及房屋周围的详细信息。其中包括城镇犯罪率、一氧化氮浓度、住宅平均房间数、到中心区域的加距离以及自住房平均房价等。因此,波士顿房价数据集能够应用到回归问题上。
加载数据集
sklearn.datasets.load_boston()
其中有参数return_X_y, 设置为True是会返回(data, target)两个数据, 默认为False, 只返回data(包含了data和target两个部分的内容)
具体使用
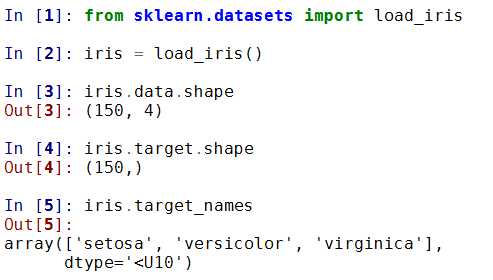
2) 鸢尾花数据集
鸢尾花数据集采集的是鸢尾花的测量数据以及其所属的类别
测量数据包括: 萼片长度、萼片宽度、花瓣长度、花瓣宽度
类别共分为三类: Iris Setosa,Iris Versicolour,Iris Virginica, 该数据集可用于多分类问题
加载数据集
sklearn.datasets. load_iris()
同样有参数return_X_y, 使用方法雷同
具体实例
3) 手写数字数据集
手写数字数据集包括1797个0-9的手写数字数据,每个数字由8*8大小的矩阵构成,矩阵中值的范围是0-16,代表颜色的深度。
加载数据集
sklearn.datasets.load_digits()
return_X_y: 效果依旧, True返回(data, target), 默认False直接返回全部内容
n_class: 设置数据类别, 返回数据的类别比设置类别低的数据样本, 设置为5就会返回0~4的数据
基本使用

sklearn库的共分为6大部分,分别用于完成分类任务、回归任务、聚类任务、降维任务、 模型选择以及数据的预处理
1) 分类任务

2) 回归任务
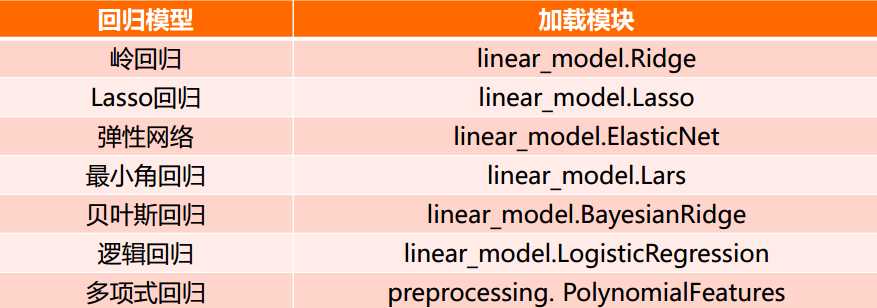
3) 聚类任务
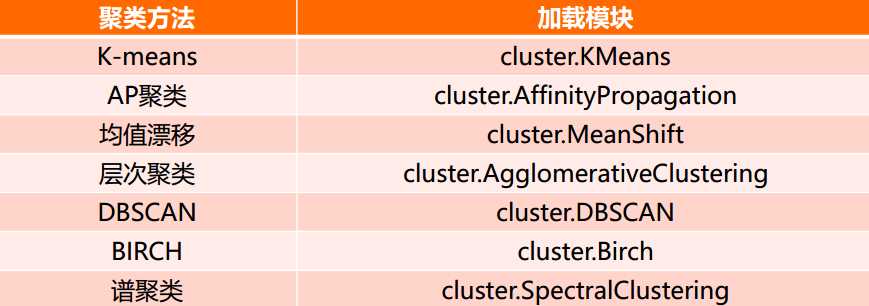
4) 降维任务
无监督学习的目标
利用无标签的数据学习数据的分布或数据与数据之间的关系被称作无监督学习
有监督学习和无监督学习的最大区别在于数据是否有标签
无监督学习最常应用的场景是聚类(clustering)和降维(DimensionReduction)
聚类
聚类(clustering),就是根据数据的“相似性”将数据分为多类的过程
评估两个不同样本之间的“相似性” ,通常使用的方法就是计算两个样本之间的“距离”。使用不同的方法计算样本间的距离会关系到聚类结果的好坏
1) 欧氏距离
欧氏距离是最常用的一种距离度量方法,源于欧式空间中两点的距离。
计算公式
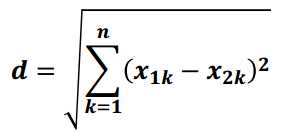
直观表示
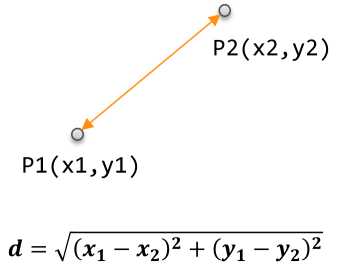
2) 曼哈顿距离
曼哈顿距离也称作“城市街区距离”,类似于在城市之中驾车行驶,从一个十字路口到另外一个十字楼口的距离
计算公式
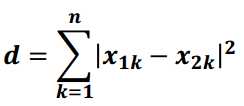
直观表示
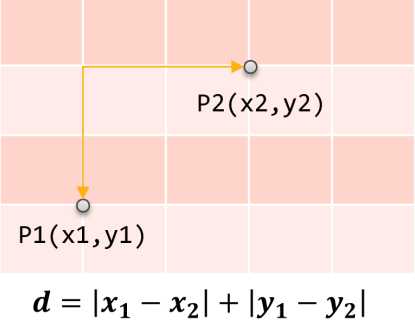
3) 马氏距离
马氏距离表示数据的协方差距离,是一种尺度无关的度量方式。也就是说马氏距离会先将样本点的各个属性标准化,再计算样本间的距离。
计算公式, 其中s是协方差矩阵
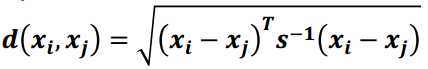
马氏空间的距离

4) 夹角余弦
余弦相似度用向量空间中两个向量夹角的余弦值作为衡量两个样本差异的大小。余弦值越接近1,说明两个向量夹角越接近0度,表明两个向量越相似
计算公式
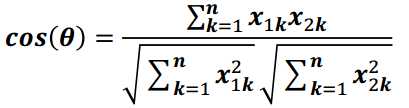
二维空间显示
sklearn提供的常用聚类算法函数包含在sklearn.cluster这个模块中
以同样的数据集应用于不同的算法,可能会得到不同的结果,算法所耗费的时间也不尽相同,这是由算法的特性决定的
sklearn.cluster
sklearn.cluster模块提供的各聚类算法函数可以使用不同的数据形式作为输入
标准数据输入格式:[样本个数,特征个数]定义的矩阵形式
相似性矩阵输入格式:即由[样本数目,样本数目]定义的矩阵形式,矩阵中的每一个元素为两个样本的相似度,如DBSCAN,AffinityPropagation(近邻传播算法)接受这种输入。如果以余弦相似度为例,则对角线元素全为1. 矩阵中每个元素的取值范围为[0,1]
具有代表性的聚类函数
降维
降维就是在保证数据所具有的代表性特征或分布的情况下, 将高维数据转化为低维数据的过程
作用:
数据可视化
作为中间过程, 起到精简数据, 提高其他机器学习算法效率的作用
分类和降维
聚类和分类都是无监督学习的典型任务,任务之间存在关联,比如某些高纬数据的分类可以通过降维处理更好的获得,另外学界研究也表明代表性的分类算法如k-means与降维算法如NMF之间存在等价性,在此我们就不展开讨论了,有兴趣的同学可以参考我们推荐的阅读内容
sklearn和降维
降维是机器学习领域的一个重要研究内容,有很多被工业界和学术界接受的典型算法,截止到目前sklearn库提供7种降维算法
降维过程也可以被理解为对数据集的组成成份进行分解(decomposition)的过程,因此sklearn为降维模块命名为decomposition, 在对降维算法调用需要使用sklearn.decomposition模块
sklearn.decomposition的常用算法
标签:元素 style 基本使用 转化 targe 再计算 目标 组成 数学
原文地址:http://www.cnblogs.com/weihuchao/p/6874683.html