标签:mem 最小 sel 题解 data eve another define dia
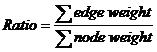
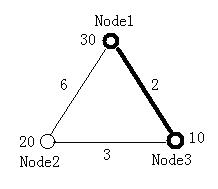
3 2 30 20 10 0 6 2 6 0 3 2 3 0 2 2 1 1 0 2 2 0 0 0
1 3 1 2
题意:求一个稍微变形的“最小生成树”,其值为边权和除以点权和。
题解:用深搜在n个点里选出m个点。再求这m个点的“最小生成树”就可以。
#include <stdio.h>
#include <string.h>
#include <limits.h>
#define maxn 16
int map[maxn][maxn], node[maxn];
int n, m, store[maxn], vis[maxn];
double ans;
bool visted[maxn]; //hash to vis array
double prim()
{
int i, j, u, count = 0, tmp, vnv = 0, vne = 0;
for(i = 1; i <= m; ++i) vnv += node[vis[i]];
memset(visted, 0, sizeof(visted));
visted[1] = 1;
while(count < m - 1){
for(i = 1, tmp = INT_MAX; i <= m; ++i){
if(!visted[i]) continue;
for(j = 1; j <= m; ++j){
if(!visted[j] && map[vis[i]][vis[j]] < tmp){
tmp = map[vis[i]][vis[j]]; u = j;
}
}
}
if(tmp != INT_MAX){
visted[u] = 1;
vne += tmp; ++count;
}
}
return vne * 1.0 / vnv;
}
void DFS(int k, int id)
{
if(id > m){
double tmp = prim();
if(tmp - ans < -(1e-8)){
ans = tmp; memcpy(store, vis, sizeof(vis));
}
return;
}
for(int i = k; i <= n; ++i){
vis[id] = i;
DFS(i + 1, id + 1);
}
}
int main()
{
int i, j;
while(scanf("%d%d", &n, &m), n || m){
for(i = 1; i <= n; ++i) scanf("%d", &node[i]);
for(i = 1; i <= n; ++i)
for(j = 1; j <= n; ++j)
scanf("%d", &map[i][j]);
ans = INT_MAX;
DFS(1, 1);
for(i = 1; i <= m; ++i)
if(i != m) printf("%d ", store[i]);
else printf("%d\n", store[i]);
}
return 0;
}HDU2489 Minimal Ratio Tree 【DFS】+【最小生成树Prim】
标签:mem 最小 sel 题解 data eve another define dia
原文地址:http://www.cnblogs.com/slgkaifa/p/6877805.html