标签:二叉树的高度 pre class 解决 dex 手机号 比较 index 影响
散列表(Hash table)
散列表,是根据关键码值(Key value)而直接进行访问的数据结构。它通过把关键码值映射到表中一个位置来访问记录,以加快查找的速度。这个映射函数叫做散列函数,存放记录的数组叫做散列表。
已知的查找方法:
1.顺序查找 O(N)
2.二分查找(静态查找) O(log2N)
3.二叉搜索树 O(h) h为二叉树的高度
平衡二叉树 O(log2N)
Q:如何快速搜索到需要的关键字?如果关键字不方便比较怎么办?
查找的本质:已知对象找位置
有序安排对象:全序、半序
直接“算出”对象位置:散列
散列查找的两项基本工作:
计算位置:构造散列函数确定关键词的存储位置
解决冲突:应用某种策略解决多个关键词位置相同的情况
时间复杂度几乎是常量O(1) 查找时间与问题规模无关
关键操作:查找 插入 删除
散列(Hashing)的基本思想:
1.以关键词key为自变量,通过一个确定的函数h(散列函数)计算出对应的函数值h(key),作为数据对象的存储地址。
2.可能不同的关键词会映射到同一个散列地址上,即h(keyi) = h(keyj) (当keyi≠keyj),称为”冲突(Collision)”。需要某种冲突解决策略
装填因子(Loading Factor):
设散列表空间大小为m, 填入表中元素的个数时n, 则称α = n/m为散列表的装填因子
散列函数的构造方法:
一个“好”的散列函数一般考虑下列两个因素:
1.计算简单,以便提高转换速度
2.关键词对应的地址空间分布均匀,以尽量减少冲突
数字关键词的构造
1.直接定址法
取关键词的某个线性函数值为散列地址
h(key) = a * key + b (a, b为常数)
如:h(key) = key - 1990
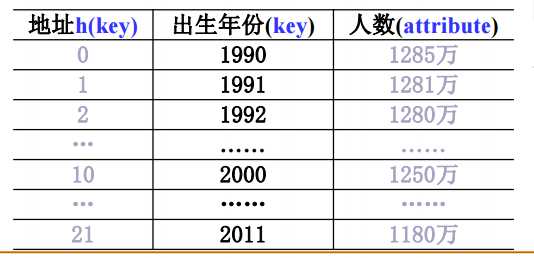
2.除留余数法
h(key) = key mod P
如 h(key) = key % 17 P = Tablesize = 17

一般P取素数
3.数字分析法
分析数字关键字在各位上的变化情况,取比较随机的为作为散列地址
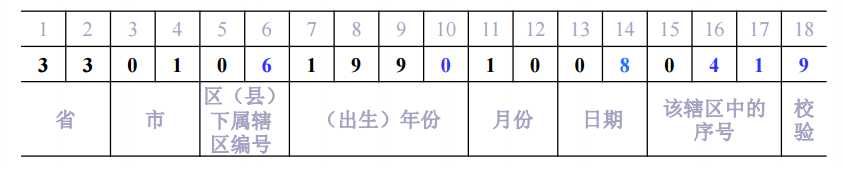
如取11位手机号码key的后4为作为地址: h(key) = atoi(key+7) (char *key)
如果关键词key是18位身份证号码:
h1 (key) = (key[6]-‘0’)*104 + (key[10]-‘0’)*103 + (key[14]-‘0’)*102 + (key[16]-‘0’)*10 + (key[17]-‘0’)
h(key) = h1 (key)*10 + 10 (当 key[18] = ‘x’时)
或 = h1 (key)*10 + key[18]-‘0’ (当 key[18] 为’0’~’9’时)
4.折叠法:
把关键词分割成位数相同的几个部分,然后叠加

5.平方取中法:
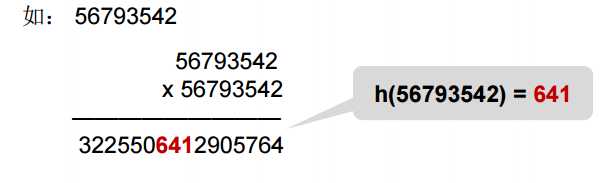
尽量使每一位都对最终结果产生影响
字符关键词的散列函数构造
1.简单的散列函数—ASCⅡ码加和法
h(key) = (Σkey[i]) mod TableSize
冲突严重 如a3, b2, c1, eat, tea
2.简单的改进—前3个字符移位法
h(key)=(key[0]*272 + key[1]*27 + key[2])mod TableSize
27 可能有空格
仍然冲突:string street strong structure.. 并且空间浪费 3000/pow(26, 3) = 30%
3.好的散列函数—移位法
设计关键词的所以n个字符,并且分布很好:
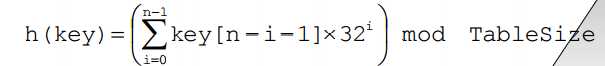
如:h(“abcde”)=‘a’*324+’b’*323+’c’*322+’d’*32+’e’
Index Hash( const char *key, int TableSize ) { unsigned int h = 0; while (*key != ‘\0‘) h = (h << 5) + *key++; return h % TableSize; }
标签:二叉树的高度 pre class 解决 dex 手机号 比较 index 影响
原文地址:http://www.cnblogs.com/whileskies/p/6881377.html