标签:ini 路径 sqrt 自己 == 注意 lowbit 并且 math
树形背包DP。

1 #include <cstdio> 2 3 #define maxn 110 4 #define R register 5 #define cmax(_a, _b) (_a < (_b) ? _a = (_b) : 0) 6 struct Edge { 7 Edge *next; 8 int to; 9 } *last[maxn], e[maxn << 1], *ecnt = e; 10 inline void link(R int a, R int b) 11 { 12 *++ecnt = (Edge) {last[a], b}; last[a] = ecnt; 13 *++ecnt = (Edge) {last[b], a}; last[b] = ecnt; 14 } 15 int f1[maxn][maxn], f2[maxn][maxn], m; 16 bool vis[maxn]; 17 void dfs(R int x) 18 { 19 vis[x] = 1; 20 for (R int i = 0; i <= m; ++i) f1[x][i] = f2[x][i] = 1; 21 for (R Edge *iter = last[x]; iter; iter = iter -> next) 22 if (!vis[iter -> to]) 23 { 24 dfs(iter -> to); 25 for (R int j = m; j; --j) 26 for (R int k = 0; k < j; ++k) 27 { 28 cmax(f1[x][j], f2[x][j - k - 1] + f1[iter -> to][k]); 29 k != j - 1 ? cmax(f1[x][j], f1[x][j - k - 2] + f2[iter -> to][k]) : 0; 30 } 31 for (R int j = m; j >= 2; --j) 32 for (R int k = 0; k < j - 1; ++k) 33 cmax(f2[x][j], f2[x][j - k - 2] + f2[iter -> to][k]); 34 } 35 } 36 int main() 37 { 38 R int n; scanf("%d%d", &n, &m); 39 for (R int i = 1; i < n; ++i) {R int a, b; scanf("%d%d", &a, &b); link(a, b);} 40 dfs(0); 41 R int ans = 1; 42 for (R int i = 1; i <= m; ++i) cmax(ans, f1[0][i]), cmax(ans, f2[0][i]); 43 printf("%d\n", ans); 44 return 0; 45 }
暂时还没做。marked。
做完发现自己推式子和推结论的能力不足。这题有一个结论是只和对角线上的元素的权值有关,并且f[a,b]可以写成k*a*b的形式(这个结论我也是网上看的,但是我向BZOJ要的数据里这个条件并不满足,如果直接将题目给你的x/a/b得到的不会是一个整数,而把x/a/b改成模意义下x*a^(-1)*b^(-1)居然就能过了)。然后推出来是∑f[d]*∑∑(i*j*[gcd(i,j)==d]),然后还有一个结论是
∑i*[gcd(i,n)==1]=phi(n)*n/2。如果知道这两个结论应该剩下就只剩套路了(?)。设g[n] = ∑∑(i*j*[gcd(i,j)==1], 1<=i,j<=n),答案变成求∑f[d]*g[k/d]。然后k/d是根号分段的,根号枚举一下然后动态地求前缀和。前缀和这里用分块来实现根号修改O1查询。总的复杂度O(n+m√n)。

1 #include <cstdio> 2 #include <cmath> 3 4 #define R register 5 #define maxn 4000010 6 #define maxs 2333 7 typedef long long ll; 8 const int mod = 1e9 + 7; 9 int pr[maxn], prcnt, phi[maxn], g[maxn], f[maxn]; 10 int sum[maxn], ssum[maxs]; 11 bool vis[maxn]; 12 inline int qpow(R int base, R int power) 13 { 14 R int ret = 1; 15 for (; power; power >>= 1, base = 1ll * base * base % mod) 16 power & 1 ? ret = 1ll * ret * base % mod : 0; 17 return ret; 18 } 19 int gcd(R int a, R int b) 20 { 21 return !b ? a : gcd(b, a % b); 22 } 23 int main() 24 { 25 R int m, n; scanf("%d%d", &m, &n); 26 phi[1] = 1; g[1] = 1; f[1] = 1; 27 for (R int i = 2; i <= n; ++i) 28 { 29 if (!vis[i]) pr[++prcnt] = i, phi[i] = i - 1; 30 g[i] = (g[i - 1] + 1ll * i * i % mod * phi[i]) % mod; 31 f[i] = 1ll * i * i % mod; 32 for (R int j = 1; j <= prcnt && 1ll * pr[j] * i <= n; ++j) 33 { 34 vis[i * pr[j]] = 1; 35 if (i % pr[j] == 0) 36 { 37 phi[i * pr[j]] = phi[i] * pr[j]; 38 break; 39 } 40 else phi[i * pr[j]] = phi[i] * phi[pr[j]]; 41 } 42 } 43 R int size = sqrt(n), tot = n / size + 1; 44 // printf("\nsize%d\n", size); 45 for (R int i = 1; i <= n; ++i) 46 if (i % size == 0) ssum[i / size] = (ssum[i / size - 1] + sum[i - 1]) % mod, sum[i] = f[i]; 47 else sum[i] = (sum[i - 1] + f[i]) % mod; 48 // for (R int i = 1; i <= n; ++i) printf("%d ", sum[i]); puts(""); 49 for (; m; --m) 50 { 51 R int a, b, k, d; R ll x; 52 scanf("%d%d%lld%d", &a, &b, &x, &k); 53 // if (x % a != 0 || x % b != 0) puts("WA"), printf("%lld %d %d %d\n", x, a, b, m); 54 x %= mod; 55 // printf("kk %lld\n", kk); 56 f[d = gcd(a, b)] = 1ll * x * qpow(1ll * a * b % mod, mod - 2) % mod * d % mod * d % mod; 57 R int spos = d / size + 1; 58 for (R int i = d; i < spos * size; ++i) sum[i] = ((i % size == 0 ? 0 : sum[i - 1]) + f[i]) % mod; 59 for (R int i = spos; i <= tot; ++i) ssum[i] = (ssum[i - 1] + sum[i * size - 1]) % mod; 60 // for (R int i = 1; i <= n; ++i) printf("%d ", sum[i]); puts(""); 61 R int ans = 0; 62 #define query(x) (sum[(x)] + ssum[(x) / size]) 63 for (R int i = 1, j; i <= k; i = j + 1) 64 { 65 j = k / (k / i); 66 ans = (ans + 1ll * (query(j) % mod - query(i - 1) % mod + mod) % mod * g[k / i]) % mod; 67 } 68 printf("%d\n", ans); 69 } 70 return 0; 71 }
挺裸的二维数点问题。扫描线+树状数组简单维护即可。(将一个询问拆成几个前缀询问加加减减的形式)

1 #include <cstdio> 2 #include <algorithm> 3 4 #define R register 5 #define lowbit(_x) ((_x) & -(_x)) 6 #define maxn 100010 7 struct Event { 8 int type, id, x, l, r; 9 inline bool operator < (const Event &that) const {return x < that.x || (x == that.x && type < that.type);} 10 } p[maxn << 2]; 11 int hash[maxn << 2], hcnt, pcnt; 12 typedef long long ll; 13 ll b[maxn << 2], ans[maxn]; 14 inline void add(R int pos, R int val) 15 { 16 for (; pos <= hcnt; pos += lowbit(pos)) b[pos] += val; 17 } 18 inline ll query(R int pos) 19 { 20 R ll ret = 0; 21 for (; pos; pos -= lowbit(pos)) ret += b[pos]; 22 return ret; 23 } 24 int main() 25 { 26 R int n, m, pcnt = 0; scanf("%d%d", &n, &m); 27 for (R int i = 1; i <= n; ++i) 28 { 29 R int x, y, pi; scanf("%d%d%d", &x, &y, &pi); 30 hash[++hcnt] = y; 31 p[++pcnt] = (Event) {1, 0, x, y, pi}; 32 } 33 for (R int i = 1; i <= m; ++i) 34 { 35 R int x_1, y_1, x_2, y_2; scanf("%d%d%d%d", &x_1, &y_1, &x_2, &y_2); 36 hash[++hcnt] = y_1; hash[++hcnt] = y_2; 37 p[++pcnt] = (Event) {2, i, x_1 - 1, y_1, y_2}; 38 p[++pcnt] = (Event) {3, i, x_2, y_1, y_2}; 39 } 40 std::sort(hash + 1, hash + hcnt + 1); 41 hcnt = std::unique(hash + 1, hash + hcnt + 1) - hash - 1; 42 std::sort(p + 1, p + pcnt + 1); 43 for (R int i = 1; i <= pcnt; ++i) 44 { 45 p[i].l = std::lower_bound(hash + 1, hash + hcnt + 1, p[i].l) - hash; 46 if (p[i].type == 1) 47 { 48 add(p[i].l, p[i].r); 49 } 50 else 51 { 52 p[i].r = std::lower_bound(hash + 1, hash + hcnt + 1, p[i].r) - hash; 53 if (p[i].type == 2) ans[p[i].id] -= query(p[i].r) - query(p[i].l - 1); 54 else ans[p[i].id] += query(p[i].r) - query(p[i].l - 1); 55 } 56 } 57 for (R int i = 1; i <= m; ++i) printf("%lld\n", ans[i]); 58 return 0; 59 }
刚开始我连构图都没想到。后来看了题解完构图还是构错了。
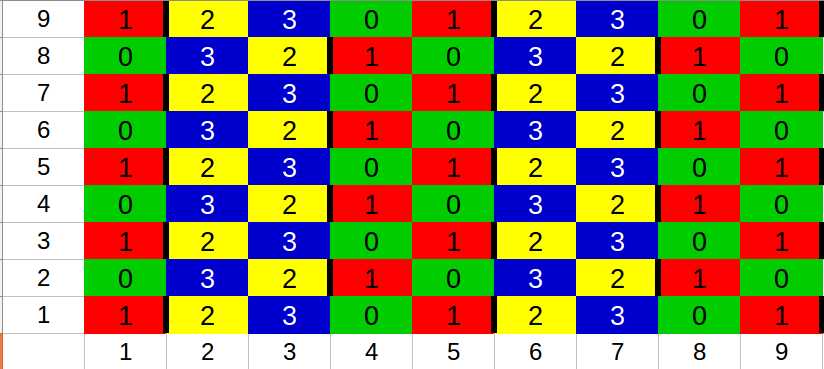
将格子染成如上图所示的四种颜色,然后每一种方块都可以表示成0-1-2-3的形式。然后构建分层图,一条从s到t的路径表示的就是一个弃疗的方块,所以跑一个最小割即可。然后我一开始好像染色还染错了,注意一下染色的顺序(一定得都是0-1-2-3的形式),如果染不清楚的话可能会有奇怪的错误。还有,10w的网络流到底是怎么跑过去的,我不是很能理解啊。。。

1 #include <cstdio> 2 #include <map> 3 #include <algorithm> 4 #include <cstring> 5 6 #define R register 7 #define P std::pair<int, int> 8 #define maxn 200010 9 #define inf 0x7fffffff 10 #define dmin(_a, _b) ((_a) < (_b) ? (_a) : (_b)) 11 std::map<P, int> id; 12 int x[maxn], y[maxn], w[maxn]; 13 struct Edge { 14 Edge *next, *rev; 15 int to, cap; 16 } *last[maxn], *cur[maxn], e[maxn * 10], *ecnt = e; 17 inline void link(R int a, R int b, R int w) 18 { 19 // printf("%d %d %d\n", a, b, w); 20 *++ecnt = (Edge) {last[a], ecnt + 1, b, w}; last[a] = ecnt; 21 *++ecnt = (Edge) {last[b], ecnt - 1, a, 0}; last[b] = ecnt; 22 } 23 int dep[maxn], q[maxn], s, t, ans; 24 inline bool bfs() 25 { 26 memset(dep, -1, (t + 1) << 2); 27 dep[q[1] = t] = 0; R int head = 0, tail = 1; 28 while (head < tail) 29 { 30 R int now = q[++head]; 31 for (R Edge *iter = last[now]; iter; iter = iter -> next) 32 if (iter -> rev -> cap && dep[iter -> to] == -1) 33 dep[q[++tail] = iter -> to] = dep[now] + 1; 34 } 35 return dep[s] != -1; 36 } 37 int dfs(R int x, R int f) 38 { 39 if (x == t) return f; 40 R int used = 0; 41 for (R Edge* &iter = cur[x]; iter; iter = iter -> next) 42 if (iter -> cap && dep[iter -> to] + 1 == dep[x]) 43 { 44 R int v = dfs(iter -> to, dmin(f - used, iter -> cap)); 45 iter -> cap -= v; 46 iter -> rev -> cap += v; 47 used += v; 48 if (used == f) return f; 49 } 50 return used; 51 } 52 void dinic() 53 { 54 while (bfs()) 55 { 56 memcpy(cur, last, sizeof cur); 57 ans += dfs(s, inf); 58 } 59 } 60 void build(R int _x, R int _y, R int i) 61 { 62 R P next; 63 next = std::make_pair(_x, _y); 64 if (id[next]) link(id[next] << 1 | 1, i << 1, inf); 65 } 66 int main() 67 { 68 R int c, r, n; scanf("%d%d%d", &c, &r, &n); 69 for (R int i = 1; i <= n; ++i) 70 { 71 scanf("%d%d%d", &x[i], &y[i], &w[i]); 72 R P pos = std::make_pair(x[i], y[i]); 73 id[pos] = i; 74 } 75 s = 0; t = n * 2 + 2; 76 for (R int i = 1; i <= n; ++i) 77 { 78 R int col = y[i] & 1 ? x[i] % 4 : (x[i] % 4) ^ 1; 79 // printf("x %d y %d col %d\n", x[i], y[i], col); 80 link(i << 1, i << 1 | 1, w[i]); 81 if (col == 0) 82 { 83 link(s, i << 1, inf); 84 } 85 else if (col == 1) 86 { 87 build(x[i], y[i] - 1, i); 88 build(x[i], y[i] + 1, i); 89 build(x[i] + (y[i] & 1 ? -1 : 1), y[i], i); 90 } 91 else if (col == 2) 92 { 93 build(x[i] + (y[i] & 1 ? -1 : 1), y[i], i); 94 } 95 else if (col == 3) 96 { 97 build(x[i], y[i] - 1, i); 98 build(x[i], y[i] + 1, i); 99 build(x[i] + (y[i] & 1 ? -1 : 1), y[i], i); 100 link(i << 1 | 1, t, inf); 101 } 102 } 103 dinic(); 104 printf("%d\n", ans); 105 return 0; 106 }
还没做。marked。
标签:ini 路径 sqrt 自己 == 注意 lowbit 并且 math
原文地址:http://www.cnblogs.com/cocottt/p/6875527.html