标签:类型 表达 常见 操作 image 简单 不能 time 应用
数理统计讨论的问题不一定都是随机现象,比如人口信息的统计、具体数据的测量,它们的结果都是确定的。但实际问题的操作并不是数学所关心的,剥离问题的外壳,这些问题都可以用随机现象来描述,比如人口信息和测量误差都可以用一个正态分布来近似。建立统计的概率模型,正是数理统计区别于广义统计学的关键,为模型定义统一、明确的对象也是任何数学分支的起点。
既然这样,数理统计的研究对象其实还是随机变量,具体问题中所有可能的取值被称为全体,而每一个值称为个体。不同于概率论中研究分布的性质,统计中的分布信息往往是未知的,这样的随机变量习惯写作\(X\)。为了得到\(X\)的更多信息,需要采集它的观察值\(X_1,X_2,\cdots,X_n\),它们称为样本。一般假定\(X_i\)是与\(X\)同分布的独立随机变量,具体样本值则记作\(x_i\)。
统计问题中的主要信息就是样本值\(X_i\),能对它进行的处理只有函数计算\(f(X_1,\cdots,X_n)\),这些函数值被称为样本统计量。统计量不能任意选取,它需要根据实际需要并一般有直观意义。比如最常用的统计量是式(1)中的样本均值\(\bar{X}\)和样本方差\(S^2\),它们一般作为分布的均值和方差的估计值。
\[\bar{X}=\frac{1}{n}\sum\limits_{i=1}^nX_i;\;\;S^2=\frac{1}{n-1}\sum\limits_{i=1}^n(X_i-\bar{X})^2\tag{1}\]
既然样本是随机变量,统计量自然也是随机变量。如果\(X\)的期望和方差是\((\mu,\sigma^2)\),则易知\(\bar{X}\)是有期望\(\mu\)和方差\(\dfrac{\sigma^2}{n}\)的随机变量。不难算得,\(S^2\)的期望值正好是\(\sigma^2\),所有系数取\(\frac{1}{n-1}\)是合理的,\(S^2\)的完整称谓是“修正的样本方差”。我们暂时可以这样“直觉”地解释这个现象:均值\(\bar{X}\)是由\(X_i\)生成的,它会随着\(X_i\)的变动而变动,这就导致真正自由、有效的变量减少了一个。下面马上会回来重新讨论这个问题。
更一般的,比较重要的统计量还有样本原点矩和样本中心距(式(2)),要注意\(k>1\)时,样本中心距都需要修正,只不过在\(n\)很大时可以近似地使用。其中一阶原点矩便是样本均值,二阶中心距便是未修正的样本方差,其它的统计量使用频率不高。
\[a_k=\frac{1}{n}\sum\limits_{i=1}^nX_i^k;\;\;m_k=\frac{1}{n}\sum\limits_{i=1}^n(X_i-\bar{X})^k\tag{2}\]
研究统计量是为了获取分布的信息,我们有一个很朴素的想法:当样本数足够多后,应当能绘制出分布函数\(F(x)\)的图形。根据分布函数的定义特点,可以定义这样一个统计量\(v_n(x)\):它表示满足\(X_i\leqslant x\)的样本数,并记\(F_n(x)=\dfrac{v_n(x)}{n}\),它称为经验分布函数。对于指定的\(x\),\(F_n(x)\)是随机变量,当把\(x\)也看作变量时,我们只好叫\(F_n(x)\)“随机函数”。不过不用担心概念会变复杂,因为\(|F_n(x)-F(x)|\)的最大值才是我们要关心的,而它是一个随机变量。数理统计中有著名的格里文科定理(式(3)),它说明\(F_n(x)\)以概率\(1\)收敛于\(F(x)\)。
\[P\left\{\lim_{n\to\infty}\sup_{x\in\mathbb{R}}\left|F_n(x)-F(x)\right|=0\right\}=1\tag{3}\]
在概率论中我们熟知一个结论:如果\(X_1,\cdots,X_n\)互相不相关,则\(Y=X_1+\cdots+X_n\)的期望、方差可以简单地展开。\(n\)个\(X_i\)对\(Y\)的影响互不相关,这样的统计量十分易于讨论,我们暂且称它的自由度是\(n\)。下面就来研究一下样本方差的自由度为什么是\(n-1\)而不是\(n\),不过在此之前,需要先讨论一下随机变量正交变换的性质。
对互不相关的随机变量\(X_i\),设对它们做正交线性变换后得到\(Y_i\),则首先容易得到式(4)。然后分别展开\(E(Y_iY_j)\)和\(E(Y_i)E(Y_j)\),根据正交性,以及\(X_i\)独立同分布,容易有式(5)成立,所以\(Y_i\)互不相关。这个结论对任何随机变量都成立,且也符合正交变换的一贯性质。
\[(X_1,\cdots,X_n)=(Y_1,\cdots,Y_n)A;\,AA^T=I\;\Rightarrow\;\sum_{i=1}^nX_i^2=\sum_{i=1}^nY_i^2\tag{4}\]
\[E(Y_iY_j)-E(Y_i)E(Y_j)=\sum_{k=1}^na_{ki}a_{kj}(E(X_k^2)-E^2(X_k))=0\tag{5}\]
特别地,式(6)左的\(Y_1\)可以扩展为一个正交变换,利用式(4)便可得到式(6)右的结论。这不仅说明了\(S^2\)的自由度为\(n-1\),还可以知道\(\bar{X}\)和\(S^2\)是不相关的,这个结论非常重要。
\[Y_1=\sqrt{n}\bar{X}\;\Rightarrow\;\sum_{i=1}^n(X_i-\bar{X})^2=\sum_{i=1}^nX_i^2-Y_1^2=\sum_{i=2}^nY_i^2\tag{6}\]
对于满足再生性的随机变量,\(Y_i\)和\(X_i\)具有相同的分布类型,且可知满足式(6)的\(Y_1\)有期望\(\sqrt{n}\mu\)和方差\(\sigma^2\),而其它\(Y_i\)有期望\(0\)和方差\(\sigma^2\)。特别地,当\(X_i\)是正态分布时,可以有式(7)成立,且\(\bar{X}\)与\(S^2\)相互独立。对\(\bar{X}\)的结论,一般写作式(8),右边是一个确定的分布(后面会用到)。
\[X_i\sim N(\mu,\sigma^2)\;\Rightarrow\;Y_1\sim N(\sqrt{n}\mu,\sigma^2);\; Y_i\sim N(0,\sigma^2)\tag{7}\]
\[\dfrac{\sqrt{n}(\bar{X}-\mu)}{\sigma}\sim N(0,1)\tag{8}\]
更一般地,对于自由度为\(n\)的随机变量\(Q=X_1^2+\cdots+X_n^2\),其中\(X_i\)互不相关。现在把\(Q\)看成\(X_i\)的正定二次型,并记行向量\(\vec{X}=[X_1,\cdots,X_n]\)。假设\(Q\)可以分解为\(r\)个半正定二次型之和(式(9)左),且\(Q_k\)的秩\(n_k\)满足\(n_1+\cdots+n_r=n\)。由\(A_k\)的秩为\(n_k\)且半正定可知,存在\(n\times n_k\)的矩阵\(B_k\),使得\(Q_k=\vec{X}B_kB_k^T\vec{X}^T\)。
\[Q=Q_1+\cdots+Q_r=\vec{X}BB^T\vec{X}^T=\vec{Y}\vec{Y}^T\tag{9}\]
令方阵\(B=[B_1,\cdots,B_r]\)和\(\vec{Y}=\vec{X}B\),则有\(Q=\vec{Y}\vec{Y}^T\)(式(9)右),从而\(BB^T=I_n\),\(B\)是一个正交矩阵。因为\(Y_j\)是由\(X_i\)正交变换而来,故根据式(5)知\(Y_j\)互不相关,继而\(Q_k\)之间是互不相关的。值得提醒的是,当\(Q\)也是一般的半正定二次型时,结论仍然成立,这个条件使用起来会更方便,请自行论证。
现在利用这个结论再讨论\(S^2\)的自由度,首先显然有式(10)成立,其中的每一项都是关于\(X_i\)的半正定二次型。当半正定二次型具有形式\(\sum\limits_{i=1}^nZ_i^2\),且\(Z_i\)还有\(r\)个线性约束条件时,它本质上是关于\(n-r\)个自由变量的正定二次型,从而秩为\(n-r\)。这个小结论在判定二次型秩时很有用,比如\(S^2\)中设\(Z_i=X_i-\bar{X}\),则有\(1\)个限制条件\(Z_1+\cdots+Z_n=0\),从而\(S^2\)的秩为\(n-1\)。另外显然式(10)左的秩为\(n\),\(\bar{X}\)的秩为\(1\),满足以上定理的条件,故有\(S^2,\bar{X}\)不相关。
\[\sum_{i=1}^nX_i^2=n\bar{X}^2+(n-1)S^2\tag{10}\]
统计量也是随机变量,各种形式的统计量会产生许多新的随机变量,这些变量中的有些是经常出现的,有必要事先对它们做一些介绍。因为正态分布适用的场合最为广泛,这里的统计学三大分布都是基于正态分布的。
在介绍\(\chi^2\)分布之前,先讨论一个更一般的分布。将埃尔朗分布中的\(r\)扩展为任意正实数,得到的分布(11)称为\(\varGamma\)分布,一般记作\(\varGamma(r,\lambda)\)。式子中的\(\varGamma(r)\)确保了\(p(x)\)为密度函数,它被称为\(\varGamma\)函数。\(\varGamma\)函数在实数域是个\(U\)形函数,它有式(12)的基本结论,由于\(\varGamma(n)=(n-1)!\),它也被看成是阶乘概念的扩展。
\[p(x)=\dfrac{\lambda^r}{\varGamma(r)}x^{r-1}e^{-\lambda x},\;\varGamma(x)=\int_{-\infty}^{+\infty}t^{x-1}e^{-t}\,\text{d}t\tag{11}\]
\[\varGamma(x+1)=x\varGamma(x);\;\;\varGamma(1)=1,\;\varGamma(\dfrac{1}{2})=\sqrt{\pi}\tag{12}\]
\(\varGamma\)分布具有和埃尔朗分布同样的特征函数,并且也满足再生性。这里不打算讨论\(\varGamma\)分布的更多性质,而是关注它的一类特例。假设\(X\sim N(0,1)\),可以证明\(X^2\sim\varGamma(\dfrac{1}{2},\dfrac{1}{2})\),这是个奇妙的巧合!如果\(X_1,\cdots,X_n\)是独立的标准状态分布,利用再生性有式(13)成立,它被称为自由度为\(n\)的\(\chi^2\)(卡方)分布,记作\(\chi_n^2\)。
\[X_i\sim N(0,1)\;\Rightarrow\;\sum_{i=1}^nX_i^2\sim\varGamma(\dfrac{n}{2},\dfrac{1}{2})=\chi_n^2\tag{13}\]
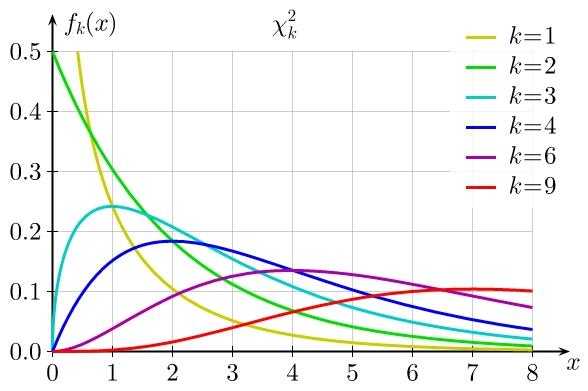
上图是\(\chi^2\)分布的密度函数,\(n=1\)时便是\(X^2\),它有两条渐近线,\(n=2\)时是指数分布,\(n>2\)时分布曲线类似但越来越扁平。容易算得\(\chi_1^2\)有期望\(1\)和方差\(2\),这就得到\(\chi_n^2\)分布的期望和方差(式(14))。继续上面对\(S^2\)的讨论,由于\(Y_i\sim N(0,\sigma^2)\),可以得到\(S^2\)满足式(15)。另外如果\(X\)是指数函数,显然有\(2\lambda X\sim\chi_2^2\)。
\[Y\sim \chi_n^2\;\Rightarrow\;E(Y)=n;\;D(Y)=2n\tag{14}\]
\[\dfrac{(n-1)S^2}{\sigma^2}\sim\chi_{n-1}^2\tag{15}\]
\(\chi^2\)分布的引入无非是为了讨论样本方差的性质,这个分布中不含有任何未知的参数,这种确定的分布非常便于概率的量化计算。但在量化分析的表达式中,不应该含有未知的参数(样本值\(X_i\)、样本容量\(n\)等属于已知量),这样的表达式一般称为枢轴变量。简单说,枢轴变量由已知量组成,且形成一个确定的分布,这个以后会深入讨论。
一般教材上自由度的概念定义在随机变量\(Q=X_1^2+\cdots+X_n^2\)上,其中\(X_i\)是独立的标准正交分布。如果\(Q\)可以分解为\(k\)个半正定二次型,且秩的和为\(n\),则根据前面关于自由度的结论,变换矩阵\(B\)为正交矩阵,从而\(Y_i\)也是互相独立的正交分布。进而\(Q_k\)是自由度为\(n_k\)的卡方分布,且它们互相独立。这个结论称为柯赫伦(Cochran)分解定理,在数理统计中有着非常普遍的应用。
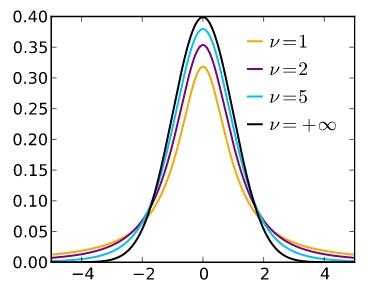
公式(8)中参数\(\sigma\)往往是未知的,这会给分析带来困难,这时可以用\(S\)可以做为\(\sigma\)的近似。令\(X,Y\)分别代表式(8)(15)中的变量,消除\(\sigma\)后就形成变量\(\dfrac{X}{\sqrt{Y/(n-1)}}\)。这应当是我们要关心的数轴变量,它的分布是确定,为了便于讨论研究,需要为它作个定义。一般地,式(16)中的分布被称为自由度为\(n\)的\(t\)分布,记作\(t_n\)。下图是其密度函数,有人已经证明,当\(n\to\infty\)时,\(t\)分布收敛于正态分布,这也是符合直觉的。
\[X\sim N(0,1);\;Y\sim \chi_n^2\;\Rightarrow\;\dfrac{X}{\sqrt{Y/n}}\sim t_n\tag{16}\]
再回到对式(8)(15)的讨论,显然有式(17)成立,这个结论以后经常用到。关于(17)式我想强调一下,式中好像是用\(S\)取代了\(\sigma\),这只是巧合而已,不要忘了其背后原理还是(8)(15)的结合。是因为\(\sigma\)恰巧被消掉才出现了式(17),遇到更复杂的情况时,要重新仔细计算(下一篇将遇到)。
\[\dfrac{\sqrt{n}(\bar{X}-\mu)}{S}\sim t_{n-1}\tag{17}\]
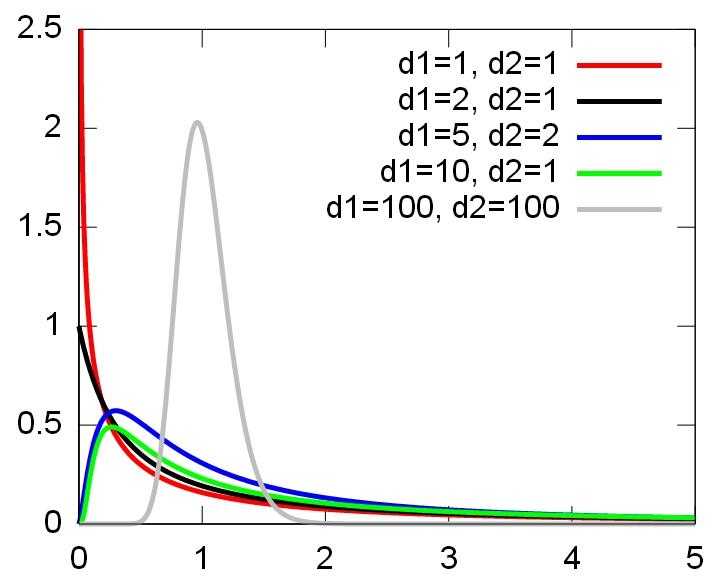
还有一种常见的场景,就是比较两个分布的方差比\(\sigma_1^2/\sigma_2^2\)。同样利用\(S_i^2\)近似\(\sigma_i^2\),并利用公式(15)可以进行类似的讨论。为此,将式(18)中的分布被称为自由度为\(m,n\)的\(F\)分布,记作\(F_{m,n}\),下图是它的密度函数。
\[X\sim\chi_m^2;\;Y\sim\chi_n^2\;\Rightarrow\;\dfrac{X/m}{Y/n}\sim F_{m,n}\tag{18}\]
回到方差的比较,设\(X,Y\)的方差分别为\(\sigma_1^2,\sigma_2^2\),样本容量分别为\(m,n\),样本方差分别为\(S_1^2,S_2^2\),容易知道有式(19)成立。
\[\dfrac{S_1^2}{S_2^2}\cdot\dfrac{\sigma_2^2}{\sigma_1^2}\sim F_{m-1,n-1}\tag{19}\]
数理统计中使用分布函数时,和概率论中是相反的,即根据概率值来确定随机变量的值。满足\(P(X>C)=\alpha\)的\(C\)被称为分布的\(\alpha\)上分位点,对于正态分布和上面的三大分布,\(\alpha\)上分位点分别记作\(u(\alpha),\chi_n^2(\alpha),t_n(\alpha),F_{m,n}(\alpha)\)。其中\(t_n,F_{m,n}\)有式(20)的简单性质,它们在计算和制表中比较有用,证明比较简单,请自行验证。
\[t_n(1-\alpha)+t_n(\alpha)=0;\;\;F_{m,n}(\alpha)\cdot F_{n,m}(1-\alpha)=1\tag{20}\]
标签:类型 表达 常见 操作 image 简单 不能 time 应用
原文地址:http://www.cnblogs.com/edward-bian/p/6888664.html