小Ho:这次的问题好像还是很麻烦的样子啊。
小Hi:没错,小Ho你有什么想法么?
小Ho:我么?我能想到只有枚举啦。因为每一项活动都只有举行和不举行两种状态,因此我直接用O(2^N)的枚举,再对选出来的情况进行计算。最后选出最大的方案。
小Hi:这很明显会超过时间限制吧。
小Ho:我知道啊,那有什么好的方法么?
小Hi:当然有啊,这次我们需要解决的是闭合子图问题。
小Ho:这个闭合子图是啥?
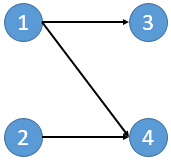
小Hi:所谓闭合子图就是给定一个有向图,从中选择一些点组成一个点集V。对于V中任意一个点,其后续节点都仍然在V中。比如:
在这个图中有8个闭合子图:?,{3},{4},{2,4},{3,4},{1,3,4},{2,3,4},{1,2,3,4}
小Ho:闭合子图我懂了,但是这跟我们这次的问题有啥关系呢?
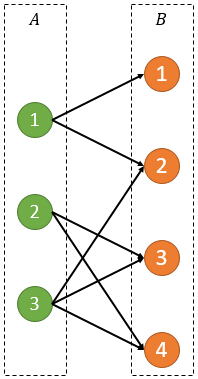
小Hi:我们先把这次的问题转化为2分图。将N个活动看作A部,将M个学生看作B部。若第i个活动需要第j个学生,就连一条从A[i]到B[j]的有向边。比如对于例子:
假如选择A[1],则我们需要同时选择B[1],B[2]。那么选择什么活动和其需要的学生,是不是就刚好对应了这个图中的一个闭合子图呢?
小Ho:你这么一说好像还真是。如果把活跃值算作权值,A部的节点包含有正的权值,B部的节点是负的权值。那么我们要求的也就是一个权值最大的闭合子图了?
小Hi:没错,我们要求解的正是最大权闭合子图。它的求解方法是使用网络流,因此我们需要将这个图再进一步转化为网络流图。
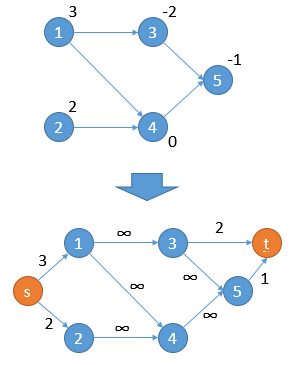
对于一般的图来说:首先建立源点s和汇点t,将源点s与所有权值为正的点相连,容量为权值;将所有权值为负的点与汇点t相连,容量为权值的绝对值;权值为0的点不做处理;同时将原来的边容量设置为无穷大。举个例子:
对于我们题目中的例子来说,其转化的网络流图为:
上图中黑边表示容量无穷大的边。
小Ho:转化模型这一步看上去不是太难,然后呢?
小Hi:先说说结论吧,最大权闭合子图的权值等于所有正权点之和减去最小割。
接下来来证明这个结论,首先我们要证明两个引理:
1. 最小割一定是简单割
简单割指得是:割(S,T)中每一条割边都与s或者t关联,这样的割叫做简单割。
因为在图中将所有与s相连的点放入割集就可以得到一个割,且这个割不为正无穷。而最小割一定小于等于这个割,所以最小割一定不包含无穷大的边。因此最小割一定一个简单割。
2. 简单割一定和一个闭合子图对应
闭合子图V和源点s构成S集,其余点和汇点t构成T集。
首先证明闭合子图是简单割:若闭合子图对应的割(S,T)不是简单割,则存在一条边(u,v),u∈S,v∈T,且c(u,v)=∞。说明u的后续节点v不在S中,产生矛盾。
接着证明简单割是闭合子图:对于V中任意一个点u,u∈S。u的任意一条出边c(u,v)=∞,不会在简单割的割边集中,因此v不属于T,v∈S。所以V的所有点均在S中,因此S-s是闭合子图。
由上面两个引理可以知道,最小割也对应了一个闭合子图,接下来证明最小割就是最大权的闭合子图。
首先有割的容量C(S,T)=T中所有正权点的权值之和+S中所有负权点的权值绝对值之和。
闭合子图的权值W=S中所有正权点的权值之和-S中所有负权点的权值绝对值之和。
则有C(S,T)+W=T中所有正权点的权值之和+S中所有正权点的权值之和=所有正权点的权值之和。
所以W=所有正权点的权值之和-C(S,T)
由于所有正权点的权值之和是一个定值,那么割的容量越小,W也就越大。因此当C(S,T)取最小割时,W也就达到了最大权。
小Ho:我懂了,因为最小割也对应了一个闭合子图,因此它是可以被取得的,W也才能够到达最大权值。
小Hi:没错,这就是前面两条引理的作用。
小Ho:那么最小割的求解就还是用最大流来完成好了!
小Hi:嗯,那就交给你了。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<cstdlib>
#include<queue>
#include<stack>
#include<ctime>
#include<vector>
using namespace std;
int n,m;
struct node
{
int next,to,cap;
}edge[500001];
int head[200001],size=1;
void putin(int from,int to,int cap)
{
size++;
edge[size].next=head[from];
edge[size].to=to;
edge[size].cap=cap;
head[from]=size;
}
void in(int from,int to,int cap)
{
putin(from,to,cap);
putin(to,from,0);
}
int dist[200001],numbs[200001];
void bfs(int src,int des)
{
int i;
queue<int>mem;
mem.push(des);
dist[des]=0;numbs[0]++;
while(!mem.empty())
{
int x=mem.front();mem.pop();
for(i=head[x];i!=-1;i=edge[i].next)
{
int y=edge[i].to;
if(edge[i].cap==0&&dist[y]==0&&y!=des)
{
dist[y]=dist[x]+1;
numbs[dist[y]]++;
mem.push(y);
}
}
}
return;
}
int dfs(int src,int flow,int des)
{
if(src==des)return flow;
int i,low=0,mindist=n+m+2;
for(i=head[src];i!=-1;i=edge[i].next)
{
int y=edge[i].to;
if(edge[i].cap)
{
if(dist[y]==dist[src]-1)
{
int t=dfs(y,min(flow-low,edge[i].cap),des);
edge[i].cap-=t;
edge[i^1].cap+=t;
low+=t;
if(dist[src]>=n+m+2)return low;
if(low==flow)break;
}
mindist=min(mindist,dist[y]+1);
}
}
if(!low)
{
if(!(--numbs[dist[src]]))dist[0]=n+m+2;
++numbs[dist[src]=mindist];
}
return low;
}
int ISAP(int src,int des)
{
int ans=0;
bfs(src,des);
while(dist[0]<n+m+2)ans+=dfs(src,2e8,des);
return ans;
}
int cnt;
int main()
{
//freopen("4.in","r",stdin);
int i,j;
memset(head,-1,sizeof(head));
scanf("%d%d",&n,&m);
for(i=1;i<=n;i++)
{
scanf("%d",&j);
in(m+i,m+n+1,j);
}
for(i=1;i<=m;i++)
{
int a,b,dis;
scanf("%d%d%d",&a,&b,&dis);
in(i,m+a,2e8);
in(i,m+b,2e8);
in(0,i,dis);
cnt+=dis;
}
int maxflow=ISAP(0,n+m+1);
printf("%d",cnt-maxflow);
}