标签:pen 处理 递归 src max lin logs 答案 class
一。概念
线段树是用于处理区间的复杂度为O(log n)一类数据结构。线段树是一棵完美二叉树(区别于完全二叉树)。树上的每个节点维护一个区间,且为父亲节点的区间二等分后的其中一个子区间。
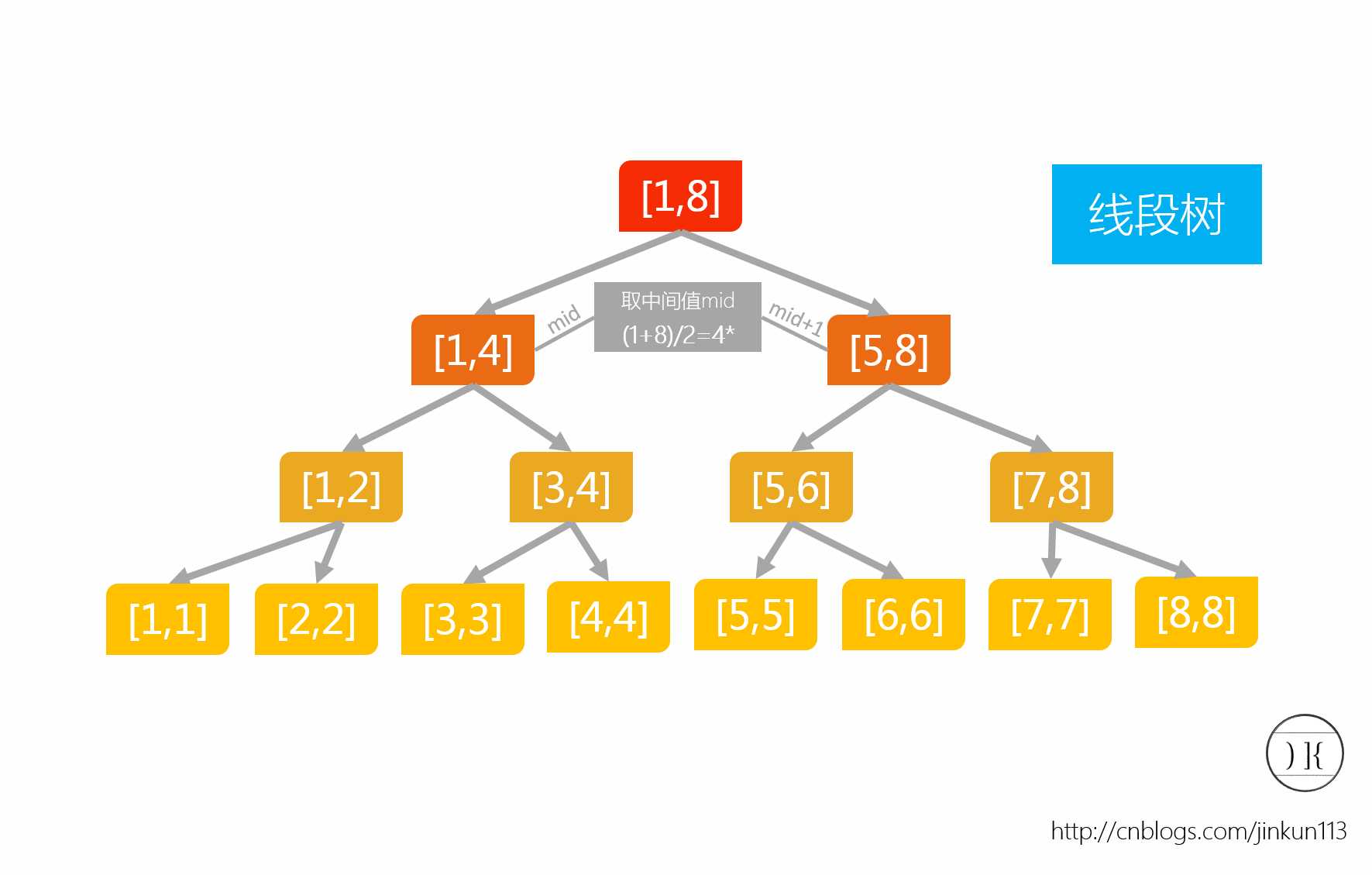
二. 基于线段树的RMQ操作(根据维护的信息不同,线段树还可以实现其他功能)
三. 基于线段树的查询
例如查询区间的最小值
即使查询的是一个比较大的区间,由于较靠上的节点对应较大的区间,通过这些区间就可以知道大部分值中的最小值,从而可以访问较少的节点来求得最小值

1 int n, dat[2 * maxn - 1]; 2 3 void init(int n_) { 4 // 为了简单起见,把元素个数扩大到2的幂次 5 n = 1; 6 while (n < n_) { 7 n *= 2; 8 } 9 for (int i = 0; i < 2 * n - 1; i++) { 10 dat[i] = INF; 11 } 12 } 13 14 // 把第k个值(0 ~ indexed)更新为a 15 void update(int k, int a) { 16 // 叶子节点 17 k += n - 1; 18 dat[k] = a; 19 // 向上更新 20 while (k > 0) { 21 k = (k - 1) / 2; 22 dat[k] = min(dat[k * 2 + 1], dat[k * 2 + 2]); 23 } 24 } 25 26 // 求[a, b]的最小值 27 // 后面的参数时为了方便计算而传入的 28 // k是节点的编号,l, r表示这个节点对应的是[l, r) 左开右闭 29 // 在外部调用时, 用(a, b, k, l, r) 30 31 int query(int a, int b, int k, int l, int r) { 32 //如果[a, b]和[l, r]不相交,则返回一个特殊值 33 if (r <= a || b <= l) return INF; 34 35 //如果[a, b)完全包含[l, r), 则返回当前节点的值 36 if (a <= l && r <= b) return dat[k]; 37 else { 38 int vl = query(a, b, k * 2 + 1, l, (l + r) / 2); 39 int vr = query(a, b, k * 2 + 2, (l + r) / 2, r); 40 return min(vl, vr); 41 } 42 }
标签:pen 处理 递归 src max lin logs 答案 class
原文地址:http://www.cnblogs.com/xFANx/p/6890208.html