标签:总结 不为 src script blog app img http str
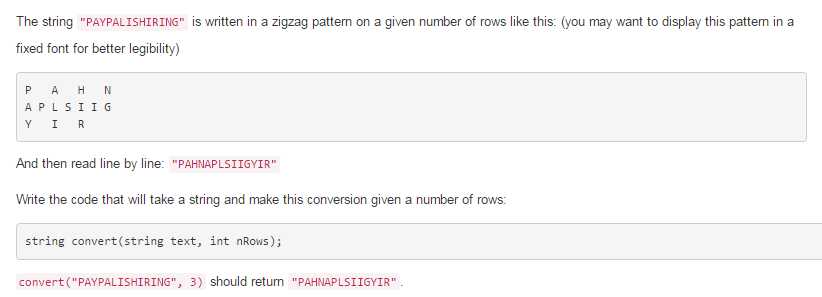
一、Description:
public class Solution { public String convert(String s, int numRows) { } }
二、Solutions:
1、思路:
首先想到按照行来进行添加字符。发现第一行与最后一行位移量为 (numRows-1) * 2; 中间行的第奇数个字符的位移量为上面部分 ,即 step = (numRows-1-j) * 2, 第偶数个字符的位移量为下面部分, 即 2*j。时间复杂度为 O(N^2)。
public class Solution { public String convert2(String s, int numRows) { if (s.length() <= 1 || numRows == 1) return s; int i = 0; // 行数 int step; // 每行位移 int temp; StringBuffer sb = new StringBuffer(); for (int j = 0; j < numRows; j++) { // 处理每一行: step--每一行的位移 i = j; if (j == numRows - 1) // j 为最后一行 step = (numRows-1)*2; else step = (numRows-1-j) * 2; // j 不为最后一行 temp = 1; while(i < s.length()) { // 取每行满足的字符 sb.append(s.charAt(i)); if (temp % 2 == 1) // 如果为行的第奇数个数字,位移为 下面的 step i += step; else if(j != 0 && j != numRows - 1)// 去除边界情况(j 不为第一行且不为最后一行), 位移量为上面的部分,即 2*j i += (numRows - 1) *2 - step; else i += step; temp++; } } return sb.toString(); } }
2、优化:
一列一列的添加。创建StringBuffer数组,按照下标将字符添加到对应的StringBuffer中,最终将StringBuffer进行拼接。图像呈现 上升、下降的形状,用一个标识 flag进行记录。时间复杂度为 O(N)
public class Solution { public String convert(String s, int numRows) { // 一列一列的添加 int len = s.length(); if (len <= 1 || numRows == 1) return s; StringBuffer[] sb = new StringBuffer[numRows]; for (int i = 0; i < numRows; i++) { sb[i] = new StringBuffer(); } boolean flag = true; //判断字符是上升还是下降 int index = 0; //记录下标 int row = 1; //记录行数 while (index < s.length()) { sb[row-1].append(s.charAt(index)); if(flag == true) { row++; if(row == numRows) flag = false; } else { row--; if(row == 1) flag = true; } index++; } for (int i = 1; i < numRows; i++) { sb[0].append(sb[i]); } return sb[0].toString(); } }
三、 总结:
想问题要多方面的思考,想到了按行添加,就可能可以按列添加啊!要注意发散思维!
标签:总结 不为 src script blog app img http str
原文地址:http://www.cnblogs.com/skillking/p/6902395.html