决策树（二）

标签：提升   复杂   不同   ida   http   font   基于   testing   统计   

简介

剪枝（pruning）是指通过移除决策树的某一部分以减少树的大小，被移除的部分的分类能力比较弱，从而降低最终分类器的复杂度，提高泛化能力。

从上一篇文章中，我们知道决策树是通过递归算法产生，然而这可能会出现过拟合（overfitting），也就是，一味的拟合已知的训练数据集，可能会导致分类器过于复杂，对未知的数据分类并不准确。问题是最终的分类决策树的最优大小应该是什么。树越大则越复杂导致过拟合，而树越小的话则可能会忽略掉样本空间中比较重要的结构信息。其实，很难确定在构造决策树的时候，增加一个节点是否会提高分类能力，降低错误率。这就是著名的horizon effect。通常的策略就是构造决策树之后然后进行剪枝以移除那些不重要的节点。

剪枝减小了决策树的大小，但没有降低分类器的准确性（准确性可以由交叉验证集cross-validation set测得）。

方法

剪枝可以分为两类，

• 预剪枝(pre-pruning)，在树增长到能完美的对训练数据集分类之前，就停止树的增长
• 后剪枝(post-pruning)，在树增长到能完美的对训练数据集分类之后，对树进行剪枝

后剪枝在实际应用中能获得更大的成功，因为预剪枝过程中很难判断什么时候停止树的增长。

剪枝中的重要一步是定义一个标准以决定最终的树大小，可以使用如下几种方法，

1. 使用一个没有重复数据点的数据集（来自训练数据集），这个数据集称为验证数据集，使用验证数据集来计算剪枝掉的节点的影响
2. 使用训练数据集创建树，然后使用统计测试来估计是剪掉还是扩展一个节点可能会提升分类性能，这样的统计测试通常有
   a)错误估计Error estimation
   b)Significance testing
3. 最小描述长度原则(minimum description length principle)：使用明确的方法来测量训练数据集和决策树的复杂度，并在在size(size(tree) + size(misclassifications(tree))最小时停止树的生长。

第一种方法最常用，其中，数据集被分为训练数据集和验证数据集，训练集用于构造决策树，而验证集评估剪枝后决策树的性能。下面介绍几种具体方法。

• 误差降低剪枝(REP, Reduced error pruning)，这种方法相对比较简单。自下而上，对每一个非叶节点，此节点上有N_t个样本数，尝试将其替换为一个叶节点，分类改为Nt个样本中分类最多的那个分类值，这样就生成一个简化的树，如果分类的准确性没有降低（在验证数据集上，与替换节点之前的树相比较），则决定替换这个节点为叶节点，否则遍历其他非叶节点，直到遍历结束，最终得到的简化树就是剪枝后的决策树。
• 悲观剪枝(PEP, Pessimistic Error Pruning)，与误差降低剪枝不同，不需要额外的验证数据集。

REP

将所有已知的数据集分一部分用于验证。在训练过程中不使用验证集数据。训练完成后，使用验证集进行测试。剪枝如下：自下而上，自左向右，首先从邻近叶节点的的一个内部节点开始，将此节点替换为叶节点，节点的分类为这个内部节点覆盖到的（训练数据集中）数据点中分类最多的那个分类，使用验证集，如果剪枝后的树的误差率比剪枝前的小，则执行本次剪枝。

REP是最简单的后剪枝方法之一，不过在数据量比较少的情况下，REP方法较少使用，因为训练数据集合中的特性在剪枝过程中被忽略，而事实上这些特性往往确实会影响分类结果。

Statistical Pruning

基于统计置信估计。这种方法的优势是不需要验证数据集，从而所有已知的数据集均可作为训练数据集。

置信区间(Confidence intervals)

 统计剪枝的核心是计算错误率置信区间。对N个训练数据集而言，测量可观测到的错误率为f，然后希望能估计真实的错误率p，注意p是针对所有的输入空间实例而言，而f是对样本（训练数据集）而言。

这里可以类比N次抛硬币，对某一次分类错误而言就类似抛一次硬币正面朝上，错误率就是正面朝上的概率p，显然这是一个（0-1）分布，我们知道期望和方差为

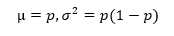  (1)

测量观测样本的错误率 f 就是 

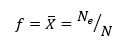           (2)

其中N_e为样本中分类错误个数。根据统计学知识，X ?  是 期望 μ 的无偏估计，且

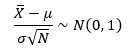        (3)

其中N(0,1)为标准正态分布，根据置信区间的定义，假设我们要得到 1-α 的置信水平，只要(3)式的标准正态分布满足

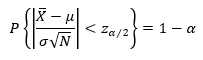  (4)

所以要求的就变成

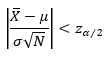            (5)

其中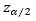对应如下图

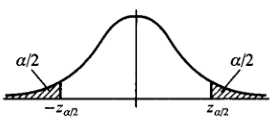
查正态分布概率表可知

 将(1)代入(5)得到

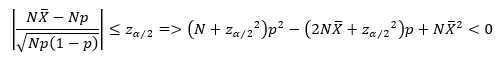    (6)

置信下限和上限分别为

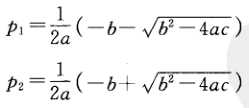
其中，

补充：

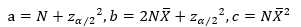
参考³ 里面计算置信区间跟上面不一样，计算如下，

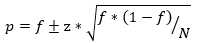   (7)

也就是将根号里面的p替换为f ，也就是将σ 替换为σ‘=sqrt(f*(1-f))。

而我根据概率论与数理统计知识，

样本方差S²为

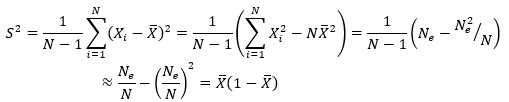     (8)

N足够大时，约等号成立。

X_i为样本空间的随机变量，这里指训练数据集中某一个数据点分类是否错误，如错误则X_i值为1，否则为0。

S²是σ²的无偏估计，

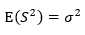
可以将σ 替换为S，则（为什么是 t 分布，可以参考概率论与数理统计课本）

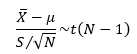
由于样本数量N已知，故 t 分布不依赖任何未知参数，类似地，要获得置信水平1-α，则需要

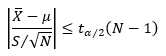                              (9)

t分布如下图，

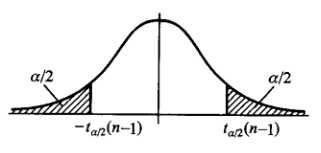
 将(8)代入(9)得到，

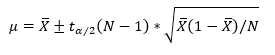      (10)

此即(7)式，其中 z 为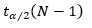，f 为 X ? ，然后 参考³ 里面z是标准正态分布，而这里是 t 分布，但是， 样本数量N足够大时，t 分布近似 标准正态分布 N(0, 1)。

基于置信区间的剪枝

 为了决定是否将非叶节点（包含括其子节点）替换为一个叶节点，C4.5比较了剪枝前后的两个树的置信上限（对错误率的估计），并选择置信上限低的那颗树。剪枝前的非叶节点的错误率估计上限是由其子节点的置信上限的加权平均得到。

例如剪枝前的子树为：

                        wage increase?
                <=2.5 /         \ > 2.5
                     /                           work hours
           <=36 /       \ >36
               /                                 health plan
                none /    half |   full                     /          |                         4+ 2-        1+ 1-      4+ 2-

 现在需要判断 health plan是否需要替换为叶子节点。首先计算三个子节点的错误率上限（4+ 2- 表示4个判断正确，2个判断错误）

        for health plan = none leaf node:
                f = 2/6, N=6 => upper p estimate = .46
                (using z=0.69 for 75-th percentile estimate)

        for health plan = half leaf node:
                f = 1/2, N=2 => upper p estimate = .74

        for health plan = full leaf node:
                f = 2/6, N=6 => upper p estimate = .46

        average upper error rate over the three leaves: .55

（ 这里权重均为1，使用(*)计算置信区间）

另一方面，如果替换为叶节点，则错误率上限为

        f = 5/14, N=14 => upper p estimate = .49

比0.55小，所以health plan节点被剪枝。

PEP

悲观错误剪枝与上面统计剪枝类似，主要是添加了一个修正因子。

假设：

决策树为T，其中非叶节点为T₁，叶节点为T₂

T_t为某一子树，对应的根节点为邻近叶节点的内部节点，子树中某一叶结点t，其覆盖的样本数为n_t，对应的分类为k，那么n_t样本中分类不是k的样本数位et，即 t 节点的错误数，错误率即为 r_t = e_t/n_t，而

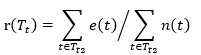    (11)

其中T_t2为T_t中的所有叶节点。

将叶节点t覆盖的n_t个样本整体而言，看作二项式分布，对应的随机变量X为分类错误次数，每个样本判断错误的概率为p，均值和方差分别是

u = np                                  (12)

σ²= np(1-p)                          (13)

对T_t子树而言，剪枝后误判率会增加，这是因为剪枝后只剩一个节点，一个节点只能表示一种分类，通常来说，这会使得误差增加，而误差增加自然就不会剪枝，达不到我们希望剪枝的目的，所以我们加入一个修正因子0.5（或者说惩罚因子），使得每个叶节点的误差数为e_t+0.5。此时误差率为r_t = (e_t+0.5)/n_t，所以

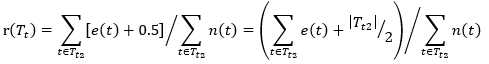       (14)

为什么说剪枝使得误差数增加呢？比如

                        health plan
                none /    half | 
                    /          |     
                4+ 2-        2+ 1-     
 

假设左子节点表示的分类为yes，右子节点肯定与左子节点分类不同，否则就没必要分左右两个子节点了，则右节点分类为no。那么health plan子树中，有4+1个样本分类为yes，2+2个样本分类为no，剪枝后health plan变为叶节点，表示分类为yes，则错误数为4，而剪枝前两个子节点错误数之和为2+1，所以剪枝使得误差数增加。也可以这么想，同样的样本子集，如果用子树分类可以分成多个类，而用单颗叶子节点来分的话只能分成一个类，多个类肯定要准确一些。另外一方面，决策树T 是由训练集生成的，现在又要用训练集来估计分类错误率，自然是不准的，实际错误率肯定要比使用训练数据集检测得到的错误率大些（因为此决策树尽可能完美的匹配训练数据集，包括训练数据集中的一些噪声点也考虑进去了，就导致实际的错误率会大些），一般增加0.5作为修正，至于为什么是0.5后面再介绍。

好了，说了这么多，就是想为 增加0.5 这个修正因子 给个说法，针对目前训练数据集，子树T_t的误差率由(14)给出，假设剪枝后变成一个叶节点，在训练数据集上的误判数为J，同样地，需要增加一个修正因子0.5，变成 J+0.5，由于训练数据集在这个子树上分配的样本在剪枝前后不变，所以我们忽略(14)中的分母，即节点上的样本总数，不考虑错误率，改为考虑错误数，所以是否剪枝的判断依据就取决于 J + 0.5 在不在 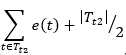 的标准误差内，如果在，则进行剪枝（即使 J+0.5 有可能比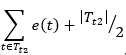大一点点也没事，毕竟还在标准误差内嘛，而且剪枝后使得树变简单了，这正是我们的目的）。

根据上面的讨论，可以将一次分类错误看成0-1分布（当然也可以是其他分布），即，分类错误为1，分类正确为0，n次分类就是二项式分布，对于训练数据集，被考察的子树将对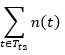 个样本进行分类，根据(12), (13)式，分类错误数（样本期望）和标准误差（样本标准方差）分别为

               (15)

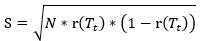        (16)

其中r(T_t)由(14)式给出。

 剪枝后，训练数据集到达此叶节点的数据点不变，分类错误个数为 J+0.5，

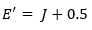                            (17)

如果下式满足，则执行剪枝

 E‘ < E + S                            (18)

当然了，剪枝后成为叶节点的分类选择与前面一样，使用子树所覆盖到的样本中分类最多的那个分类（E‘ 最小）。悲观错误剪枝一般是使用自顶向下，这是因为如果采用自底向上，那么某一子树剪枝后成为新的叶节点后，再向上剪枝，就失去了原来子树中的叶节点的分类信息，而自顶向下时，就是先看较大的子树是否需要剪枝，如果不需要，再向下看较小的子树是否需要剪枝，这样就保证了子树的叶节点信息没有丢失。而前面基于置信区间统计剪枝，显然也很适合自顶向下，至于是否可以自底向上，可以实际试试，个人倾向于自顶向下。

ref

1. 维基百科
2. 统计学习方法，李航
3. statPruning.html
4. 概率论与数理统计

决策树（二）

标签：提升   复杂   不同   ida   http   font   基于   testing   统计   

原文地址：http://www.cnblogs.com/sjjsxl/p/6898512.html