标签:空格 下坡路 line 说明 href 最大 blog 起点 程序
【题面】
为了能在下一次跑步比赛中有好的发挥,贝茜在一条山路上开始了她的训练。贝茜希望能在每次训练中跑得尽可能远,不过她也知道农场中的一条规定:奶牛独自进山的时间不得超过M秒(1< =M< =10,000,000)。
整条山路被贝茜划分成T个长度相同的小段(1< = T< = 100,000),并且,贝茜用S_i表示第i个小段的路况。S_i为u,f,d这3个字母之一,它们分别表示 第i个小段是上坡、平地,或是下坡。
贝茜要花U秒(1< =U< = 100)才能跑完一段上坡路,跑完一段平地的耗时是 F秒(1 < = F < = 100),跑完一段下坡路要花D秒(1 < = D < = 100)。注意,沿山路原路返回的时候,原本是上坡路的路段变成了下坡路,原本是下坡路的路段变成了上坡路。
贝茜想知道,在能按时返回农场的前提下,她最多能在这条山路上跑多远。
输入
第1行: 5个用空格隔开的整数:M,T,U,F,以及D
第2..T+1行: 第i+1行为1个字母S_i,描述了第i段山路的路况
输出
输出1个整数,为贝茜在按时回到农场的前提下,最多能跑到多远
样例输入
13 5 3 2 1
u
f
u
d
f
样例输出
3
提示
贝茜跑步的最大耗时为13秒(这么短...),她跑步的山路一共被划成5段。贝茜跑完一段上坡路的耗时为3秒,平地为2秒,下坡路为1秒。山路各段的走向如下图所示:
/ _ / \ _(让我改一下,真的看不下去误导新手!)
贝茜跑完山路的前3段,然后返回,总耗时为3 + 2 + 3 + 1 + 2 + 1 = 12秒,只比她能在外面呆的时限少1秒。如果她跑得更远,就无法按时回到农场。
【题解】
先对样例画一张草图,如右图:
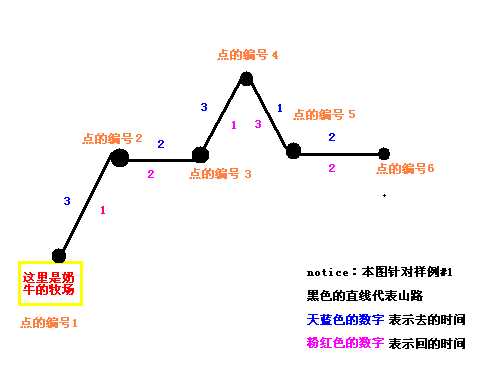
用画图画的,质量不是很好但足以说明问题
已经清楚的表示了这一整幅图,
我们知道,奶牛的出发点一定是在牧场
但是题目没有说牧场在哪里,坑了一会,
最后发现,牧场就是编号为1的点。
容易发现,奶牛在牧场的时间和为0+0=0
在这里第一个加数表示去的时间,
第二个加数表示回的时间,下面也是如此;
简略的记为i=1,time[1]=0+0=0;
同理可求 i=2,time[2]=3+1=4 i=3,time[3]=5+3=8 i=4,time[4]=8+4=12
i=5,time[5]=9+7=16 i=6,time[6]=11+9=20
发现第一个加数是以去的时间累加的,第二个加数是以回来的时间累加的。
算法就出来了!
用tot1[i](1<=i<=t+1)表示第i个点去的时间;
tot2[i](1<=i<=t+1)表示第i个点回的时间;
time[i]=tot1[i]+tot2[i]; 然后扫一遍出即可
但是在比较输出的时候我们通常会采用
for i:=1 to t+1 do begin
time:=tot1[i]+tot2[i];
if time>m then
关键是方框里的输出语句怎么填?
填writeln(i-2)还是writeln(i-1)还是writeln(i) ?
注意了,我们一旦time>m 是表示这步路是不可以走的,需要减一,但是起点到起点不算走一步,所以又减一,一共减二,所以这里输出的是writeln(i-2)!
标签:空格 下坡路 line 说明 href 最大 blog 起点 程序
原文地址:http://www.cnblogs.com/ljc20020730/p/6916822.html