标签：chess   log   之间   算法   img   公约数   约数个数   logs   最大   

20170529-3数论_gcd

1.LCM Range最小公倍数

【题目描述】给定first和last，求所有从first到last的整数的最小公倍数。一些正整数数的最小公倍数指的是，最小的可以被所有这些数整除的正整数。

【输入文件】两个整数，first和last。(1<=first<=last<=12)。

【输出文件】一个整数，表示最小公倍数。

【输入样例】4 5

【输出样例】20

2.最大公约数(gcd.pas/c/cpp)

来源：NOI 2012 chess

【试题描述】有 N 个整数，kAc 会对它们做 Q 次修改。每次修改指的是对所有数加一个整数(可正可负)

每修改一次后，他想知道当前所有数的最大公约数是多少。

【输入格式】第一行两个整数 N, Q

接下来 N 行，每行一个整数，表示这 N 个数的初始值。

接下来 Q 行，每行一个整数，表示这 Q 个操作。第 i 个数表示这一次操作是增加了多少。

【输出格式】共 Q 行，表示进行完第 i 次操作后，所有数的最大公约数。

【输入样例】

3 2

1 -5 7

-1

1

【输出样例】

6

1

【数据规模】

对于 40%：N, Q <= 1000

对于 70%：N, Q <= 40000

对于 100%：N, Q <= 100000，所有数的绝对值始终小于等于 10^16

在这里，我们认为任意非负整数 x 跟 0 的最大公约数都是 x。

3.约数统计AHOI2005

【问题描述】求1..N所有数的所有不同约数个数的和，答案对(10^9+7)取模。

例如N=4

1：1

2：1、2

3：1、3

4：1、2、4

所以答案=1 2 3 4

【样例输入】4

【样例输出】8

【数据范围】

20%：N<=100

40%：N <= 10^4

100%：N <= 10^7

4.最轻的天平 (mobile.c/cpp/pas)L1961

【题目描述】天平的两边有时不一定只能挂物品，还可以继续挂着另一个天平，现在给你一些天平的情况和他们之间的连接关系，要求使得所有天平都能平衡所需物品的总重量最轻，一个天平平衡当且仅当“左端点的重量*左端点到支点的距离=右端点的重量*右端点到支点的距离”。注意题目中的输入保证这些天平构成一个整体。

【输入文件】第一行包含一个n（n<=100），表示天平的数量，天平编号为1到n，接下来包含n行描述天平的情况，每行4个整数p,q,r,b；p和q表示横杆上支点到左边的长度与到右边的距离的比例为p:q，r表示右边的悬挂情况，如果b=0表示右边悬挂的是物品，否则右边悬挂着天平b。

对于所有的输入，保证w*l<2³¹,其中w为最轻的天平重量，而l为输入中描述左右比例时出现的最大值。

【输出文件】输出一个整数表示使得所有的天平都平衡所需最轻的物品总重量。

【样例输入】

4

3 2 0 4

1 3 0 0

4 4 2 1

2 2 0 0

【样例输出】

40

【提示与注意】

对于样例的图：

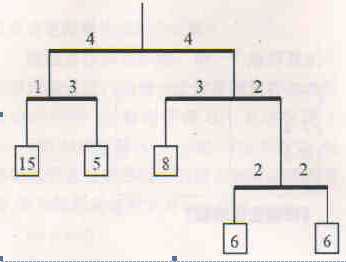
注意：w*l<2^31。

【基础数论】20170529_3 数论_gcd

标签：chess   log   之间   算法   img   公约数   约数个数   logs   最大   

原文地址：http://www.cnblogs.com/ljc20020730/p/6919031.html