标签：com img center 分享 拓展 0.00 tla new 结果
一、实验原理
二、实验步骤
三、实验过程
1.(程序)
（1）二分法：求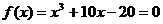 
在区间（1，2）之间的根，取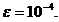
（a）bipart.m:
function [x,m]=bipart(fun,a0,b0,tol)
a=a0;b=b0;
m=1+round(round(log((b-a)/tol))/log(2));
for k=1:m
p=(a+b)/2;
if fun(p)*fun(b)<0
a=p;
else
b=p;
end
x=p;
end
end
(b)fun1.m:
function f=fun1(x) f=x^3+10*x-20;
（2）不动点迭代法：求方程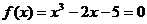
在
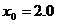附近的根，取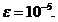
（a）budong.m:
function [x,k]=budong(fun,x0,tol,m)
for k=1:m
x=fun(x0);
if abs(x-x0)<tol
break;
end
x0=x;
end
x=vpa(x,8);
(b)fun.m
function t=fun(x1) syms x; f=x^3-2*x-5; s=subs(diff(f,x),x,x1); x=x1; f=x^3-2*x-5; t=x-f/s;
（3）牛顿迭代法：求方程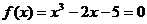
在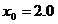
附近的根，取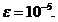
newton.m:
function x1=newton(t1,esp,m)
syms x;
fun=x^3+2*x-5;
for k=1:m
if abs(subs(diff(fun,‘x‘),x,t1))<esp
x1=t1;
break;
else
if subs(diff(fun,‘x‘,2),x,t1)==0
break;
disp(‘解题失败！‘)
else
t0=t1;
t1=t0-subs(fun,x,t0)/subs(diff(fun,‘x‘),x,t0);
if abs(t1-t0)<esp
x1=t1;
break;
end
end
end
end
x1=vpa(x1,8);
2.(运算结果)
（1）二分法：
>> [x,m]=bipart(@fun1,1,2,0.0001)
x =
1.5945
m =
14
(2)不动点迭代法：
>> [x,k]=budong(@fun,2,1e-5,100)
x =
2.0945515
k =
4
(3)牛顿迭代法：
>> x1=newton(2,1e-4,20)
x1 =
1.3282689
3.(拓展（方法改进、体会等）)
对于方程的根为重根的情形，newton法求重根只是线性收敛，迭代缓慢，如果对于求重根的情形，对newton法进行改进，取
，
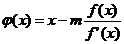则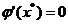 
。用迭代法
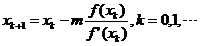
求m重根，则具有二阶收敛性，但要知道的重数m。
计算方程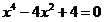
的根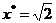
是二重根，用newton法与改进方法求根。
源程序：
newton_biroot.m:
function t=newton_biroot(x1) syms x; f=x^4-4*(x^2)+4; s=subs(diff(f,x),x,x1); x=x1; f=x^4-4*(x^2)+4; t=x-f/s;
biroot1.m:
function t=biroot1(x1) syms x; f=x^4-4*(x^2)+4; s=subs(diff(f,x),x,x1); x=x1; f=x^4-4*(x^2)+4; t=x-2*f/s;
budong.m:
function [x,k]=budong(fun,x0,tol,m)
for k=1:m
x=fun(x0);
if abs(x-x0)<tol
break;
end
x0=x;
x=vpa(x,8)
end
x=vpa(x,8);
运行结果：取初值为2
|
k |
xk |
newton法 |
改进方法 |
|
1 |
x1 |
1.75 |
1.5 |
|
2 |
x2 |
1.5982143
|
1.4166667
|
|
3 |
x3 |
1.5115099
|
1.4142157
|
|
4 |
x4 |
1.4644275
|
1.4142157
|
计算4步，改进方法就已经收敛，而newton法只是线性收敛，要达到同样精度需迭代17次。
附结果：
>> [x,k]=budong(@biroot1,2,1e-5,3)
x =
1.5
x =
1.4166667
x =
1.4142157
x =
1.4142157
k =
3
>> [x,k]=budong(@biroot1,2,1e-5,10)
x =
1.5
x =
1.4166667
x =
1.4142157
x =
1.4142136
k =
4
>> [x,k]=budong(@newton_biroot,2,1e-5,50)
x =
1.75
x =
1.5982143
x =
1.5115099
x =
1.4644275
x =
1.439751
x =
1.4270955
x =
1.4206836
x =
1.4174559
x =
1.4158366
x =
1.4150256
x =
1.4146197
x =
1.4144166
x =
1.4143151
x =
1.4142643
x =
1.414239
x =
1.4142263
x =
1.4142199
k =
17
MATLAB用二分法、不动点迭代法及Newton迭代（切线）法求非线性方程的根
标签：com img center 分享 拓展 0.00 tla new 结果
原文地址：http://www.cnblogs.com/kailugaji/p/6920975.html
