Mooc数据结构-03树

标签：解决   完全   操作方法   事物   链式   二叉树   排列   管理   str   

1 树和树的表示

　　在客观世界中有许多事物存在层次关系

　　如: 人类社会的家谱; 社会的组织结构; 图书信息管理等等

　　分层次组织在管理上有更高的效率

　　数据管理的基本操作之一: 查找

　　　　查找: 根据某个给定的关键字K, 从集合R中找出关键字与K相同的记录

　　　　静态查找: 集合中的记录是固定的, 没有插入和删除操作

　　　　动态查找: 集合中的记录是动态变化的, 可以查询, 插入和删除

　　静态查找

　　　　方法1:顺序查找

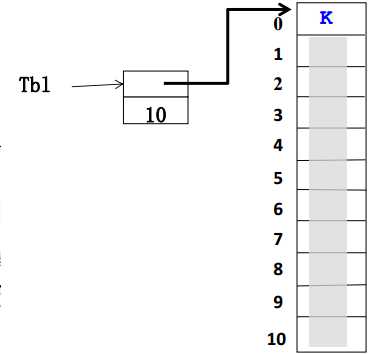
　　　　Tb1指向一个存储空间, 有两部分内容, 一个是指向数组, 另一个是表中数据的个数

　　　　一般把数组首或者尾作为哨兵, 用于减少一次循环终结的判断

　　　　时间复杂度为O(n)

　　　　方法二: 二分查找

　　　　条件: 元素是有序排列的, 用数组来存储

　　　　对N每次除以2直到N变为1, 因而时间复杂度为O(logN) 

　　对于序列1~11, 根据二分查找的提示, 可以形成判定树

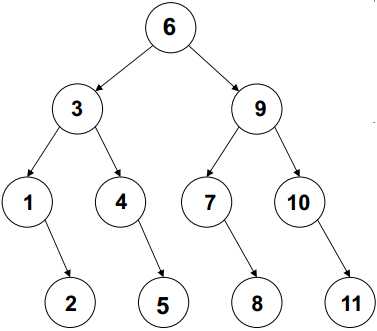
　　判定树上的节点查找到的比较次数刚好是节点所在的层数

　　查找成功的查找次数 <= 判定树的深度

　　n个节点的判定树的深度为 [long₂n]+1 (向下取整再加1)

　　平均成功查找次数ASL = (层数*层所在的节点个数)求和/总结点数

　　　　ASL = (4*4+4*3+2*2+1)/11=3

1.1 树的定义

　　树: n个节点构成的有限集合

　　　　当n=0时, 为空树

　　非空树的性质:

　　　　根root, 用r表示

　　　　其余节点可分为m个互不相交的有限集合, 其中每个集合本身又是一棵树, 叫做原来树的子树

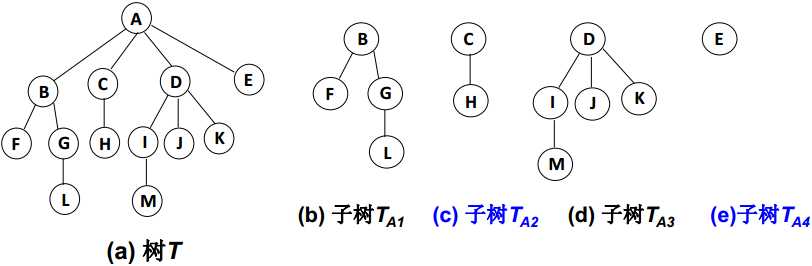
　　　　子树是不相交的

　　　　除了根节点, 每个节点有且仅有一个父节点

　　　　一棵树N个节点的树有N-1条边

　　　　树是保证节点连通的最小的连接方式

　　树的基本术语

　　　　结点的度: 结点的子树的个数

　　　　树的度: 树的所有结点中最大的度数

　　　　叶结点: 度为0的结点(没有子树)

　　　　父结点: 若A有子树, 则A是子树的根节点B的父结点

　　　　子结点: 孩子结点, B就是A的子结点

　　　　兄弟结点: A有多个子树, 子树1的根节点B, 子树2的根节点C, 那么B和C就是兄弟结点

　　　　路径和路径长度: 结点到结点的路径, 路径所包含的边的个数就是长度

　　　　祖先节点: B的父节点A的父节点以及它的父节点, 到根为止都是B的祖先结点

　　　　子孙结点

　　　　结点的层次: 规定根结点的层次为1层

　　　　树的深度: 树的最大层次

1.2 树的表示

　　首先由于树的结构比较复杂, 有父子关系需要存储, 因此不采用数组的方式存储树

　　一般的, 采用链表的形式来存储树

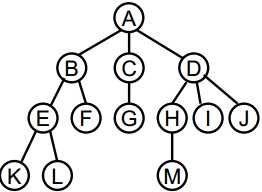
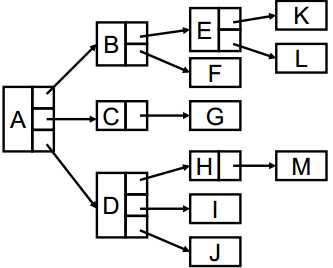
　　这样的结构虽然表明了树, 但是由于每个节点的数据结构不统一, 需要改进

　　(1) 孩子兄弟表示法

　　结构中有两个指针域, 一个指向第一个孩子, 另一个执行相邻的兄弟

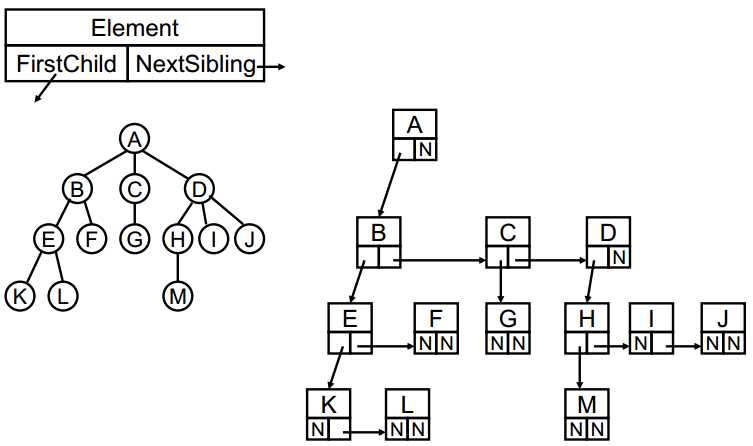
　　对于n个结点, 有2n个指针域, 有n-1条边, 因此空余的指针域为(2n-n+1)=n+1

　　对于这样的表示方式, 如果顺时针旋转45度, 也是一个树的样子, 这个样子就是二叉树

　　二叉树是度为2的树

　　一般地解决二叉树的问题能够解决树的很多问题, 二叉树是树研究的重点

2 二叉树及其存储结构

2.1 二叉树的定义和性质

　　(1) 二叉树的定义

　　二叉树:一个有穷的结点集合

　　　　这个集合可以为空

　　　　若不为空, 则它由根节点和其左子树和右子树两个不相交的二叉树组成

　　二叉树可以被理解为区分左右顺序的度为2的树

　　二叉树的五种基本形态

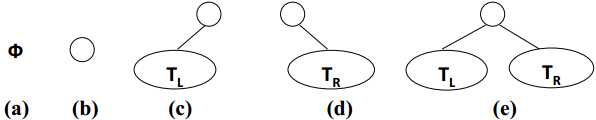
　　(2) 特殊二叉树

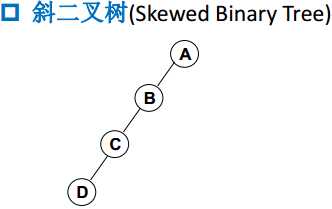
　　只有左子树或者只有右子树

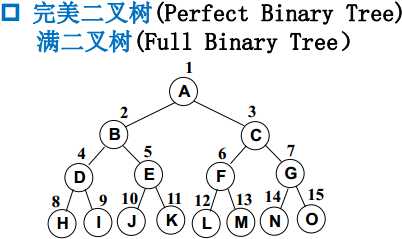
　　也就是说, 完全二叉树只要是在编号上都能在完美二叉树上对应, 就是完全二叉树

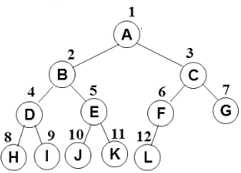
　　(3) 二叉树的性质

　　第i层最大的结点数为2^i-1

　　深度为k的二叉树的最大结点数为2^k-1

　　对于非空二叉树, 叶结点个数 = 度为2的非叶结点个数 + 1

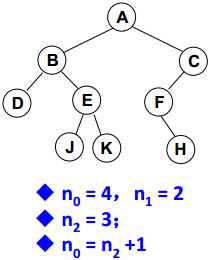
　　证明方式为: 对于非空二叉树, 存在度为0, 1 ,2的结点, 个数分别记为n0, n1, n2

　　根据 边=所有点-1=n0 + n1 +n2 -1

　　同时度为0, 1, 2的结点分别提供了0, 1, 2条边

　　因此 边 = 0*n0 + 1*n1 + 2*n2

　　得到 n0 + n1 +n2 -1 = 0*n0 + 1*n1 + 2*n2

　　(4) 二叉树的抽象数据类型定义

　　最重要的操作方法是遍历

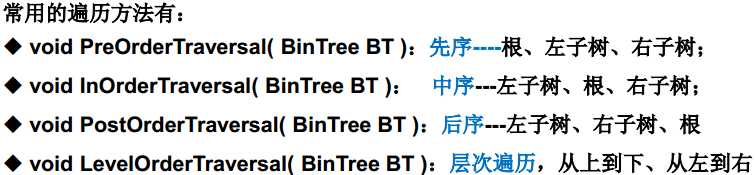
2.2 二叉树的存储结构

　　(1) 顺序存储结构

　　可以用数组存储完全二叉树

　　完全二叉树: 按从上到下, 从左到右顺序存储n个结点的完全二叉树的结点父子关系　

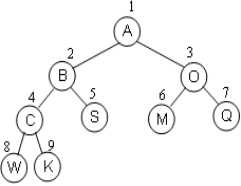
　　存储为

　　同时可以通过计算得到一个结点的父亲节点, 左孩子, 右孩子

　　　　父亲节点是[i/2]向下取整

　　　　左孩子是 2i

　　　　右孩子是 2i+1

　　但是如果一般的二叉树采用这样的方式存储的话, 需要填充一部分不存在的元素, 因此会造成很大程度上的空间浪费

　　(2) 链表存储

3 二叉树的遍历

　　二叉树一般还是使用链式存储, 二叉树的遍历是基于链式存储的二叉树来的

　　(1) 

Mooc数据结构-03树

标签：解决   完全   操作方法   事物   链式   二叉树   排列   管理   str   

原文地址：http://www.cnblogs.com/weihuchao/p/6933601.html