机器学习-Probabilistic interpretation

标签：存在   部分   推导   均值   lin   选择   解释   log   src   

Probabilistic interpretation，概率解释 
解释为何线性回归的损失函数会选择最小二乘 

 表示误差，表示unmodeled因素或随机噪声，真实的y和预测出来的值之间是会有误差的，因为我们不可能考虑到所有的影响结果的因素，比如前面的例子，我们根据面积和卧室的个数来预测房屋的价格，但是影响房屋价格的因素其实很多，而且有很多随机因素，比如买卖双方的心情，而根据中心极限定理，大量独立的随机变量的平均值是符合正态分布或高斯分布的 
所以这里对于由大量unmodeled因素导致的误差的分布，我们假设也符合高斯分布。因为你想想，大量独立随机变量大部分误差会互相抵消掉，而出现大量变量行为相似造成较大误差的概率是很小的。
  
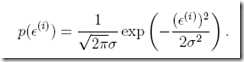
可以写成，因为误差的概率和预测出是真实值的概率是一样的 
  
注意，这里：
  
不同于 ：
 
表示这里θ不是一个随机变量，而是翻译成  因为对于训练集，θ是客观存在的，只是当前还不确定，所以有：
 
这个很容易理解，真实值应该是以预测值为中心的一个正态分布，给出θ似然性的定义：
  
给定训练集X和参数θ，预测结果等于真正结果的概率，等同于该θ为真实θ的可能性（似然性）。这里probability和likelihood有什么不同，答案没有什么不同。但是对于数据使用probability，对于参数使用likelihood，故最大似然法（maximum likelihood），就是找出L(θ)最大的那个θ，即概率分布最fit训练集的那个θ。

继续推导，把上面的式子带入，得到 
 

实际为了数学计算方便，引入log likelihood， 
 

可以看到，最终我们从L(θ)的最大似然估计，推导出损失函数J(θ)，最小二乘法：

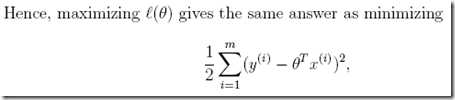
所以结论为，最小二乘回归被认为是进行最大似然估计的一个很自然的方法 。

机器学习-Probabilistic interpretation

标签：存在   部分   推导   均值   lin   选择   解释   log   src   

原文地址：http://www.cnblogs.com/sirius-swu/p/6936896.html