IP lookup is one of the key functions of routers for packets forwarding and classifying. Generally, IP lookup can be simplified as a Longest Prefix Matching (LPM) problem. That‘s to find the longest prefix in the Forwarding Information Base (FIB) that matches the input packet‘s destination address, and then output the corresponding Next Hop information.
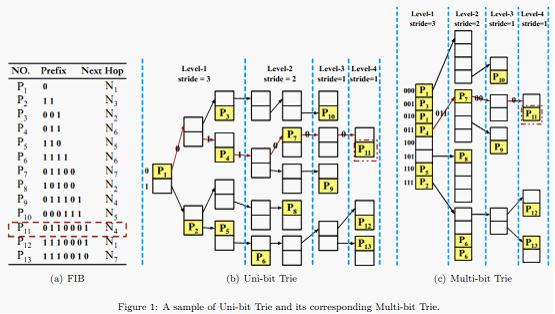
Trie-based solution is the most wildly used one to solve LPM. As shown in Fig.1(b), an uni-bit trie is just a binary tree. Processing LPM on it needs only traversing it from the root to some leaf, according to the input packet‘s destination address. The longest prefix along this traversing path is the matched one. In order to reduce the memory accesses for one lookup, we can compress some consecutively levels of the Uni-bit Trie into one level, transforming the Uni-bit Trie into a Multi-bit Trie.
For example, suppose the strides array is {3, 2, 1, 1}, then we can transform the Uni-bit Trie shown in Fig.1(b) into a Multi-bit Trie as shown in Fig.1(c). During the transforming process, some prefixes must be expanded. Such as 11(P2), since the first stride is 3, it should be expanded to 110(P2) and 111(P2). But 110(P5) is already exist in the FIB, so we only store the longer one 110(P5).
Multi-bit Trie can obviously reduce the tree level, but the problem is how to build a Multi-bit Trie with the minimal memory consumption (the number of memory units). As shown in Fig.1, the Uni-bit Trie has 23 nodes and consumes 46 memory units in total, while the Multi-bit Trie has 12 nodes and consumes 38 memory units in total.
The first line is an integer T, which is the number of testing cases.
The first line of each case contains one integer L, which means the number of levels in the Uni-bit Trie.
Following L lines indicate the nodes in each level of the Uni-bit Trie.
Since only 64 bits of an IPv6 address is used for forwarding, a Uni-bit Trie has maximal 64 levels. Moreover, we suppose that the stride for each level of a Multi-bit Trie must be less than or equal to 20.
Output the minimal possible memory units consumed by the corresponding Multi-bit Trie.
38
题意:题目大意,给了一个数列,N个数,要求将数列分成多段,每段长度不能超过20,那么由公式sum( a[i]*2^(l) ) (a[i]表示每一段的第一个数值,l表示这一段的长) 得到一个值,要求输出将数列分割后最小的值。
思路:区间DP,定义dp[i]表示从i到数列尾的子数列的值,那么可以得到状态转移方程,dp[i]=min( dp[i] , dp[j]+(1<<(j-i)) ) ( j>i &&j-i<=20)
代码如下:
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
using namespace std;
typedef long long LL;
LL a[100];
LL dp[100];
int main()
{
int T,N;
cin>>T;
while(T--)
{
scanf("%d",&N);
for(int i=1;i<=N;i++) scanf("%lld",&a[i]);
for(int i=1;i<=N;i++) dp[i]=19999999999999999;
dp[N+1]=0;
for(int i=N;i>=1;i--)
{
for(int j=i+1;j-i<=20&&j<=N+1;j++)
{
dp[i]=min(dp[i],dp[j]+a[i]*(LL)(1<<(j-i)));
}
}
printf("%lld\n",dp[1]);
}
return 0;
}
