标签:round sig names sum code swa size sign else
又到了神奇的模拟赛时间~
真是丧~
好吧我们来看看题目
小红帽是Pop star上最著名的人类画家,她可以将任何画出的东西变成真实的物品。赋予她这样神奇能力的正是她手上的画笔。
小红帽每次作画时,都需要用到她的调色盘,我们把每个自然数都对应一种颜色,那么小红帽的调色盘就可以看成是一个斐波那契数列(数列第1、2项都为1),小红帽每次需要一种颜色时,她都会用画笔蘸取一段区间,得到的颜色就是区间里所有的数之和。
受到秋之国人民的邀请,小红帽要为他们画一个夏天。小红帽要进行n次取色,给出每次蘸取的区间[l,r],作为小C委派来进行记录的你需要输出每次小红帽得到的颜色,答案对mod取模。
【数据范围】
对于10%的数据,n<=100,l,r<=10^4;
对于30%的数据,l,r<=10^7;
对于90%的数据,mod<=10^9;
对于100%的数据,0<=n<=1000,1<=l<=r<=10^18,0<mod<=10^18。
————————————————我是分割线————————————————————
很显然,这道题目就是求斐波那契数列前r项的前缀和减去前l-1项的前缀和,普通的DP都可以做到求斐波那契数列,但是很显然10^18我们就会T
在此我们讲讲矩阵乘法
矩阵乘法,顾名思义,就是2个矩阵相乘。具体如下
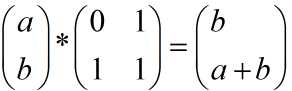
所以呢我们如果要算斐波那契数列的第N项只需要将图中的 矩阵自乘n-2次,再乘第一个矩阵,得到的矩阵的第一个数就是答案
矩阵自乘n-2次,再乘第一个矩阵,得到的矩阵的第一个数就是答案
那么我们又怎样求前缀和呢?
在此有两种方法供参考
TOP1:找规律
我们假设a,b为斐波那契数列的第一项和第二项
那么我们很显然就可以递推出后面的几项

那么这有什么规律呢?
很快就发现了规律
a=a+b-b;a+b=a+2b-b;2a+2b=2a+3b-b;3a+4b=3a+5b-b.....
所以我们只需要求num[r+2]-1-(num[l-1+r]-1)=num[r+2]-num[l-1]即可啦
TOP2:构造矩阵
显然我们知道我们要保留答案矩阵的前面2个数,而我们想办法构造出第三个数,用于计算前缀和。这样将这个矩阵自乘n-2次,输出第三个数就好啦。
然后我们会想到我们的前缀和就是sum[i]=sum[i-1]+num[i];
然后就会构造出这个矩阵啦
———————————————我是分割线—————————————————
那么我们还看到一个问题,如何处理mod?
我们知道如果mod为10^18
那么一次乘法操作的数会达到10^36
如果是这样我们就需要做高精除+高精乘了。
但是有没有更快的方法?
首先我们知道如果在加法中进行取余,结果不改变。
所以我们将乘法转变为加法
这样速度虽然慢了点,却不会爆long long
然后这道题就愉快解决啦!
下面贴代码
#include<cstdio> #include<cstring> #include<algorithm> using namespace std; int n; struct matrix{ unsigned long long mat[2][2]; }; unsigned long long l,r,mod; long long mul(long long x,long long y) { if (x<y) swap(x,y); register long long z=0; for (;y;y>>=1,x<<=1,x=x>=mod?x-mod:x) if (y&1) z+=x,z=z>=mod?z-mod:z; return z; } matrix multiply(matrix a,matrix b) { unsigned long long sum=0; matrix c; memset(c.mat,0,sizeof(c.mat)); for(int i=0;i<=1;i++) for(int j=0;j<=1;j++) { sum=0; for(int k=0;k<=1;k++) { long long numqq=mul(a.mat[i][k],b.mat[k][j]); if(mod>1000000000)sum+=numqq,sum%=mod; else sum+=(a.mat[i][k]*b.mat[k][j])%mod; } c.mat[i][j]=sum; } return c; } matrix matmod(matrix a,unsigned long long k) { matrix res; memset(res.mat,0,sizeof(res.mat)); for(int i=0;i<=1;i++)res.mat[i][i]=1; while(k) { if(k&1)res=multiply(res,a); k>>=1; a=multiply(a,a); } return res; } unsigned long long work(unsigned long long x) { if(x==0)return 0; if(x==1)return 1; if(x==2)return 2; matrix a,b; memset(a.mat,0,sizeof(a.mat)); memset(b.mat,0,sizeof(b.mat)); for(int i=0;i<=1;i++)a.mat[i][1]=1; for(int i=0;i<=1;i++)b.mat[i][0]=1; a.mat[1][0]=1; a=matmod(a,x); a=multiply(a,b); return (a.mat[1][0]-1+mod)%mod; } int main(){ freopen("artist.in","r",stdin); freopen("artist.out","w",stdout); scanf("%d%lld",&n,&mod); for(int i=1;i<=n;i++) { scanf("%lld%lld",&l,&r); unsigned long long num1=0,num2=0; num1=work(l-1); num2=work(r); unsigned long long ans=num2-num1+mod; printf("%lld\n",ans%mod); } return 0; fclose(stdin); fclose(stdout); }
标签:round sig names sum code swa size sign else
原文地址:http://www.cnblogs.com/ghostfly233/p/6937411.html